Tobby_And_Friends's blog

Prime Gap
By Tobby_And_Friends, history, 8 years ago, In English

How to determine whether a number is a product of consecutive primes? The number can be at max 10^14. Any hints is really appreciated.

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +13 Vote: I do not like it

If the number is a product of 2 consecutive primes then how large can those primes be?
What is the maximum number of consecutive primes you can multiply so that the product is within 10^14?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Assume p and q are the required consecutive primes which satisfy p*q=n. Since p is not equal to q, p has to be less than √n and q has to be greater than √n. Also, for them to be consecutive, p has to be the largest prime number less than √n and q has to be the smallest prime number greater than √n.

Edit: The above solution checks for 2 consecutive primes. The above solution extended for k primes is explained here.

→ Reply
»
8 years ago, # |
← Rev. 8   Vote: I like it +10 Vote: I do not like it

If you are only looking for 2 consecutive primes, then find the largest prime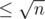 and the smallest prime 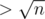and check if their product is equal to n. You might be able to make a similar idea work for any number of consecutive primes, though it seems tricky.

If it's a variable number of consecutive primes, you can try to binary search for a k-size subarray of primes that matches, for k ≥ 2. Note that k < 13 https://oeis.org/A002110. You would also have to check is n is prime.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If there is only one query, you can find all primes in [2, 107], find the smallest prime that divides N and check the product easily. Be careful when N is a prime number.

→ Reply