SkyDec's blog

HackerRank 101Hack 43rd Edition
By SkyDec, history, 8 years ago, In English

Hello Codeforces community!

I am glad to announce that HackerRank 101 Hack 43rd edition will be held on 17th Nov 2016 at 16:30 UTC. You can sign up for the contest here. Though what's priceless is solving interesting problems and the thrill of competition, prizes make the competition fierce. Top 10 performers will get a HackerRank T-shirt.

Problems have been set by SkyDec and tested by wanbo. The contest will consist of 5 problems with variable scoring distribution. You’ll have 120 minutes to solve them. We have tried our best to prepare a nice problem set. Hopefully everyone will enjoy. Also, you'll be able to enjoy the detailed editorials written by the setter.

If anyone are interested in sharing their knowledge, you can comment in this post or send message to wanbo. We eagerly need bunch of good problems.

Good luck and have fun!

  • Vote: I like it
  • +28
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by SkyDec (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Would the problems be in English ?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

in K-inversions do you mean k <= nC2 as well as nc2 <= 1e5 or k <= nc2 and k <= 1e5

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +46 Vote: I do not like it

AC solution on Maximal And-Or Product


int main(){
    int n;
    cin >> n;
    vector  <int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    sort(a.rbegin(), a.rend());
    int t = min(n, 5000);
    long long ans = 0;
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < min(n, i + 5000); j++) {
            ans = max(ans, (a[i] | a[j]) * (long long) (a[i] & a[j]));
        }
    }
    cout << ans << '\n';
    return 0;
}
→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +24 Vote: I do not like it

    just checking i and i + 1 works too

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      At Maximal And-Or Product,Just the | and & of the largest 2 different number should solve it :D

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      That's just because of weak testcases.
      Here's an anti test case for sorting and then taking max of every a[i] and a[i+1].
      4
      1 8 16 65

      → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it -33 Vote: I do not like it

    Yeah,the editorial is overcomplicated,there is an easy brute:

    AC
    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +26 Vote: I do not like it

    the solution with just two maximal numbers gets 100%, that's fine.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    By the editorial we can prove that we only need to consider the top log(a_i) number。 We didn't find it before contest. I'm very sorry.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it -13 Vote: I do not like it

    My solution : 

    cin>>n;
    cin>>arr[1];
    mx = arr[1];

    for(int i=2; i<=n; i++){
        cin>>arr[i];
        ans = max(ans, ll((arr[i]&mx)*(arr[i]|mx)));
        mx = max(mx, arr[i]);
    }

    cout<<ans<<endl;
    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +18 Vote: I do not like it

Full score in D — sort the array and while we have time, take two random indices greater than N-1000 and compare their f to the answer.

WTF, taking only the 2 largest numbers gives full score, too. Simple counter-example is {1, 1, 2^27, 2^28}, the answer is 1.

→ Reply
»
8 years ago, # |
  Vote: I like it +40 Vote: I do not like it

Problem E

→ Reply
»
8 years ago, # |
  Vote: I like it +45 Vote: I do not like it

1) Last problem was similar to https://www.hackerearth.com/problem/algorithm/perfect-permutations-september-clash/description/

2) Tests for this problem are weak, my O((k - n)2) solution passed

→ Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it +5 Vote: I do not like it

(nevermind)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain the approach in editorial for Problem D? Thanks!

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +21 Vote: I do not like it

    For the j-th bit and for set S,you partition numbers in 2 sets. S0-those who have j-th bit set to 0, S1-those who have j-th bit set to 1. Let's call the answer for j-th bit and set S f(S,j).

    Now we got three cases:

    • If cardinal of any of them is 0, our answer will surely take only numbers from one set. So there is no need to make the choice now, we will make it later and apply same algorithm for (j-1)-th bit. So we call f(S,j-1).

    • |S1| = 1 and the rest are in S0. Now the answer could be in S0 or the x in S1 and some number in S0. Let's brute-force through all y in S0, relax the answer with (x&y)*(x|y), then call f(S0,j-1).

    • |S1| > 1. This needs some observation. It's better from now on to choose only numbers from S1. Why? Because choosing 2 numbers with j-th bit 1 would make the answer have the 2*j-th bit 1 at least, which is the best and cannot be done with other 2 numbers in S. So we will make the choice later and call f(S1, j-1).

    You can see that we actually relax the answer in step2, but it's not necessarily to go there for some input(ex. all numbers are equal). You got to be careful. Also 2nd step is done at most log times. When I say we make the choice later, it's something like f(S,j) = F(S',j-1).

    For a better intuition of why it works, it's like excluding at every step some numbers we surely know it won't give the best answer,if that's the case. The key was to make the observation at 3rd step.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 4   Vote: I like it +20 Vote: I do not like it

      For the third case, where |S1| 1, there is a mistake in the proof.

      Choosing a number from |S1| and a number from |S0| may result in a number with 2 * j - th bit equal to 1. E.g. 111, 011 (Read as binary numbers of course).

      The following is a correct proof:

      Let the current bit is j.

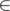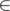      We want to disprove that there exists some x, z, y, such that x S1, z S1, y 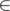S0, and f(x, y) f(x, z).

      Well, it's obvious that for an arbitrary x, f(x, y) is maximized when y  =  2j - 1. And also f(x, z) is minimized when z  =  2j. Hence, it's sufficient to just disprove this case.

      Let a be x - 2j. Then:

      → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Nevermind (got it finally).

→ Reply