Приветствую всех участников раунда!
203A - Two Problems
Из-за совсем небольших ограничений можно было перебрать минуту, на которой Вася пошлет решение по первой задаче и минуту, на которой Вася пошлет решение второй задачи. Однако были несколько хитрых случаев: нужно было не забыть, что Вася может послать только одну задачу (то есть в этом случае нужно было перебрать только одну величину), а также может вообще не посылать задачи — в этом случае он получает 0 баллов.
203B - Game on Paper
В этой задаче очевидно следующее тривиальное решение: после каждого хода нужно проверить, не появилось ли черного квадрата со стороной 3 на поле, но ограничения не позволяют так решать задачу. Однако заметим, что как только Вася закрашивает некоторую точку (x, y), то требуется проверить лишь 9 возможных кандидатов на черный квадрат, а остальные квадраты со стороной 3 не поменяют своей раскраски.
Таким образом, решение работает за O(m) с константой порядка 80 и требует O(n2) памяти.
203C - Photographer
Заметим, что если Вася хочет обслужить клиента номер i, то ему понадобится ровно f(i) = a·xi + b·yi мегабайт памяти на фотоаппарате. Также заметим, что так, как мы хотим максимизировать количество клиентов, то гораздо выгоднее брать тех, у кого величина f(i) меньше. Таким образом мы приходим к решению: сразу при чтении данных запомним для каждого клиента величину f(i), отсортируем всех клиентов по этой величине и будем обслуживать в порядке возрастания до тех пор, пока хватает памяти в фотоаппарате.
Время работы — O(n·log(n)).
203D - Hit Ball
Эта задача имеет два разных решения.
Решение 1. Будем последовательно двигаться по траектории мяча до тех пор, пока не влетим в поверхность двери. Для этого будем считать от каждой точки следующую точку, где текущий луч пересекает какое-либо препятствие (стена, дверь и так далее). Каждая точка на луче имеет вид (x + t·vx, y + t·vy, z + t·vz), где t > 0 — параметр. Подставим уравнения всех препятствий в этот вид и найдем минимальное t, а значит, и точку, где луч пересечет препятствие первый раз. Осталось только пересчитать vx, vy,vz и повторить процесс дальше до тех пор, пока мяч не влетит в дверь. Пересчитывать компоненты вектора скорости очень просто — при столкновении соотвествующую компоненту нужно просто умножить на - 1.
Время работы такого решения — O(X2), где X — максимальная из координат мяча в начальный момент времени.
Решение 2. Как известно, траекторию отражения луча света от зеркала можно считать прямой, если отразить относительно зеркала все остальные объекты. Для уточнения приведем рисунок: на нем можно построить траекторию движения луча от точки A к точке B отразив точку в B в B' и нарисовав отрезок AB’.

Аналогичную идею будем использовать в нашем решении. Каждую координату x или z будем находить независимо, рассмотрим для x, для z аналогично.
Допустим у нас нет стен, тогда мяч прилетел бы в точку с координатой 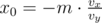 . Теперь допустим x0 > 0, а стена представляет собой прямую x = a. Тогда мысленно отразим наш коридор (то есть полосу между прямыми x = 0 и x = a) несколько раз, то есть получим множество прямых x = ka, где пространство между соседними прямыми — это одно из отражений коридора.
. Теперь допустим x0 > 0, а стена представляет собой прямую x = a. Тогда мысленно отразим наш коридор (то есть полосу между прямыми x = 0 и x = a) несколько раз, то есть получим множество прямых x = ka, где пространство между соседними прямыми — это одно из отражений коридора.
Посмотрим, сколько раз отрезок между точками (a / 2, m) и (x0, 0) пересекал прямые, и в зависимости от четности можно понять, от какой стороны коридора последний раз отразился мяч, прежде чем попал в дверь. А сам ответ несложно найти отложив величину x0 (mod a) (где "mod" означает остаток от деления нацело) от соответствующей стены.
Таким образом, описанное решение позволяет найти ответ за O(1).
203E - Transportation
В этой задаче требуется рассмотреть два случая.
Первый — пусть все роботы едут самостоятельно. Тогда выделим множество роботов, у которых li ≥ d, отсортируем их по возрастанию количества требуемого горючего, и будем брать в этом порядке и отправлять в багажное отделение пока не кончится топливо. Этот случай похож на решение задачи C этого же раунда.
Второй случай рассматривает тех роботов, которые вкладывают друг в друга. Выделим множество роботов, у которых ci > 0, пусть из всего k штук, и пусть 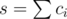 . Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь
. Тогда несложно понять, что если мы всех этих роботов упакуем так, чтобы лишь 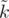 из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется
из них ехало самостоятельно, а остальные были вложены в другие роботы, то еще у нас останется 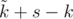 свободных слотов для других роботов.
свободных слотов для других роботов.
Таким образом, выделим множество роботов у которых ci > 0, li ≥ d — то есть эти те роботы, которые могут везти других роботов и при этом могут самостоятельно добраться до багажного отделения.
Переберем, сколько из таких роботов на самом деле поедут своим ходом (не забываем про ограничения на топливо), и по формуле выше найдем количество свободных слотов. Заметим, что мы уже в любом случае отправили всех роботов, у которых ci > 0, а значит остались только те, у которых ci = 0, пусть таких всего num.
Каждый робот может иметь 3 состояния: он займет один из слотов, он поедет своим ходом, если у него li ≥ d и если хватит топлива, или он вообще не поедет.
Известно, сколько имеется слотов, а значит можно найти, сколько роботов или поедут своим ходом, или останутся, а точнее их 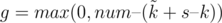 . Таким образом, нам надо найти среди всех роботов с ci = 0 и li ≥ d максимальное количество роботов (но не более, чем g штук), на которых осталось достаточно топлива. Остальные роботы поедут на свободных слотах или останутся (их известное количество).
. Таким образом, нам надо найти среди всех роботов с ci = 0 и li ≥ d максимальное количество роботов (но не более, чем g штук), на которых осталось достаточно топлива. Остальные роботы поедут на свободных слотах или останутся (их известное количество).
Эта подзадача решается предподсчетом величины f(i), означающую минимальное количество топлива, необходимое чтобы отправить i роботов среди тех, для которых выполняется ci = 0 и li ≥ d. По этой функции, очевидно, можно делать бинарный поиск.
Таким образом, соберем элементы решения: сначала переберем количество роботов, которые поедут своим ходом среди тех, у которых ci > 0, а затем с помощью бинарного поиска по предподсчитанной величине найдем, сколько роботов из оставшихся уместятся на свободные слоты, сколько поедут также своим ходом, а сколько останутся.
Не забудем про случай, когда вообще все роботы едут самостоятельно.
Мы получаем алгоритм, который можно реализовать за время O(n·log(n)).











В задаче про мяч не возникнет проблемы при ударе об стык потолка/стены? По идее из-за точности можно придумать тест когда он не туда попадает.
В условии было сказано, что мяч — материальная точка.
Можно считать, что вначале он отскакивает от стены, а потом (проделав нулевой путь) от пола, или наоборот.
В правке тупость.. неправильно понял ограничения.
Ну это же 9 миллиардов, как оно поместится?
по-моему,это решение за 9*1000*1000*m работает...
Откуда в D берется асимптотика O(X^2)?
тест: 1 1 N N -1 0
между двумя точками отражения по координате Y расстояние около 1 / N, а значит расстояние N преодолевается за N2 шагов
А, ну да, действительно — vy здесь больше равно единицы=)
Я чуть-чуть по-другому решил B:
Запоминаем когда закрасили каждый квадрат и потом обрабатываем все квадраты 3 на 3:
n = 4
m = 15
0 — квадрат не закрашен
X — квадрат закрашен на X ходу
Здесь у нас 2 возможных квадрата (остальные 2 откидываем)
Осталось всего-лишь выбрать в каждом из этих квадратов максимальные числа ( в первом 15, во втором 11), а из этих максимальных минимальное — оно и будет ответом :) В данном случае 11.
Сложность — O(n^2), если не учитывать константу 9 :)
UPD Извиняюсь за такой толстый пост :)
Круто придумал.
Спасибо :)
В 203E - Перевозки оказалось очень удобно сделать для роботов, у которых li < d, значение fi = INF...
И никто даже не заметил, что Валеру из контеста подменили каким-то Васей о_о
Никак не удается сдать задачу Е.
Идея такова. Рассмотрим два случая.
1) Все роботы добираются самостоятельно. Для этого сортируем роботов, которые могут доехать, по увеличению затрат бензина, жадно набираем ответ.
2) Какие-то роботы добираются на других. Выберем робота, которая может доехать, и при этом тратит наименьшее количество бензина. Очевидно, что все роботы, для которых c!=0, смогут доехать на нем до финиша. Теперь посмотрим на роботов, у которых с==0. Пусть cnt1(первый тип) из них не могут добраться самостоятельно(l[i]<d), cnt2 — могут. Пускай у нас осталось еще can мест. Тогда наберем на эти места роботов первого типа. Роботов второго типа посортируем по затратам бензина. Если у нас еще остались свободные места после набора роботов первого типа, то посадим на них роботов, которые едят больше всего бензина, остальных же попробуем жадно заставить ехать самих.
Такое решение получает wrong answer на 13-ом тесте. Вот посылка. Подскажите пожалуйста, что не так в этой идее.
не всегда выгодно, чтобы все роботы с ci > 0 вкладывались в одного. Иногда нужно сделать так, чтобы несколько таких роботов ехало своим ходом, так как это увеличивает число свободных мест.
В разборе это число называется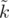 .
.
А почему так получается? Посмотрим на какого-то робота, которого мы грузим на другого робота, с c[i]>0. Он заберет себе 1 место, и добавит c[i] мест. Так как c[i]>=1, то мы ничего не ухудшили,а как минимум оставили столько же свободных мест, сколько и было до его погрузки.
не совсем.
Из всех роботов с ci > 0 только внешние (назовем их так) не занимают места. Значит, чем больше внешних — тем больше места.
Да, я понял, спасибо.
Все еще не удается сдать задачу Е. Вроде бы все делаю как в разборе + пробовал тестить на большом количестве рандомных тестов и сравнивать ответы с решением, которое получило Accepted — все сходится. Вот посылка, подскажите пожалуйста, что не так
Если все еще интересно, то вот тест:
Правильный ответ 16 20
Все еще интересно:) Спасибо.