is it true that  ?
?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 148 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/17/2025 03:48:59 (f1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Just thoughts.
L is left part, R is right part.
L = PL1 + PL2 + ... + PLk
R = PR1 + PR2 + ... + PRk
My theory is for all i = 1..k PLi > PRi.
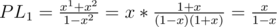
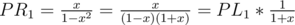
Induction. Base i = 1.
So for x > 0: PL1 > PR1
And I really don't know what's next (if I'm on the right path).
Yeah, it is true. But proving this is a bit painful. Here is the only way I know:
Reminder: generating function of sequence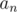 is formal series
is formal series  .
.
Consider amount of ways to split number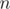 in sum of distinct numbers. Generating function for this sequence is
in sum of distinct numbers. Generating function for this sequence is 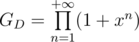 . Now consider number of ways to split number
. Now consider number of ways to split number 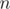 in sum of not necessary distinct odd numbers. Generating function for this sequence is
in sum of not necessary distinct odd numbers. Generating function for this sequence is 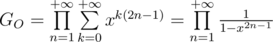 . Let's multiply each functions by
. Let's multiply each functions by 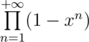 . Then first one becomes
. Then first one becomes 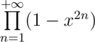 and the second one become
and the second one become 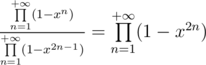 . Thus number of ways to split
. Thus number of ways to split 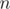 in distinct numbers equals number of ways to split in in odd numbers (you can also prove it with some combinatorics, I guess).
in distinct numbers equals number of ways to split in in odd numbers (you can also prove it with some combinatorics, I guess).
Now consider which is the number of ways to split
which is the number of ways to split 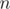 in
in 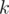 distinct numbers.
distinct numbers. 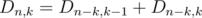 . Thus if
. Thus if  then
then 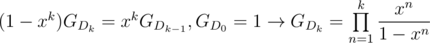 . Then
. Then 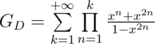 .
.
And with odd numbers part we have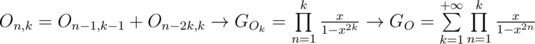 . Since
. Since 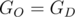 , we have equation from the statement now.
, we have equation from the statement now.
Understanding of correctness of each transition in proof is left to reader as an excercise ;)