Недавно, решая задачи Петрозаводских тренировок этого года, столкнулся с интересной задачей:
есть массив, размера N < = 105, и три типа запросов:
1 l r d -- увиличить все элементы на отрезке от l до r на t
2 l r -- на отрезке применить операцию взятия корня в округлением вниз, т.е. 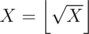
3 l r -- почитать сумму на отрезке.
Запросов так же до 105, X всегде меньше 105
Пробовал разные подходы, но ничего работающего не нашел.
Подскажите, может кто знает.
З.Ы. Не хочет вставлять формулы :( Очень странный редактор постов











Auto comment: topic has been translated by DeWitt (original revision, translated revision, compare)
А какое ограничение на x?
До 10^5
По логике вещей, если проталкивать в ДО второй запрос до тех пор, пока на отрезке, соответствующему вершине, не будут все числа равны, то суммарно это будет работать не более чем за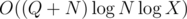 . Но ни мне, ни моему сокоманднику не удалось пропихнуть это в ТЛ (валится на 102-ом тесте).
. Но ни мне, ни моему сокоманднику не удалось пропихнуть это в ТЛ (валится на 102-ом тесте).
А вообще, можно ж видео разбора посмотреть, и не гадать, как ее решать)
З.Ы.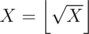
доллар X = \left \lfloor \sqrt{X} \right \rfloor долларНа контесте такое решение заходило (например, мы сдали). После контеста был придуман и добавлен контртест (кажется, как раз номер 102). Тест такой:
Можно заметить, что числа будут ходить по циклу 3 -> 15 -> 3 и 4 -> 16 -> 4, то есть на каждый запрос можно обойти всё дерево.
Однако после контеста мы смогли это обойти :) Не помню, как именно, но суть сводилась к тому, что надо ифать не тогда, когда остался один элемент на всём отрезке, а когда два очень близких.
Could you share the problem link?
Ignore: this one has interval adding
https://official.contest.yandex.ru/uacamp-online-2016/contest/2872/problems/H4/ I'm not sure whether you are able to enter the contest, so the statement:
I found almost the same problem in hdoj.
http://acm.split.hdu.edu.cn/showproblem.php?pid=5828
However,the author's solution can't pass all tests after data enhancement.I found most accepted solution before data enhancement used this way:
1.build a segtree to store the sum,maximum and minimum value in an interval.
2.increase and get sum operation equals to normal segtree operations.
3.In an interval,if maximum value equals to the minimum value,the sqrt operation only covers interval by the same value.
4.If sqrt(maximum)-sqrt(minimum)==1 ,the sqrt operation equals to subtraction operation.
5.If sqrt(maximum)-sqrt(minimum)==0 ,the sqrt operation equals to interval cover.
6.else just recursion down.Due to the number of times need to get a number sqrted to 1 is small,the efficient is not too slow.
Here is one of the code passed before data enhancement.
/*****************************************************/
You forgot to mention that for step 4 we need maximum == minimum + 1
Auto comment: topic has been updated by DeWitt (previous revision, new revision, compare).
Автокомментарий: текст был обновлен пользователем DeWitt (предыдущая версия, новая версия, сравнить).