Всем привет!
В Самаре 14 апреля прошел сабж, а теперь мы хотим провести тренировку на Codeforces на этих задачах. Тренировка пройдет 11 июня в 11:00, благо, у россиян это выходной. Длительность контеста — 5 часов. Приглашаем всех принять участие!
Контест завершился, поздравляем maksay с победой и с пропихом самой сложной задачи контеста; теперь мы уменьшили на нее ограничения, и пропих, скорее всего, больше не удастся :)
Виртуальное участие тут: http://codeforces.me/gymRegistration/100052/virtual/true
Ссылка на тренировку: http://codeforces.me/gym/100052
Осторожно, в комментах спойлеры!
Контест готовили: I_love_natalia, steiner, pank.dm, Shlakoblock, elena и Александр Ефимов, которого нет на CF.
Особенности:
- Задачи доступны только на русском языке, но не исключено, что в будущем будет перевод.
- Сложность контеста выставлена 4 звезды, но на самом деле он немного полегче, где-то 3.5 звезды.
- Автор текстов условий — elena (зачем я это пишу? Просто примите участие в контесте!)
- Для ввода-вывода используются файлы input.txt и output.txt
- Как всегда, не надо использовать %lld, если сдаете решения на GNU C++
контест командный?
В оригинале был командный.
У тех, кто работает по пятидневке.
Хороший контест, но за условия авторов хочется отправить в "the special hell" (c)
Какое было авторское решение задачи С? Жадность или паросоч? Моя печенка говорит мне, что и паросоч тут выполняется где-то за O(N * log3N + N2), но строго доказать не получается.
Диванные рассуждения привели меня к честному потоку. В левой доле — вторая тетрадь, в правой — первая. Изначально граф, как при паросочетании Объединим одинаковые вершины в правой доле. Теперь из каждой вершины левой доли не более 8 ребёр. Найдём поток за O(FE) = O(N·8N) = O(N2).
Решение было таким.
Построим граф в 4 "слоя". На первом слое будут вершины второй половины инпута, на каждом следующем слое — вершины, отличающиеся от вершин предыдущего слоя наличием звездочки в одной из позиций, где на предыдущем слое звездочки не было. Например, на первом слое
abc, на втором —*bc,a*c,ab*, на третьем —**c,*b*,a**, на четвертом, последнем слое — всегда одна вершина***.Между вершинами соседних слоев, отличающихся ровно в одной позиции, проведем ребра бесконечной пропускной способности.
Из вершин первого слоя (они соответствуют второй половине инпута) проведем ребра в сток, такой пропускной способности, сколько таких строчек во второй половине инпута.
Из истока проведем ребра в вершины, соответствующие строчкам из первой половины инпута, такой пропускной способности, сколько таких строчек в первой половине инпута.
Находим поток, вычисляем соответствия. На Java работает 1.5 секунды.
Да, действительно, по-человечески) А у меня во время контеста были эзотерические рассуждения о том, что если рассматривать записи как точки в 3Д, то любая вершина паросочетается с выпуклым множеством точек. (В данном случае вообще — точкой, прямой, плоскостью или всем пространством). В случае 1Д это, во-1, позволяет решить задачу жадно, а во-2 позволяет паросочу работать за O(N * logN), по крайней мере мне вроде кто-то так говорил). Ну и навскидку в 3Д получается куб при логарифме.
Похоже, даже 4 секунды ТЛа — это многовато, потому что жадность перед паросочем (да еще если посортировать сначала по возрастанию количества *), сочетает процентов 80% вершин.
Я хотел написать жадность, а Hohol меня остановил, сказав, что первая итерация Куна построит то же самое, что сделает жадность — его убивать надо, получается? Вершинки мы как только не сортили, в ТЛ не укладывались.
Не ври, через некоторое время на контесте я сказал, что был неправ, и ты написал что хотел.
Хм, в лучшем нашем сабмите этого куска кода нет... Я его так и не написал, получается? Жалко.
мы добрые
Хм.. видимо, это зависит от реализации. У е-макса сказано, что играет, видимо, потому что каждый раз очищается массив юздов — и просто построить тест, где у и-той вершины чередующаяся цепь длины и. Я немного по-другому пишу (ближе к тому, что за (N2logN), хотя и что-то среднее) и у меня это идентично, а жадность я выношу в отдельный блок скорее по привычке.
UPD: бррр.. Первая итерация Куна? В том, что у е-макса, каждая итерация строит +1 чередующуюся цепь. Может все-таки вы тоже кодили что-то другое, где каждый раз проходишься по всем еще не паросочтенным и пробуешь построить цепь от них? (Это, по-моему, не Кун, хотя я давно запутался в терминологии. А то, что он венгр, только усложняет ситуацию:) )
Видимо, речь идет о реализации, которая чистит visit только по необходимости (т.е. когда DFS ничего не нашел). Там действительно похоже, что первая итерация ищет начальную жадность.
У нас вроде так и было...
Утверждается, что в жадном случае вида "вводимо отношение порядка в доле" Кун работает за N*log(N) (если только не будет квадрата на генерации графа)?
Да, мне когда-то очень давно казалось такое говорили. Но по здравом размышлении — мне кажется, что это бред. К примеру, на тесте, где вершина И паросочетается с промежутком [1..N + 1 - i].
В то же время, если вводимо отношение порядка, то все отрезки действительно можно посортировать по левому концу, при равном левом по возрастанию правого и действовать жадно.
Возможно, вот в таком случае и правда будет N*log(N) в среднем (не получается доказать оценку, пока):
Пусть двудольный граф построен по принципу a[i] < b[j], причем a и b — случайные. Пусть граф задан списком соседей для каждой вершины, причем этот список в случайном порядке. Будем оценивать только время работы Куна.
Upd. Интуиция говорит, что мы в каждой вершинке, проходя ее, в среднем будем приближаться к жадному ответу в два раза.
Такие условия — традиция самарских олимпиад. Тем более, что это приближает олимпиады по программированию к промышленному "угадай, что имел ввиду заказчик" :)
А если серьезно, то знаем, что это одно из самых слабых мест. Будем работать в этом направлении.
Давай-ка сразу скажем, что это традиция олимпиад в СамГУ. Вот на этом контесте условия были вменяемые, по крайней мере ни одного клара не было)
У вас просто нетрадиционная олимпиада.
Да, кстати. Я несколько раз думал о том, чтобы дать задачу, подобную Д, но меня всегда останавливал известный факт что:
а
. И то и другое можно трактовать как "с равной вероятностью в любую точку круга", только в разных системах координат.
Я прав или какую мне надо подучить матчасть?
Мне казалось, что "с равной вероятностью в любую точку круга" это стандартная двумерная мера "площадь", нормированная на площадь круга, например, на Борелевской сигма-алгебре, и в таких задачах система координат не имеет значения. Я не прав?
Я рассуждал так: нам надо найти матожидание величины g((x, y)) = x2 + y2. (В задаче нам это было не надо, но посчитаем среднее значение расстояния от любой точки круга до центра). Распределение абсолютно непрерывное? Вроде да. По определению матожидание функции от АНСВ это
. Исходя из фразы "с равной вероятностью в любую точку" — f(x) = const. ω — поверхность единичного круга. Я прохожу все точки единичного круга двойным интегралом в одной и в другой системе координат, получаю две разных величины. Не прав, видимо, я, но я не вижу где.
Ну мне кажется, что при переходе от одной системы кордина в другую надо не забывать домножать на якобиан. В нашем случаи он просто r
Детально по этой задаче — руками ответ считал в полярных координатах, а на контесте развлекался, пытаясь затолкать метод Монте-Карло. Затолкать не получилось, но исключительно из-за точности, четыре (относительных) знака у меня сходилось.
Ну, я тоже делал, только не Монте-Карло, а проход сеткой. И вот: http://ideone.com/otiU3
А, я понял. Ты упорно пытаешься игнорировать ρ якобиана при переходе к полярным координатам.
Да, точно, вот та самая матчасть которую надо подучить. Сенкс)
Формулы очень сложно читать.
φ
\varphi\int\limits_0^1\int\limits_0^{2\pi}{r^2\cdot(cos^2(\varphi)+sin^2(\varphi))}d\varphi drЕще видимо во второй формуле ошибка, потому что cos2 + sin2 = 1, и он как-то странно смотрится в формуле.Чушь написал.Ну да. Для всех полярных углов-то расстояния интеграл по расстоянию дает одно и то же значение, центральная симметрия. Так что можно заменить на просто:
Формулы сейчас подправлю, спасибо.
Если простым языком, то твои разные ответы соответствуют разной плотности вероятности по точкам. Во втором случае вероятность попадания в круг радиуса 0.01 у центра больше чем вероятность попадания в круг радиуса 0.01 у края, потому что сначала равновероятно распределяется полярный угол точки, а потом её модуль. В первом же случае вероятность попадания в какую-нибудь область будет строго пропорциональна площади этой области.
А можно я задам какой-нибудь глупый вопрос. Разве написав внешний интеграл ровно так, мы не сказали, что попадание во все x/r равновероятно, что неверно.
Да, это именно то, что я упустил — что в сферических координатах перебираемые мной точки расположены не равномерно относительно кусочков площади, в которых они находятся.
Это то я понял. Я пока не понимаю, почему первый правильный. Во первых там точно не хватает коэффициента
, который площадь круга. Видимо то что мне хочется куда-то дописать ровно его и создаст.
Вроде, ответ первого интеграла PI/2, второго 2*PI/3.
Я пока в упор не понимаю, почему первый, это не "случайным образом равномерно выбрали x, при фиксированным x равномерно выбрали y".
Видимо то что я имею ввиду, это
UPD. Спасибо Zlobober. На эти 2 корня, надо не только домножить, но и поделить.
Да, пардон, естественно ответ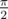
, я просто машинально записал числа которые посчитал кодом, уже с делением.
Где можно разбор посмотреть?
Разбора нет (во всяком случае, я о нем не знаю), задавайте вопросы, вам ответят.
Окей.
В задаче Е у меня была такая идея: посчитать количество инверсий в исходной перестановке, а затем сдвигать перестановку на элемент влево. Тогда к количеству инверсий прибавится величина, зависящая лишь от этого самого первого числа (допустим, х): n — x — (x — 1). Неправильный ответ на тесте 12. Где я не прав\как решать?
Задача G — пробовал сортировать дни, рыцарей, всё что угодно — всё не то. Как решать?
Задача K — перебор? Как красивее написать?
Задача L — ???
E — именно так и делается. Где-то ошибка в реализации. Вот мое: http://pastebin.com/JErMY7k0. Еще можно деревом Фенвика решать...
E — решение правильное. Скорее всего реализация.
G — Рыцарей имеет смысл приглашать в порядке увеличения M. Доказывается от противного. Если не так, то поменяли, стало не хуже. Дальше динамика по (день, рыцарь).
K — Да, перебор. Просто перебираем куда поставить очередной палец. Если еще перебирать и устройство, то случается TL. Поэтому надо понять, что его надо поставить всегда, причем на самый низкий лад куда можно. реализация.
L — Задачу можно сформулировать так. Появляются и удаляются числа, найти наибольшую сумму с не очень большим max — min. Задачи (update в точке + запрос на отрезке) и (update на отрезке, запрос в точке) более-мене эквивалентны. Для обратимых операций типа суммы точно. Будем добавлять не точку, а отрезок на который она повлияла. Тогда надо просто найти максимум. Прибавление на отрезке + максимум = дерево отрезков.
Проблема в том, что в тренировках не видно посылок, если ты не сдал задачу. Иначе я бы не спрашивал, а просто посмотрел бы код.
К — можно динамика F(лад, ставили ли мы что-то на предыдущий) = максимальное число оставшихся пальцев. На текущий либо ставим пальцы либо баррэ либо пропускаем если ничего ставить не надо.
K — у меня еще проще.
Для каждого лада посчитаем, сколько нужно пальцев, чтобы "разобраться" с ним (если на этом ладу ничего не надо нажимать — 0, если можно зажать все с помощью баррэ — 1, иначе — число струн, которые необходимо зажать на этом ладу). По этим данным можно легко определить, какое минимальное необходимое количество пальцев для всего аккорда. Если их надо не больше 4 — ответ YES, иначе — NO. Устройство ставим в самую нижнюю возможную позицию — поэтому отбрасываем крайнее ненулевое значение. Понятно, что все остальные будут входить в ответ — суммируем их; к ответу надо так же прибавить количество "разрывов" (т.е. количество серий из 0, которые находятся между группами из положительных значений) — для преодоления каждого такого разрыва нам нужен 1 палец (который не будет зажимать ничего и позволит следующему пальцу "перепрыгнуть" разрыв в один или несколько ладов).
По вашему коду у меня осталось ощущение, что сжатие заодно делает перестановку обратной. И если на число инверсией это не влияет, то циклические сдвиги обратной в терминах прямой, это какая-то ересь.
Да, действительно. Спасибо!
А как D решается?
Тут выше обсуждалось — надо посчитать матожидание расстояния между 2 случайными точками круга (D) и матожидание расстояния от дракона до случайной точки круга (L). Ответ L + (n — 1) * D в силу линейности матожидания. Грубо ответ можно приблизить перебором пар точек круга, или посчитать интеграл по поверхности круга, только, как обсуждалось выше — по Х и У.
Без подсчета интегралов — еще можно заметить, что D = D(r), L = L(r, xD, yD). Ну и еще что D = D(1) * r * r, L = L(xD / r, yD / r) * r * r. После этого сначала посчитать грубо и увидеть D(1) = 1. После этого поиграться с xD, yD и увидеть, что L(1, xD, yD) = xD * xD + yD * yD + 0.5
Финальная формула ответа — xD * xD + yD * yD + (n — 1 + 0.5) * r * r. Ее также можно получить посчитав 2 интеграла.
Поймём, чему равно матожидание квадрата длины из точки A(x0, y0) в случайную точку B(x, y) круга радиуса R. Оно по линейности матожидания есть M[(x — x0)^2] + M[(y — y0)^2] = x0^2 + y0^2 + M[x^2 + y^2] + 2x0 M[x] + 2y0 M[y]. M[x] = M[y] = 0 по симметрии относительно нуля. Значит осталось научиться считать M[x^2 + y^2]. M[x^2 + y^2] =
(потом что относительная вероятность попадания на окружность радиуса r — 2π r, а значение функции на этой окружности — r), что есть 1/2. Теперь поймём, что для двух случайных точек квадрат разности расстояния между ними как раз и выходит R2. Поэтому ответ — x02 + y02 + (2N - 1)R2 / 2.
UPD: не успел.
Для центра и случайной —
. Для двух случайных все же вдвое больше.
Да, точно.