A reminder that AtCoder doesn't only have Grand Contests, but also these. Starting time: in the past.
Also post-contest discussion, I guess.

| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
A reminder that AtCoder doesn't only have Grand Contests, but also these. Starting time: in the past.
Also post-contest discussion, I guess.

| Name |
|---|



クマ means "bears".
Is there going to be an editorial (in English) for this contest unlike the previous regular contest?
Well, this was easy. Stupid MLE on the last problem... btw the main part of my solution was computing L-tuples of balanced sequences of parentheses with N - L parentheses in total (L = |S|). That's a L-tuple convolution of one array with itself, which can be computed in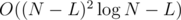 in the same way as fast exponentiation, since convolution is associative.
in the same way as fast exponentiation, since convolution is associative.
Yes, the last problem of last ARC was exceptionally hard but usually ARC tends to be easy. Anyway, you can predict the difficulties from point values.
It may also be solved in O(n2). Let
dp[n][l]= number of ways to get lengthlafternkeystrokes. Now answer isdp[n][l] / 2^lwithl = s.size()since all strings of same length are equviprobableIt's seems that it's a solution from editorial (I've found 2^m and O(n^2) in it) but I'm not sure.
Yes, this is intended.
And now we can add FFT and get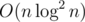 solution.
solution.
Anyway, the intended O(n2) solution much more beatiful.
Indeed.
Recently, I think a lot in terms of convolutions and solving the last problem with FFT. It's probably connected to FFT problems becoming much more common recently.
I "solved" it in different way. First observe that the answer depends only on N and L = |S|. Then write O(N3) brute-force and display results for N, L ≤ 10. Look at these values and observe that:
f[i][i] = 1
f[i][j] = f[i - 1][j - 1] + 2 * f[i - 1][j + 1].
f[i][j] = f[i][j - 1] if i = j(mod2).
Precompute f[1][N] for N = 1, 2, ..., 5000 with brute-force and include those values in your code (I searched for the sequence in OEIS but failed). Then just use observed formulas to fill the f[][] table.
Can someone please explain dp approach to last problem.. I didnt get the part that all strings were equiprobable..thus I was trying an alternate dp state..dp[i][j]->denotes that we have made i moves and have got string of length j which matches first j characters of input string(basically a prefix of length j)..however I couln't figure out the transitions.
Can someone help me with ARC 59 — E?