zscoder's blog

RMQ with "Push Update"
By zscoder, history, 8 years ago, In English

Recently I encountered a problem which is very similar to RMQ.

Abridged Statement : First, you have an empty array. You have two operations :

  1. Insert a value v between positions x - 1 and x (1 ≤ x ≤ k + 1) where k is the current size of the array.(positions are 1-indexed)

  2. Find the maximum in the range [l, r] (i.e. the maximum from the positions l to r inclusive)

There are at most Q ≤ 250000 queries.

My current solution uses SQRT decomposition but it was not fast enough to get AC. I was wondering if there is an 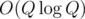or 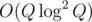solution.

Edit : Forgot to mention that the queries must be answered online (it's actually function call), so offline solutions doesn't work.

  • Vote: I like it
  • +26
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Click

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Sounds like a common use of implicit treap. Here is some information about it — http://e-maxx.ru/algo/treap (I know it's in Russian but I don't know Russian and I learnt it from there with google translate). Also this code helped me a lot — https://sites.google.com/site/indy256/algo_cpp/treap :) And I am pretty sure I have solved a similar problem on SPOJ but I can't find it right now. I will post my code whenever I find it :)

UPD: Now I see that I have solved http://www.spoj.com/problems/HORRIBLE/ this way just to try it :D Here is my code — http://ideone.com/vQtdmN. I have implemented push, range-sum and range-update queries but for range-max the idea is pretty much the same. And yeah, my code is based on indy256's implementation.

→ Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Deleted.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

https://threads-iiith.quora.com/Treaps-One-Tree-to-Rule-em-all-Part-1
https://threads-iiith.quora.com/Treaps-One-Tree-to-Rule-em-all-Part-2

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Where can I find this problem? A link to the testing system would be appreciated.

→ Reply
»
8 years ago, # |
← Rev. 20   Vote: I like it +5 Vote: I do not like it

ignore

→ Reply
»
8 years ago, # |
  Vote: I like it +46 Vote: I do not like it

There is also a nice trick how to convert a problem that deals with insertions in off-line into a standard RMQ problem.

If you known the resulting sequence beforehand, you would just build a segment tree and simply answer all queries (replacing the elements that didn't appear yet with  - ∞). The only problem is to build mapping from indices at arbitrary moment of time t into indices in the resulting sequence.

Let's process queries starting from the last one. Consider the last insertion query. Suppose it was on position p. You definitely know that this element stays on position p in the final sequence. Also you know that for queries before if you meet a position q ≥ p then it actually maps into at least position q + 1 because there will be one more element to the left of it in the future.

This can be formally described as a following process: keep a segment tree with 0's and 1's and sum operation. Zeroes mean the positions in the final sequences that are not assigned yet, and ones mean the positions that were already used. Process the insertion queries starting from the last one. Whenever you see the query "insert number x at the position p", you have to find the p-th zero from the left, and you can easily do that by one query on the segment tree.

So, by keeping this auxillary segment tree you can map positions in the sequence at any arbitrary time into positions in the final sequence, so you can store your minimums in the segment tree and answer for all queries in .

This may sound harder than just storing a sequence in a rope-like structure, like an implicit treap, but this solution is way faster since we heavily exploit the offline nature of the problem by using only segment trees that are much more efficient.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    "You have to find the p-th zero from the left, and you can easily do that by one query on the segment tree." Can someone explain how this can be done using only one query? I am thinking of doing this in terms of binary search (with query on segment tree).

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Store sums in a segment tree. Invert the meaning of 0's and 1's. Now you have to find the p-th 1, that is the same as the first position such that the sum on its prefix is greater or equal to p. Look at the root vertex, you have two options: if its left subtree sum is greater or equal to p, then the desired position is definitely in the subtree of the left child of the root, move there. Otherwise you have to find (p - leftsum)-th 1 in the subtree of the right child of the root, move there.

      This results in a simple procedure working in .

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        can someone give me some problem about this trick,or implemented code? thanks.

        → Reply
»
8 years ago, # |
← Rev. 5   Vote: I like it -8 Vote: I do not like it

Hi all.

First get all queries and find the final array and save all indexes of numbers for each inserting query.

Make a new array with size of the last one and make all of its elements -INF.

Make a segment tree on this new array and for each inserting query update the index of this query (in the final array) to the number.

& for each asking query call segment_tree_getmax(l , r);

==>O(QlgQ)

thanks.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How do you find the final array in O(QlgQ)? It seems you have to use some data structure or the approach I described above.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    online solution!

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +13 Vote: I do not like it

      He had already posted his comment when zscoder added to the blog that he needs an online solution.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).

→ Reply