Обсуждение контеста
Задача A. Проблема Нольдбаха
В данной задаче нужно было уметь искать простые числа в диапазоне от 2 до N. При этом ограничения позволяли искать их любым способом - как решетом Эратосфена, так и перебором всех возможных делителей числа.
Возьмём каждую пару соседних простых чисел и проверим, является ли их сумма, увеличенная на 1, простым числом. Найдём количество таких пар, сравним с числом K и выведем ответ.
Задача B. Иерархия
Заметим, что если у каждого человека, кроме одного, будет ровно один начальник, то полученная иерархия будет древовидной.
Рассмотрим для каждого человека все заявления, в которых он фигурирует как подчинённый. Если более чем для одного человека таких заявлений не существует вообще, очевидно, что ответ -1. В противном случае, найдём минимальную стоимость такого заявления для каждого человека и сложим эти стоимости. Это и будет ответ.
Также можно было применить алгоритм Крускала для нахождения минимального остовного дерева в графе. Однако перед добавлением каждого ребра в дерево необходимо добавить проверку того, что ни у одного сотрудника не появится больше одного начальника.
И да, значения квалификаций сотрудников не были нужны для того, чтобы решить задачу :)
Понятие квалификации вводилось для того, чтобы обеспечить отсутствие циклов.
Задача C. Баланс
Рассмотрим входную строку A длиной n. Проделаем некоторые операции из условия над этой строкой; допустим, мы получили строку B. Сжатием строки X будем называть такую строку X’, полученную из X путём замены всех подряд идущих одинаковых букв на одну такую же букву. Например, для строки S = “aabcccbbaa”, её сжатие S’ = “abcba”.
Рассмотрим сжатия строк A и B - A’ и B’. Можно заметить, что если строку B можно получить из строки A через некоторые операции из условия, то B’ является подпоследовательностью A', и наоборот - если для любых строк A и B равной длины B' является подпоследовательностью A', то строку B можно получить из строки A через некоторые операции из условия.
Интуитивно это можно обосновать так. Допустим, мы использовали какую-то букву a на позиции i в строке A для того, чтобы расставить букву a на позициях j..k строки B (путём использования операций из условия). Тогда мы не могли использовать буквы на позициях в строке A, меньших i, для того, чтобы каким-то образом повлиять на буквы k + 1..n строки B; аналогично, мы не могли использовать буквы на позициях в строке A, больших i, для того, чтобы повлиять на буквы 1..j - 1 строки B.
Теперь у нас есть некоторая основа для нашего решения, которое будет заключаться в применении динамического программирования. Будем составлять строку B посимвольно, учитывая тот факт, что сжатие B' должно оставаться подпоследовательностью сжатия A' (попутно с составлением B будем искать сжатие B' в A'). Для этого будем хранить позицию i в строке A', означающую, на какой позиции остановился поиск B' в A', и три параметра kA, kB, kC, означающие соответственно размер множества каждой из букв a, b, c в строке B. Переходы в этом рекуррентном соотношении следующие:
1) Следующий символ строки B - это a. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'a', kA + 1, kB, kC).
2) Следующий символ строки B - это b. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'b', kA, kB + 1, kC).
3) Следующий символ строки B - это c. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'c', kA, kB, kC + 1).
Здесь nexti, x - это минимальное такое j, что j ≥ i и A'j = x (то есть ближайшее, начиная с позиции i, вхождение символа x в A'). Естественно, если для какого-то случая значение nexti, x не определено, то переход невозможен.
Подсчитав рекуррентную функцию f(i, kA, kB, kC), ответ найти несложно: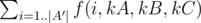 для всех троек kA, kB, kC, для которых выполняется условие сбалансированности.
для всех троек kA, kB, kC, для которых выполняется условие сбалансированности.
Такое решение не укладывается в ограничение по памяти и по времени. Заметим, что если строка B собирается быть сбалансированной, то должно выполняться условие kA, kB, kC ≤ (n + 2) / 3. Таким образом, количество состояний в рекуррентном соотношении уменьшилось приблизительно в 27 раз. Однако можно ещё в несколько раз уменьшить количество используемой памяти, если заметить, что во всех переходах значение kA (для этой цели можно взять и kB, и kC) изменяется либо на 0, либо на 1. Значит, можно хранить матрицу значений f по слоям (где слой задаётся некоторым значением kA).
Сложность решения O(N4) с достаточно маленькой скрытой константой.
Задача D. Блокнот
Ответ на задачу равен bn - 1 * (b - 1) mod c. Главное, что нужно уметь делать в этой задаче - считать значение AB mod C для некоторых длинных чисел A и B и короткого числа C. Простой алгоритм быстрого возведения в степень не проходит ограничение по времени по той причине, что для того, чтобы перевести число B в двоичную систему, потребуется порядка O(|B|2) операций, где |B| - количество цифр в десятичной записи числа B.
Первое, что нужно сделать - превратить A в A mod C. Несложно понять, что такое преобразование не меняет ответ.
Представим C в виде C = p1k1p2k2...pmkm, где pi - различные простые числа.
Посчитаем ti = AB mod piki для всех i следующим образом. Здесь есть два случая:
1) A mod pi не равно 0: тогда A и pi взаимно просты, и можно применить теорему Эйлера: AB' = AB (mod C), где B' = B mod φ(C), а φ(C) - это функция Эйлера;
2) A mod pi равно 0: тогда при B ≥ ki будет выполняться ti = AB mod piki = 0, а при B < ki можно тривиально посчитать это значение.
Так как все piki попарно взаимно просты, то можно применить китайскую теорему об остатках для подсчёта результата.
Также можно применить теорему Эйлера напрямую. Заметим, что для некоторых B1, B2 ≥ 29 выполняется |B1 - B2| mod φ(C) = 0, то все значения ti для них будут совпадать (29 - это максимальное возможное значение ki). Используя это, можно уменьшить число B до относительно небольших размеров и посчитать ответ алгоритмом быстрого возведения в степень.
Есть ещё одно решение, применявшееся многими участниками. Представим число B в виде B = d0 + 10d1 + 102d2 + ... + 10mdm, где 0 ≤ di ≤ 9 (фактически di - это i-я с конца цифра числа B). Так как ax + y = ax· ay, получаем, что AB = Ad0· A10d1· ...· A10mdm. Значения A10i можно узнать последовательным возведением в степень 10; зная A10i, можно узнать и A10idi возведением первого в степень di. Ответ - произведение всех множителей (разумеется, по модулю C).
Задача E. Палисечение
Первое, что нужно сделать - найти все подпалиндромы в заданной строке. Для этого можно применить красивый алгоритм, описанный на сайте e-maxx.ru/algo. Вкратце, результатом работы этого алгоритма являются максимальные возможные длины подпалиндромов, центры которых находятся либо в позиции i строки, либо между позициями i и i + 1, для всех таких возможных позиций центра.
Для примера, предположим, что максимальная длина подпалиндрома с центром в позиции i равна 5; это значит, что центр в позиции i находится у трёх подпалиндромов: длины 1 (i..i), 3 (i - 1..i + 1) и 5 (i - 2..i + 2). Получаем, что все возможные начала подпалиндромов лежат на отрезке i - 2..i. В общем случае начала и концы подпалиндромов с фиксированным центром будут занимать некоторый отрезок позиций, который можно легко найти.
Найдём для каждой позиции i строки величину starti, равную количеству подпалиндромов, начало которых находится в позиции i. Все эти значения можно найти за линейное время. Для этого заведём вспомогательный массив ai. Если после обработки некоторой позиции выяснилось, что какие-то новые подпалиндромы начинаются в позициях i..j, то значение ai увеличим на 1, а значение aj + 1 уменьшим на 1. Теперь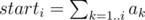 . Обоснование этого факта оставляется читателю в качестве упражнения :)
. Обоснование этого факта оставляется читателю в качестве упражнения :)
Аналогичным образом можно вычислить finishi - количество подпалиндромов, конец которых находится в позиции i.
Так как можно несложно подсчитать общее количество подпалиндромов, найдём количество пар непересекающихся подпалиндромов и вычтем это количество из общего количества пар. Заметим, что если два подпалиндрома не пересекаются, то один из них лежит в строке строго левее другого. Количество пар непересекающихся подпалиндромов можно подсчитать по формуле:
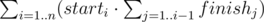
Эту сумму можно найти за линейное время, если значение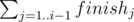 при переходе от i к i + 1 пересчитывать добавлением finishi к уже накопленной сумме.
при переходе от i к i + 1 пересчитывать добавлением finishi к уже накопленной сумме.
Таким образом, сложность решения O(N).
Задача A. Проблема Нольдбаха
В данной задаче нужно было уметь искать простые числа в диапазоне от 2 до N. При этом ограничения позволяли искать их любым способом - как решетом Эратосфена, так и перебором всех возможных делителей числа.
Возьмём каждую пару соседних простых чисел и проверим, является ли их сумма, увеличенная на 1, простым числом. Найдём количество таких пар, сравним с числом K и выведем ответ.
Задача B. Иерархия
Заметим, что если у каждого человека, кроме одного, будет ровно один начальник, то полученная иерархия будет древовидной.
Рассмотрим для каждого человека все заявления, в которых он фигурирует как подчинённый. Если более чем для одного человека таких заявлений не существует вообще, очевидно, что ответ -1. В противном случае, найдём минимальную стоимость такого заявления для каждого человека и сложим эти стоимости. Это и будет ответ.
Также можно было применить алгоритм Крускала для нахождения минимального остовного дерева в графе. Однако перед добавлением каждого ребра в дерево необходимо добавить проверку того, что ни у одного сотрудника не появится больше одного начальника.
И да, значения квалификаций сотрудников не были нужны для того, чтобы решить задачу :)
Понятие квалификации вводилось для того, чтобы обеспечить отсутствие циклов.
Задача C. Баланс
Рассмотрим входную строку A длиной n. Проделаем некоторые операции из условия над этой строкой; допустим, мы получили строку B. Сжатием строки X будем называть такую строку X’, полученную из X путём замены всех подряд идущих одинаковых букв на одну такую же букву. Например, для строки S = “aabcccbbaa”, её сжатие S’ = “abcba”.
Рассмотрим сжатия строк A и B - A’ и B’. Можно заметить, что если строку B можно получить из строки A через некоторые операции из условия, то B’ является подпоследовательностью A', и наоборот - если для любых строк A и B равной длины B' является подпоследовательностью A', то строку B можно получить из строки A через некоторые операции из условия.
Интуитивно это можно обосновать так. Допустим, мы использовали какую-то букву a на позиции i в строке A для того, чтобы расставить букву a на позициях j..k строки B (путём использования операций из условия). Тогда мы не могли использовать буквы на позициях в строке A, меньших i, для того, чтобы каким-то образом повлиять на буквы k + 1..n строки B; аналогично, мы не могли использовать буквы на позициях в строке A, больших i, для того, чтобы повлиять на буквы 1..j - 1 строки B.
Теперь у нас есть некоторая основа для нашего решения, которое будет заключаться в применении динамического программирования. Будем составлять строку B посимвольно, учитывая тот факт, что сжатие B' должно оставаться подпоследовательностью сжатия A' (попутно с составлением B будем искать сжатие B' в A'). Для этого будем хранить позицию i в строке A', означающую, на какой позиции остановился поиск B' в A', и три параметра kA, kB, kC, означающие соответственно размер множества каждой из букв a, b, c в строке B. Переходы в этом рекуррентном соотношении следующие:
1) Следующий символ строки B - это a. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'a', kA + 1, kB, kC).
2) Следующий символ строки B - это b. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'b', kA, kB + 1, kC).
3) Следующий символ строки B - это c. Тогда переход произойдёт из состояния (i, kA, kB, kC) в (nexti, 'c', kA, kB, kC + 1).
Здесь nexti, x - это минимальное такое j, что j ≥ i и A'j = x (то есть ближайшее, начиная с позиции i, вхождение символа x в A'). Естественно, если для какого-то случая значение nexti, x не определено, то переход невозможен.
Подсчитав рекуррентную функцию f(i, kA, kB, kC), ответ найти несложно:
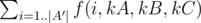 для всех троек kA, kB, kC, для которых выполняется условие сбалансированности.
для всех троек kA, kB, kC, для которых выполняется условие сбалансированности.Такое решение не укладывается в ограничение по памяти и по времени. Заметим, что если строка B собирается быть сбалансированной, то должно выполняться условие kA, kB, kC ≤ (n + 2) / 3. Таким образом, количество состояний в рекуррентном соотношении уменьшилось приблизительно в 27 раз. Однако можно ещё в несколько раз уменьшить количество используемой памяти, если заметить, что во всех переходах значение kA (для этой цели можно взять и kB, и kC) изменяется либо на 0, либо на 1. Значит, можно хранить матрицу значений f по слоям (где слой задаётся некоторым значением kA).
Сложность решения O(N4) с достаточно маленькой скрытой константой.
Задача D. Блокнот
Ответ на задачу равен bn - 1 * (b - 1) mod c. Главное, что нужно уметь делать в этой задаче - считать значение AB mod C для некоторых длинных чисел A и B и короткого числа C. Простой алгоритм быстрого возведения в степень не проходит ограничение по времени по той причине, что для того, чтобы перевести число B в двоичную систему, потребуется порядка O(|B|2) операций, где |B| - количество цифр в десятичной записи числа B.
Первое, что нужно сделать - превратить A в A mod C. Несложно понять, что такое преобразование не меняет ответ.
Представим C в виде C = p1k1p2k2...pmkm, где pi - различные простые числа.
Посчитаем ti = AB mod piki для всех i следующим образом. Здесь есть два случая:
1) A mod pi не равно 0: тогда A и pi взаимно просты, и можно применить теорему Эйлера: AB' = AB (mod C), где B' = B mod φ(C), а φ(C) - это функция Эйлера;
2) A mod pi равно 0: тогда при B ≥ ki будет выполняться ti = AB mod piki = 0, а при B < ki можно тривиально посчитать это значение.
Так как все piki попарно взаимно просты, то можно применить китайскую теорему об остатках для подсчёта результата.
Также можно применить теорему Эйлера напрямую. Заметим, что для некоторых B1, B2 ≥ 29 выполняется |B1 - B2| mod φ(C) = 0, то все значения ti для них будут совпадать (29 - это максимальное возможное значение ki). Используя это, можно уменьшить число B до относительно небольших размеров и посчитать ответ алгоритмом быстрого возведения в степень.
Есть ещё одно решение, применявшееся многими участниками. Представим число B в виде B = d0 + 10d1 + 102d2 + ... + 10mdm, где 0 ≤ di ≤ 9 (фактически di - это i-я с конца цифра числа B). Так как ax + y = ax· ay, получаем, что AB = Ad0· A10d1· ...· A10mdm. Значения A10i можно узнать последовательным возведением в степень 10; зная A10i, можно узнать и A10idi возведением первого в степень di. Ответ - произведение всех множителей (разумеется, по модулю C).
Задача E. Палисечение
Первое, что нужно сделать - найти все подпалиндромы в заданной строке. Для этого можно применить красивый алгоритм, описанный на сайте e-maxx.ru/algo. Вкратце, результатом работы этого алгоритма являются максимальные возможные длины подпалиндромов, центры которых находятся либо в позиции i строки, либо между позициями i и i + 1, для всех таких возможных позиций центра.
Для примера, предположим, что максимальная длина подпалиндрома с центром в позиции i равна 5; это значит, что центр в позиции i находится у трёх подпалиндромов: длины 1 (i..i), 3 (i - 1..i + 1) и 5 (i - 2..i + 2). Получаем, что все возможные начала подпалиндромов лежат на отрезке i - 2..i. В общем случае начала и концы подпалиндромов с фиксированным центром будут занимать некоторый отрезок позиций, который можно легко найти.
Найдём для каждой позиции i строки величину starti, равную количеству подпалиндромов, начало которых находится в позиции i. Все эти значения можно найти за линейное время. Для этого заведём вспомогательный массив ai. Если после обработки некоторой позиции выяснилось, что какие-то новые подпалиндромы начинаются в позициях i..j, то значение ai увеличим на 1, а значение aj + 1 уменьшим на 1. Теперь
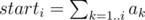 . Обоснование этого факта оставляется читателю в качестве упражнения :)
. Обоснование этого факта оставляется читателю в качестве упражнения :)Аналогичным образом можно вычислить finishi - количество подпалиндромов, конец которых находится в позиции i.
Так как можно несложно подсчитать общее количество подпалиндромов, найдём количество пар непересекающихся подпалиндромов и вычтем это количество из общего количества пар. Заметим, что если два подпалиндрома не пересекаются, то один из них лежит в строке строго левее другого. Количество пар непересекающихся подпалиндромов можно подсчитать по формуле:
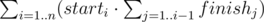
Эту сумму можно найти за линейное время, если значение
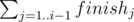 при переходе от i к i + 1 пересчитывать добавлением finishi к уже накопленной сумме.
при переходе от i к i + 1 пересчитывать добавлением finishi к уже накопленной сумме.Таким образом, сложность решения O(N).











По-моему, эта фраза это и обозначает, но всё же добавил пару слов.
Удалите, пожалуйста, лишние копии.
But what can you say about my solution?
In fact, it looks like:
a %= c;
p = phi(c);
ans = (a ^ (b % p)) % c;
if (b >= p && ((a ^ p) % c) == 0)
ans = 0;
Maybe there is some subtle counter-example?
Ah, of course, my bad memory :)
a %= c;
p = phi(c);
ans = (a ^ (b % p)) % c;
if (b >= p)
ans *= ((a ^ p) % c);
Can anyone explaine why does this solution work?
int[][][][] dp = new int[151][52][][];
for (int i = 0; i < dp.length; ++i) {
for (int j = 0; j < 52; ++j) {
dp[i][j] = new int[52 - j][];
for (int k = 0; j + k < 52; ++j) {
dp[i][j][k] = new int[52 - j - k];
}
}
}
This allocates only the elements actually needed by the solution, so fitting in memory limit.
C/C++ users may use "full" allocation - unused pages of memory will not be loaded, and ML will not be overcomed. But use it with care - there are some problems (not this one) using "lazy" dynamic programming where it is possible to load all or just too many pages by some tricky tests, even if the number of used cells is acceptable.
The tutorial is nice.
Will you post the tutorials for coming contests as well?
TEST24_E
#include "stdafx.h"
#pragma comment(linker, "/STACK:16777216")
#include <iostream>
using namespace std;
int main()
{
long n, q[1000], a[1000], b[1000], c[1000], m, min_st[1000];
int IsUch[1000], IsValid=0, i;
cin>>n;
for(i=0;i<n;i++)
{
cin>>q[i];
IsUch[i]=0;
min_st[i]=LONG_MAX-1;
}
cin>>m;
for(i=0;i<m;i++)
{
cin>>a[i]>>b[i]>>c[i];
if(q[a[i]-1]>q[b[i]-1])
{
IsUch[b[i]-1]=1;
min_st[b[i]-1]=min(min_st[b[i]-1], c[i]);
}
}
for(i=0;i<n;i++)
IsValid+=(IsUch[i]==0?1:0);
if(IsValid>1)
{
cout<<-1<<endl;
return 0;
}
long min_sum=0;
for(i=0;i<n;i++)
min_sum+=min_st[i]!=(LONG_MAX-1)?min_st[i]:0;
cout<<min_sum<<endl;
return 0;
}
Blog not visible tourist
Unable to parse markup [type=CF_HTML]
that was very nice catch that employee qualification was not necessary.. but it's tricky at the same time
=) I can't solve this =)