→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
10:47:48
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
10:47:48
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 06:47:13 (l1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Bumping. Hurry up to register.
This was a great contest! Although I am somewhat salty that I had a solution for the third problem in div2, here, http://ideone.com/172siu, but could not figure out how to submit it.
How to solve div1 600?
We can use Ax, y to denote whether circle y appears in the permutation x. Then the answer is . we can expand it.
. we can expand it.
We can choose k(1 ≤ k ≤ m) circles B1, B2...Bk, and let X be on of the permutations in which they all appear. Consider the trem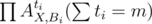 in the formula above, it's coefficient is
in the formula above, it's coefficient is 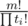 . We can find that
. We can find that  is equal to S(m, k) × k!. S(m, k) is the stirling number of the second kind. This formula only depends on the value of k.
is equal to S(m, k) × k!. S(m, k) is the stirling number of the second kind. This formula only depends on the value of k.
So we only need to calculate the number of each k appears, It is equal to |s(n + 1, k + 1)|. |s(n + 1, k + 1)| is the stirling number of the first kind. Because for each permutation of n + 1,if it has k + 1 circles, we can throw away the circle which includes n + 1 and then we get k circles. So for each k, we can easily calculate the devotion to the answer and we can solve this problem in O(tm + nm)
I have trouble seeing why number how many times each k appears is |s(n + 1, k + 1)|. More precisely what we want to compute is numbers of pairs (permutation P, k cycles inside it), so we probably want to construct a bijection between them and permutations of n+1 elements with k+1 cycles, but I fail to see that bijection from your description about throwing away last cycle.
Maybe I have not explained it well QAQ.
If we have chosen k disjoined circles, for each permutation which contains these circles, we can add a new position and use it to merge the other circles into a single circle.
If we have num permutations A1, A2, ...Anum to merge. We can sort them in the increasing order of the smallest id in the circle. And cut each circle before the smallest position and merge them in the order after sorting. Also, we can split any circle which contains n + 1 into some circles of 1 to n in an only way.
For example, when n = 5 and we have two circles (2, 4), (1, 5). After sorting, the order is (1, 5), (2, 4), and then we can merge them into (6, 5, 1, 4, 2).
And if we want to split a circle (6, 3, 5, 1, 2), we can easily split it into (3, 5, 1), (2).(Each time we can find the smallest number in the remaining sequence and cut it off, then we can restore the circles before merging).
So the occurrence times of each k is equal to the numbers of the permutation of length n + 1 which has k + 1 circles.
jiry_2 gave the bijection, but you don't actually need it.
Say you have n elements left after picking some cycles. The number of ways to complete the permutation with those n elements is n!. The number of ways to make a single cycle with those remaining elements and one extra element is n!. So those two numbers must count the same thing.
Of course, a bijection is then easy to construct: if the unpicked elements are a1, a2, ..., an take the cycle n + 1 -> x1 -> x2 -> ... -> n + 1 and turn it into a1 -> x1, a2 -> x2...
Ahh, tricky :).
Is there an easy slower solution to div1 600 I'm missing? I had (what I thought was a cool solution) that ran in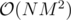 , but apparently the author only wanted the
, but apparently the author only wanted the 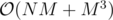 from Google.
from Google.
I came up with the O(NM2) solution immediately and stared at the input constraint like an idiot.
Okay, so today I learned that Stirling numbers of the first kind exist, and they are used to solve this exact problem. My solution that I thought was so cool is not cool anymore to me :(
I still think it's cool, but it changes nothing :(
Instead of computing the sum of s(n, k) * km, you can compute the sum of s(n, k) * comb(k, m). This will lead to an O(NM + QM) solution.
I wonder, is it a programming contest, a maths contest, or a googling contest???
Agreed. Div2 1000 was easily googleable, and was from an ASC!
And div1 Hard is similar to a problem by sevenkplus from a Chinese training contest in 2013. link
It's from IMO Shortlist 2005 C7: http://artofproblemsolving.com/community/c6h85076p494833
I was looking at Div 2 1000 after the contest, and after I read the problem, I was pretty damn sure I read the exact same problem before. ( that I couldn't solve : P )
With some googling, I found the exact same problem here : http://codeforces.me/gym/100221/attachments/download/1767/20052006-winter-petrozavodsk-camp-andrew-stankevich-contest-17-en.pdf
Please someone tell me it's different and there is something I can't get between them :D, otherwise how original? Seriously, that would really be a joke...
The TC problem includes square brackets. Having two different bracket types bumps the difficulty up a bit.
My solution to div1 600:
We want to calculate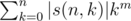 , where s(n, k) denotes Stirling numbers of the first kind.
, where s(n, k) denotes Stirling numbers of the first kind.
By using , where S(n, k) denotes Stirling numbers of the second kind, we just need to calculate
, where S(n, k) denotes Stirling numbers of the second kind, we just need to calculate 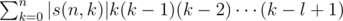 for all 0 ≤ l ≤ m.
for all 0 ≤ l ≤ m.
We know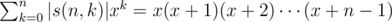 , and (xa)(b) = a(a - 1)(a - 2)... (a - b + 1)xa - b, where (xa)(b) denotes the m-th derivative of xa. So we just need to calculate (x(x + 1)(x + 2)... (x + n - 1))(l)x = 1, let u = x - 1, it becomes ((u + 1)(u + 2)(u + 3)... (u + n))(l)u = 0.
, and (xa)(b) = a(a - 1)(a - 2)... (a - b + 1)xa - b, where (xa)(b) denotes the m-th derivative of xa. So we just need to calculate (x(x + 1)(x + 2)... (x + n - 1))(l)x = 1, let u = x - 1, it becomes ((u + 1)(u + 2)(u + 3)... (u + n))(l)u = 0.
For convenience let f(u) = ((u + 1)(u + 2)(u + 3)... (u + n)). Consider Taylor's series at u = 0(Maclaurin's series), i.e.
We just need to expand f(u), and take the coefficient of xl, multiply it by l!. By the formula above we know it's |s(n + 1, l + 1)|.
Overall, the formula is:
BTW, you should be careful that n + 1 and m + 1 in the overall formula implies that you should calculate up to s(100001, 301). I knew this trick but I still made a tiny mistake which led to wrong answer when n = 100000 and m = 300. So sadly I had to resubmit and lost 100+ points :(
And you can see that there are many successful challenges based on this issue :)
Hello, I was a writer this time, it's my second round at topcoder. Thanks to cgy4ever for help in preparing problems.
Here's a short editorial and authors code:
div2-easy, TreeAndVertex
Answer is maximal degree. http://pastebin.com/K0nkNvbp
div2-medium, SegmentsAndPoints
Sort points and segements, then greedy. http://pastebin.com/FEu7WPpP
div2-hard, BracketSequenceDiv2
Dynamic programming: d[i][c] = number of non-empty sequences with balance i and last element c (c is '(' or ')'). Add one bracket and change d[i][c] accordingly.
http://pastebin.com/aiEwh1jV
div1-easy, BracketSequenceDiv1
O(2N / 2) meet-in-the-middle or O(n3) dynamic (d[i][j] number of cbs one can form using s[i:j]). The last is much easier to implement :) .
http://pastebin.com/mM9hi8hu
div1-medium, CyclesNumber
This problem is my personal favorite. Detailed solutions are explained in much detail by jiry_2 and matthew99 (btw, I used the same approach as matthew99 while creating problem).
Expected way to solve was something like this:
http://pastebin.com/m5BHKh64
div1-hard, XorPuzzle
Solution always exists, except case n = 2k and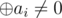 .
.
The way to find it is better explained by pseudocode:
Could you prove it works?
http://pastebin.com/9vQ2TMDi
I apologize for everyone who knew similar problems, hope you enjoyed the round anyway ^_^
Funny, it's the second time in a day I think that problemsetter's favorite problem is boring to solve. Goes to show setting problems and solving them is quite different.
Let's look at expected solution:
The second one looks even harder to count. Why would anyone transform the problem like this is beyond me (unless you were planning on taking combinations from the beginning, in which case you wouldn't take this step).
I agree the proof is short, but isn't it difficult to come up quickly with that result without knowing it beforehand? I'm pretty sure c(n+1, m+1) is not the first thing that came to my mind when looking at the sum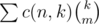 ...
...
So either you know the formulas and derivatives and Maclaurin series and whatnot, in which case it's doable, but mostly a mechanical problem, or you don't, and you need some unreasonable amount of divine inspiration to stand a chance of doing this in 50 minutes. Please don't pull off stuff like this again... u.u
In my case the process of solving this problem was a combination of searching some stuff in OEIS and trying to find patterns in sequences.
I think, it is matter of taste, mostly. I enjoy solving enumerative combinatorics problems, using generating functions or pure combinatorical reasoning (which is usually harder, but gives more satisfaction). I find it's really amazing. Hope there are more than a few people who likes it too.
Could you please suggest some books on enumerative combinatorics problems? I find them really interesting, even though I am not that good at them. Any kind of resources would be welcome. Thanks in advance. :)
About step from km to k(k - 1)...(k - m + 1) (and to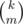 ). First counts m-tuples with repetitions, the second count m-typles without repetitions, which is more convinient in most cases. I thought it is more or less common trick.
). First counts m-tuples with repetitions, the second count m-typles without repetitions, which is more convinient in most cases. I thought it is more or less common trick.
Step from km to k(k - 1)...(k - m + 1) is not easy to come up with, but it definitely has a motivation behind it. If we look at a bigger picture, we are interested in computing some expressions Pm(k). If we look at formulas, we can see that in order to compute Pm(k) we need to get Pm - 1(k + 1). Unfortunately if we expand (k + 1)m we get a lot of terms, so we need our expression Pm(k) to be such that there is a nicer relation between Pm(k) and Pm(k + 1). Moreover Pm should also be a polynomial of degree m. Given this Pm(k) = k(k - 1)...(k - m + 1) looks like a very nice choice.
I haven't found out that by myself and I agree that it's hard to come up with it during a contest (especially such a short one as TC), I got to know that trick from problem D5 on recent Petrozavodsk camp, but I find it very nice and insightful :).
This explanation doesn't actually fit with Arterm's solution, which basically relied on knowing that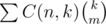 is easy to count as c(n + 1, m + 1).
is easy to count as c(n + 1, m + 1).
I assume you are talking about something similar to what cgy4ever gave then, which, while also involving some hard to figure out tricks (figuring out that the f function really does what we want it to do took me some time), is the only solution posted so far that doesn't use prior knowledge about Stirling numbers.
I agree with your conclusion -- it's a cool trick, but the fact that this solution isn't easy to come up with and that everyone else was using the Stirling formula solution makes it a bad fit for the contest format. Ideally, there shouldn't be problems for which uncommon/out-of-scope prior knowledge makes them significantly easier.
By the way, Petrozavodsk looks like a fun place, I wish I didn't live in the other side of the world :(
Hmm, actually I didn't expect many people can solve it in his way (If his solution is the only one I know, then that just can't be used as Div1-Medium) — and that is true, just few people solved it in that way.
So what went wrong is that no one solved it in the way I expect.
"Ideally, there shouldn't be problems for which uncommon/out-of-scope prior knowledge makes them significantly easier." — I totally agree with it. From my experience, this kind of 'math' problems usually have high risk to give some people big advantages: those who know advanced knowledge, or just good at play with formula.
Well, seems like we're all just saying the same thing with different words now. What I initially opposed was the formula solution being the expected, and you agree that is bad for a medium. So what happened is expected solution was harder than you thought, it must be difficult to judge and I hope you get it less times wrong with practice (I remember a time when three consecutive hards were easier than the mediums, can happen unfortunately)
And yes, that formula playing was insane. He deserves his IMO gold medal...
"This explanation doesn't actually fit with Arterm's solution, " — you're right here, I explained kinda something else :P. That resulted from the fact that I thought about problem in a bit different way which also led me to conclusion that I should count k(k - 1)...(k - m + 1) (however I didn't use it in my solution :P). However motivation behind Arterm's solution is also fine — "km counts m-tuples with repetitions, k(k - 1)...(k - m + 1) counts m-tuples without repetitions, which could be easier".
"something similar to what cgy4ever gave (...) is the only solution posted so far that doesn't use prior knowledge about Stirling numbers" — I have solved it (after contest) without any knowledge about Stirling numbers in a similar way to jiry_2. I just computed what turns out to be |s(n + 1, k + 1)| in a different manner using some DP. I posted it in a separate post: http://codeforces.me/blog/entry/44036?#comment-286886
"I agree with your conclusion -- it's a cool trick, but the fact that this solution isn't easy to come up with and that everyone else was using the Stirling formula solution makes it a bad fit for the contest format. Ideally, there shouldn't be problems for which uncommon/out-of-scope prior knowledge makes them significantly easier." — I guess you're looking at it in wrong way. Performing well in specifically TopCoder SRM 686 isn't an ultimate objective of your life. Think about it as an opportunity to learn a new interesting trick. Be thankful to Arterm that he presented interesting problem, so that you can learn more, and not 100th problem on interval trees or sth. What you're doing is like beginner whining about problem on interval trees cause he didn't know them, but just on a higher level ;p. As you can see there are various solutions to that problem and I wouldn't call it neither mechanical nor boring.
Well, you have to remember most of what I wrote was complaining about the fact that the "expected solution" used Stirling numbers. So the complaints about it being mechanical assumed that it was actually the solution contestants were expected to produce.
P.S: I still find the topic boring anyway :P But hey, if Xellos can ask for more interval trees, you can ask for more enumerative combinatorics.
Well, in fact I solved it without these crazy math. Note that tasks in TC can always be solved without advanced math / knowledge or searching online (sometimes Div1-Hard can require something a bit advance, but for Div1-Medium it will never happen).
So we want to find expectation of what returned by this code:
We can keep values of E[x0], E[x1], E[x2] .. E[xm] while running this program.
Since (x + 1)3 - x3 = 3x2 + 3x + 1, we should compile "x ++" into instructions like this:
E[x3] += 3E[x2] + 3E[x] + 1
It is not good since we need O(m2) operation for "x ++". One nature way is to replace E[x0], E[x1], E[x2] .. with other polynomials (and the degrees are still 1, 2, 3, .. m.). For example, we can amend E[x2] by adding k * E[x], when k = -1 we can find: when "x ++", we should do:
E[x2 - x] += 2E[x]
And we can replace E[x3] with E[x3 + ax2 + bx + c] such that when "x ++", we should do E[x3 + ax2 + bx + c] += k * E[x2 - x].
Then if you want to solve it by hand, you will find it is x(x - 1)(x - 2) and so on. Or you can just solve these coefficients by program.
When we want to restore E[xk] from these new polynomials, we need some coefficients. Again, you can solve it by hand and find they are Stirling numbers of the second kind, or just invert a matrix in O(m3) by program.
What is the motivation behind the polynomial transform. Does it only work with binomial coefficients or would it work with arbitrary recurrences?
Yes.
If x[i] only depends on x[j] where j <= i, then that is easy — we can do what I did above like doing Gauss elimination.
Otherwise, we can do that in theory, but much more complicated: just do diagonalization to that recurrence matrix. In case you can't get a diagonal matrix, you will get some Jordan blocks, but still we can get a matrix that has O(n) non-zero entries.
I really liked those problems, especially medium one! Judging from your problems on TC it looks like we have a very similar taste in problems ~(˘▾˘~) ʕ•ᴥ•ʔ.
div1-hard: "Could you prove it works?"
Well, no, I can't :)) it seems a really nice idea and I like a lot the problem itself. Unfortunately, I find myself unable to prove the above algo. Can you please, give me some hints that I can use to prove it?
Hi Arterm, I was looking at this editorial due to the similarity of https://codeforces.me/contest/1168/problem/E and XorPuzzle.
It seems like a key component that makes the algorithm work is that given a fixed $$$i$$$, the inner loop never repeats the same value of $$$u$$$. Can you explain why this is the case?
I find my approach to Div1Easy as pretty neat, backtrack with memoization which runs in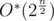 http://ideone.com/5Nlctr
http://ideone.com/5Nlctr
It's
that makes it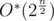 , not O * (2n).
, not O * (2n). .
.
"acc" keeps word of nonclosed brackets and it can't be longer than
Can someone help say what is wrong with my attempt at the Div1Easy? It passes all small examples I try by hand, but for the biggest example it gives a WA of 3520.
Code is http://ideone.com/m79V8Y
I know there are better solutions but this is what I came up with: DP on position, number of open round left parens (Lr), number of open square left parens (Ls), and which is the most recent open sequence (0=round and 1=square).
Thanks!
How do you keep track of the most recent open type of brackets assuming that you just closed one ?
For example..
Assume you are in a state where Lr is 5, and Ls is 5...you just closed a ')' ( it had correct turn), how do you update the most recent open sequence ? In this state you cannot know what were the order of openings of Ls and Lr.
Order matters so you need to keep track of all previous opened brackets in order, which is not doable given the constraints, I thought of your same recurrence during contest, but this was my problem , I think it might be the reason you get a WA.
I believe I handle that. The parameter "last" indicates if the current sequence of open parens is left (last = 0) or right (last = 1) or none is open (last = 2).
In your example if Lr=5 and Ls=5 then closing with ')' is only allowed if last != '['. Then continue with Lr=4.
But if Lr=1 and Ls=5, say, then closing with ')' means Lr becomes 0, which means the currently open sequence is '[' so I change "last" in the recursion. That's the point of "f(p+1, Lr-1, Ls, Lr-1?0:1)", if Lr-1 becomes 0, then the "last paren type" flips to ']'.
Hope I answered your question. Thanks.
I think that does not work...
Look at the following sequence
( [ ( [ ( [ ( [ ( [...Here you have Lr = 5, Ls = 5, and the turn is looking for ']', right ?
Explain how in your DP this state is different from
( ( ( ( ( [ [ [ [ [
Here Ls = 5, Lr = 5,and turn = ']'
However in the first one, once you close ']', your next turn should be ')', while in the second one it should be ']'. See what I mean ?
You cannot only update turn when either one goes to zero.
Hope I understood you correctly, and that I'm not wasting your time.
Wow, what a great example, you are correct, in both above cases I will continue to expect ']' whereas in the first case it should look for ')'.
THANKS!
I solved div1. 600 in fairly different way.(I didn't know Stirling numbers before....).
Suppose for a permutation P, we have n circle, and we would like to calculate n^m. We can write down as (c1 + c2 + c3 + .. + cn)^m. We can expand it as n^m tuples (c1', c2', c3', ... cm'). Here ci' can be c1 ~ cn. For a fixed m, final answer is number of different tuples (c1', c2', ... cm'), with one restriction: ci' == cj' or no common element between ci' and cj'. We can see that we only need to consider no more than 300 circles.
We can first calculate DP[N][M] using DP, number of permutations for 1 — N, which has M circles. (Which is actually Stirling number in first kind...). Then We can write final solution F(N, M) as:
Here H[a][M] means: number of distinct m-tuples using 1 ~ a, and each number appears at least one time, which can be calculated using inclusion-exclusion principle.
By simplify above format, it changed to:
We can maintain for needed N. Total complexity is O(NM + M^3).
for needed N. Total complexity is O(NM + M^3).
AC Code: http://ideone.com/cqBGdF
Nice! So, from the fact that this must be the same summation everyone else was getting, we have that
Any combinatorial proofs for this?
My solution has a large intersection with jiry_2's one, however at the time of writing that post I still don't know what this |s(n + 1, k + 1)| stands for, I used dp to count that (so no prior knowledge about Stirling numbers was neeeded).
If by dp[n][m] we denote numbers of pairs (permutation P on n elements, m cycles within P) then we get formula
(just take a cycle that 1 belongs to and let its length be k), so if we denote $D[n][m] = \frac{dp[n][m]}{n!}$ then we get
which can be easily computed. My code is here: http://ideone.com/M6ampK $O(nm + m^2)$.
And I have also computed those coefficients which turn out to be S(n, k)k! in a more direct way (it's split array) (so again no Stirling numbers :P).
Can someone explain the meet-in-the-middle approach for Div-1 Easy?