652A - Габриел и гусеница
Задача предложена пользователем unprost.
Рассмотрим три случая.
h1 + 8a ≥ h2 — в этом случае Гусеница заберётся на яблоко тот же день, поэтому ответ равен 0.
Первое условие не выполнено и a ≤ b — в этом случае гусеница никогда не сможет забраться на яблоко, поскольку она это не сделает в первый день, а после каждой ночи она будет оказываться ниже начала прошлого дня.
Если первые два условия не выполнены, легко видеть, что ответ равен
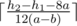 .
.
Также эту задачу можно было сдать простым моделированием, поскольку высоты и скорости были небольшими.
Сложность: O(1).
652B - z-сортировка
Задача предложена пользователем Smaug.
Легко видеть, что для любого массива можно осуществить z-сортировку. Пусть в массиве всего 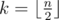 чётных позиций. Тогда можно на этих позициях расставить наибольшие k элементов массива. Очевидно после этого массив окажется z-отсортированным.
чётных позиций. Тогда можно на этих позициях расставить наибольшие k элементов массива. Очевидно после этого массив окажется z-отсортированным.
Сложность: O(nlogn).
652C - Враждебные пары
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Предподсчитаем сначала для каждого числа x его позицию posx в перестановке. Это легко сделать за линейное время. Теперь рассмотрим некоторую враждебную пару (a, b) (можно считать, что posa < posb). Запомним для каждого числа a самую левую позицию posb такую, что (a, b) образуют враждебную пару. Обозначим эту величину za. Теперь будем идти по перестановке справа налево и поддерживать позицию rg наибольшего корректного интервала с левым концом в текущей позиции перестановки lf. Значение rg пересчитывается следующим образом: rg = min(rg, z[lf]). Соответсвенно к ответу на каждой итерации нужно прибавлять величину rg - lf + 1.
Сложность: O(n + m).
652D - Вложенные отрезки
Задачу предложил Алексей Дергунов dalex.
Эта задача является стандартной двумерной задачей, которая решается с помощью одномерной структуры данных. Абсолютно аналогично решаются многие другие задачи (например, поиск наибольшей по весу цепочки точек на плоскости такой, что у каждой следующей точки обе координаты больше, чем у предыдущей). Запишем задачу формально для всех i нам нужно посчитать, количество индексов j, что выполнены следующие условия: ai < aj и bj < aj. Отсортируем все отрезки по левому концу справа налево. И в некоторой структуре данных (удобнее всего здесь использовать дерево Фенвика) будем поддерживать правые концы уже обработанных отрезков (с большим левым концом, чем у текущего отрезка). Тогда для текущего отрезка ответом является сумма на префиксе его правого конца.
Таким образом, от одной размерности задачи (от условия ai < aj) мы избавились с помощью сортировки и обработки отрезков справа налево. А от второй размерности (условия bj < aj) мы избавились использованием структуры данных (взятием суммы на префиксе).
Сложность: O(nlogn).
652E - В погоне за артефактами
Задачу предложил Алексей Дергунов dalex.
Компонентой рёберной двусвязности в неориентированном графе называется наибольшее по включению множество вершин такой, что между любой парой вершин существует два рёберно-неперескающихся пути. Рассмотрим граф в котором вершинами являются компоненты рёберной двусвязности исходного графа. Легко видеть, что этот граф является деревом (если бы в нём был цикл, то компоненты цикла образовывали бы одну компоненту двусвязности). Поскольку рёбра исходного графа разрушаются после прохождения по ним, мы не можем перейдя по ребру этого дерева вернуться назад (поскольку это дерево).
Рассмотрим компоненты двусвязности в которые попали вершины a и b. Обозначим их A и B. Утверждение: ответ YES если и только, если на пути в дереве между вершинами A и B либо есть ребро дерева с артефактом, либо есть компонента содержащая внутри себя ребро с артефактом. Легко видеть, что утверждение верно: если такое ребро есть, то мы либо пройдём по нему пока будем идти по дереву из A в B, либо можем пройти по нему внутри компоненты (ведь внутри компоненты между каждой парой вершин есть два рёберно-непересекающихся пути). Обратное также легко непосредственно проверить.
Одним из способов выделить компоненты рёберной двусвязнсти является следующий:
Ориентируем исходный неориентированный граф по обходу в глубину (для каждого ребра запомним в каком направлении мы впервые захотели пройти по нему).
Выделим в этом ориентированном графе компоненты сильной связности.
Утверждение: компоненты сильной связности нового графа будут совпадать с компоненты рёберной двусвязности исходного графа.
Также в этой задаче можно было заметить, что рёбрами дерева будут мосты (мосты в смысле теории графов, а не легенды из условия). Поэтому для решения задачи достаточно выделить мосты в графе.
Сложность: O(n + m).
652F - Муравьи на круге
Задача предложена пользователем Lewin Gan Lewin.
Наблюдение 1: если для нас муравьи неразличимы, можно считать, что никаких столкновений не происходит, а муравьи просто проходят друг через друга. Таким образом, мы можем легко узнать положения всех муравьёв в конце, но мы не можем сказать какой муравей где находится.
Наблюдение 2: относительный порядок муравьёв никогда не меняется.
Таким образом для решения задачи нам достаточно определить положения хотя бы одного муравья по прошествии t единиц времени.
Будем решать эту задачу следующим образом:
Рассмотрим положения муравьёв по прошествии m единиц времени. Легко видеть согласно первого наблюдения, что положения муравьёв остнутся исходными, но порядок изменится (произойдёт циклический сдвиг порядка). Найдём этот циклический сдвиг sh и применим его
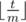 раз.
раз.После этого останется
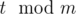 единиц времени.
единиц времени.
Таким образом, задача свелась к тому, чтобы промоделировать процесс для одного муравья за время m и за время 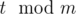 . Заметим, что за промежуток времени не больший m один фиксированный муравей не может столкнуться с другим муравьём более двух раз. Таким образом, если мы будем игнорировать столкновения всех остальных муравьёв кроме фиксированного всего произойдёт не более 2n столкновений.
. Заметим, что за промежуток времени не больший m один фиксированный муравей не может столкнуться с другим муравьём более двух раз. Таким образом, если мы будем игнорировать столкновения всех остальных муравьёв кроме фиксированного всего произойдёт не более 2n столкновений.
Давайте моделировать этот процесс с помощью двух очередей муравьёв идущих влево и вправо. Каждый раз мы должны брать в очереди противоположного направления первого муравья, обрабатывать столкновение и кидать его в конец очереди другого направления.
Подсказка: если у вас возникнут проблемы со случаем, когда муравей может попасть в две позиции, просто промоделируйте процес со следующим муравьём.
Сложность: O(nlogn).











Hello,
A) Thx for contest .. I loved the problem-set :)
B) I see one of the complexities in Russian in English version [problem 'D'] : "Сложность"
Hi Edvard
About C In such a situation: arr: [2, 4, 3, 1] Foe = (2,1), (3,4)
z[0]: {3}z[1]: {2}Your solution will work like this :
Initially, ans = 0, rg = 3ans += 3 , (i=0, rg = 3)ans += 1 , (i=1, rg = 2)ans += 0 , (i=2, rg = 2)ans +=-1 , (i=3, rg = 2)So your answer is = 3
but clearly the answer is 6
In arr: ((2,2), (4,4), (3,3), (1,1), (2,4), (3,1))
In index: ((2,2), (4,4), (3,3), (1,1), (0,1), (2,3))
Please tell me if I am missing something.
I think that's because author is using very many redefinitions.
Please check the code of the solution. The solution will be more clear for you after that.
Hi Edvard
I am quoting the code in the solution. As per the code you shared the solution for this example is 3: arr: [2, 4, 3, 1] Foe = (2,1), (3,4)
But there are 6 intervals. So either the code is not correct or I am missing something. Please do have a look.
Thanks
In the outer for-loop ,loop variable 'i' is decreasing (from n to 1 ,written as 'nfor' ).
Solution to problem E please!
For the time being, W4ynebot wrote a solution in the announcement blog, you can read it.
Hello everyone . Can someone please Help me in solving Problem A? I have seen several Solution . But failed to understand .
Can Anyone please Help ??
Let's say we have this input data:
This means that at 2 PM there is an apple on the tree at height of 90 cm, and at 10 cm height sits the caterpillar. We know, that between 10 AM and 10 PM caterpillar goes higher 4 cm/hour. When it's 10 PM caterpillar goes to sleep and slips down 1 cm/hour, until it's 10 AM again. So we have the process:
In our case caterpillars movements are:
In the middle of the 2-nd day the caterpillar is high enough to reach the apple, so the answer is 2.
"sleeping" ?? :D Sorry for nitpicking. You clearly meant "slipping".
He slips while sleeps :D
Oh yeah, you mentioned! I surely ruined the fun out of it! ;) By the way, were you the author of this problem? (I can't find the author information for any particular problem! :| )
I've suggested this problem and Edvard prepared it
And who invented the story?
I'm sure you can guess :D
Genius Simply .. I like the Statement & Way of your Derivation .
I thought that since the boy's school is closed at 2 pm, so he sees the caterpillar first at height h1 at 2 pm . So, the caterpillar should be at 10 cm height at 2 pm . I think a little more careful problem statement was required in A .
Any thoughts on problem F?
You need to make a couple of observations:
The final complexity is .
.
Hopefully that made some sense, it should be enough to solve the problem. Here's my solution by the way: 16961705
EDIT: Here's an even shorter solution: 16970841. Very simple compared to the one in the editorial :)
Actually it can be solved without any simulation. Time still will be O(n ln n) due to sort.
Very nice! It looks that W4yneb0t implemented that solution.
I had troubles understanding this. Could you give a more detailed proof on why this works please?
Which part needs explanation?
I don't understand why this would work. How come ((S*T)mod(N*M)-O)/M = answer.
See some formulas below.
Can you explain why "p_1 is equal to q_(1+offset)" ?
It's not equal, it means that ant from position p1 will move to position q1 + offset. Here is a proof:
Let ant from position p1 finishes at position q1 + t. Then ant from p2 moves to q2 + t etc. Then total (oriented) movement (total oriented distance traveled by ants) equals
(last t summands have +m because ant will go full circle before arriving to that position). On the other hand it equals S·t. So t = (St - O) / m.
I don't really understand this idea, could you explain why you add m. Isn't everything already mod m, why would it matter?
Edit: actually I am more confused now why the left hand side is equivalent to S*t.
Positions are mod m in a sense, but e.g. speeds aren't.
Left side is S*t because it's total oriented movement. So on the one hand it's speed multiplied by time, on the other — difference between finish and start positions.
But the offset doesn't seem like enough, for example a single ant can go around the circle many more than 1 time but this doesn't seem to be accounted for in the total oriented movement.
Another solution without simulation:
First, relabel the ants such that they are in increasing position with respect to their indices. We can reverse this relabelling at the end.
Next, imagine that each ant has a sign. When two ants pass each other they exchange signs. Consider the first ant (assume he is going right) — we know where it will eventually end up but we do not know what sign it will hold. Notice however that when the first ant meets another ant, the sign the first ant holds will increase by one. So we simply sum up how many times the first ant meets another ant.
Nsqrt(N) giving TLE in problem D :(
Nsqrt(N) = 1e9 for max test.
no N = 2e5 so NsqrtN ~ 1e8
yeah my bad
this is my solution to problem D 16932540
it get TLE, i don't use BIT but use erase function n times, how much erase function cost???
erase works in O(log n), however, the following code runs in O(n):
int k = lower_bound(vv.begin(), vv.end(), v[i].first.second)-vv.begin();
thus complexity of your solution is O(n^2)
Hello,
I got question!
here I made two submitions of problem "D"
Accepted and TLE
The only difference in between them is "map" and "unordered_map" (One of them got TLE second Accepted (TLE with unordered_map))
it was hacked by this generator:
Anyway when I executed it in locale, the unordered_map is faster.
Can somebody please explain the magic behind this? :) Thx
I was also hacked by this generator, but solution with unordered_map took ~7s and solution with map took ~0.38s on my machine.
Hmm interesting ... I have "0m0.370s" for hash map and "0m0.583s" for map :/
interesting :)
Did you decrease the maximum load factor of the unordered_map when testing on your machine? Doing so makes the code faster and even acceptable.
I'm sorry, I'm afraid I don't understand, what "load factor" means
I just generated exact input and run it with "g++ -Wall -pedantic -Wno-long-long -std=c++11" (with the codes from above :/ )
You can check it out here. Since you didn't do it, it's pretty interesting that the solution with unordered_map ran faster on your machine.
Oh, didn't know about this ~ Thx! :)
Visual Studio STL is different from GCC STL (aka libstdc++). For example, the following code
prints 100001 for GNU G++/GNU G++11 and 1680716807 for Microsoft Visual C++ 2010. Also, unordered_set and unordered_map implementations themselves are probably different. So different STLs require different anti-hash tests. I guess that you are testing your program with Visual Studio while my anti-hash test is designed for gcc STL.
Nope, I tested under GCC STL (I think 4.7 version — if it can influence anything?)
anyway interesting (nice hack btw — didn't even know about the possibility ^_^ )
std::cout << std::hash()(N) << std::endl; returns same numbers as are arguments :O is it right?
Thx man and have nice day!!
Well, if my test doesn't cause slowdown, gcc version must influence something. There are nothing else to blame.
Yes (for gcc STL).
It's also possible to solve the problem B in O(n).
Code: 16934709
I believe this exact same problem exists in codechef's ex Easy section! And I did it the same way!
Can we use MO's Algorithm for solving D ?
complexity seems good. but I tried it and I got TimeLimit
I don't know why ? can anyone help me. tanx
I use too and I got TLE ;/
http://www.codeforces.com/contest/652/submission/17020791 using Mo's
thanks! :)
Here's my solution to Problem E: 16955949
As explained in the editorial, we are interested in all Edge-Biconnected-Components on the path from a to b. Instead of building the EBCC-tree, we can easily obtain all vertices in these EBCCs by adding a new edge between a and b. Since it was given that there is a path between every pair of vertices, there are now two paths between a and b, and hence, they are in the same EBCC. Furthermore, all EBCCs in the original EBCC-tree will be contracted to a single component.
To find this EBCC, I used our normal code to find bridges and biconnected components, together with Union-Find. For every edge that is not a bridge, I merge the two (components) of the endpoints of the edge. Afterwards, I merge the components of a and b separately, because the algorithm fails when there is only a single edge between a and b.
Next, for every edge with an artifact, I check whether both endpoints of the edge belong to the component of a and b (using the Union-Find datastructure we built earlier). If there is such an edge, the answer is 'YES'. Otherwise, print 'NO'.
All together, this solutions requires almost no code apart from reading the input, the Union-Find and Biconnected Components algorithm.
Really brilliant idea to add edge from a-b to make they are in same EBCC.
btw, if you can find EBCC correctly for multigraph, then only needed work is for any artifacts (u, v) check u.bcc == a.bcc and v.bcc == a.bcc.
Here is my code: click
In the code, used 'metParent' variable to handle multigraph(so if u — v have multiple edges, then do not classify as bridge)
Can anyone please explain C using two pointers..I have been trying for 2 days but all my efforts are in vain.....Please???????????????
In a sorted array work this rules:
So you sort the array, and then build a new one using pair of pointers
(1, n)or(1, mid)making one of this sequences:The first one is simpler to implement, considering the case where n is odd
Thanks for the quick tutorial. Can you please tag the contest to this tutorial?
Done.
I think there are typos in the explanation of problem A:
In point 2, it should be
a<=binstead ofa>b.In point 3, it should be
ceil((h2-h1-8*a)/(12*(a-b)))instead ofceil((h2-h1)/(12*(a-b))).Thanks. Fixed.
Shouldn't the complexity of C be at least O(n log n) . See these two for loops :
nfor(i, n) { forn(j, sz(z[i])) rg = min(rg, z[i][j]); ans += rg - i; }Can anyone please explain a little bit ?The total size of all z[i] is O(m). I've fixed the complexity from O(n) to O(n + m).
BTW, problems were really nice . Just A's problem statement was tough to understand.
How is the complexity O(n+m) ? If all the z[i]'s contains elements in decreasing order , then the second 'for' loop will have a complexity O(n) .
z[0] + z[1] + ... + z[n — 1] = m
In Problem E How to solve if changing the route which originally (a to b) to (a to b then back to a)? Thanks!
Hi, Can anyone explain the editorial for problem D? I am unable to understand the use of Fenwick Tree for this particular problem. Also I am not sure but there seem to to be some typos in the editorial i.e bj<aj instead of bj<bi in fourth line and bj < bj instead of bj<bi in second last line. Please correct me if I am wrong?
Good day to you,
let's say you have an array (later Fenwinck → complexity) and for every END of segment, you add 1 to the value (I mean => if you have segment [1,5], then you do Array[5]++)
PS: A necessary here is to make the values lesser (but preserve their order). So from [1,10000000],[3,50000], you would do [1,4][2,3] (otherwise you would not have enough memory for it)
Now let us sort the array of segments by their beginning.
Here, for every segment you do following operation:
I) Sum all values of all elements of array, from 0 to END
II) Substract END of this segment from array (so for [1,5] you would do Array[5]--)
Now see, what happened to all segments. The sum of values is the number of ends, which end earlier, than END of current segment. How can we be sure that we didn't include any extra segment? Well it is thanks to (II). Here we already substracted values of ALL segments, which begin earlier, then our current segment (so we are considering only points which begin later and we are searching for those, whose END is earlier, than current END).
Here you see, that the complexity is O(N^2). It is time to use Fenwick. It has exact property we want! Add/Substract a value of any one element (in logarithmic time) + get the sum of 0→END also in logarithmic time!
If the explanation was confusing, or not enough, do not hesitate and ask for additional questions :)
Good Luck man! ^_^
Thanks man. I got the idea.
How to know when to use Fenwick tree ?
I have an alternate solution to F (maybe it's already in the editorial if I didn't read it properly).
Like in the editorial, we reduce the problem to finding the location of a single ant after x time units.
We plot the lines for each of the ants on the Cartesian plane, and "repeat" them with period m so that we have all the necessary lines. By necessary, I don't mean all infinity lines, because we only care about and will only query for up to m time units. This means that for the second sample input:
The lines for the ant
5 Larey=-x-3,y=-x+5andy=-x+13. All other lines are irrelevant, because we can never reach them.Now, notice that for any ant, it follows a path on the lines, and each time it reaches an intersection, it swaps — it jumps to another line. We can observe that this means that if the ant starts at the k-th lowest line, it always stays on the k-th lowest line.
So since we have all necessary lines, we can find the value of k, and then find the k-th lowest y-coordinate to find the final location of the ant.
We can use this algorithm to find the cyclic shift per period, as well as the final movement of the ant.
Accepted solution: 17126112
I am trying to understand the complexity of the below submission for problem E (Its a nicely written code, btw).
http://codeforces.me/contest/652/submission/16927126
Especially the below line in
dfsThe
findmethod takesO(N). How to prove that the overall solution will not haveO(N^2)for some worst case scenario?Hi! I wanted to share my solution for the problem D, using order statistics tree (see this article for more info about the data structure): My solution
dalex could not understand your solution for problem D. Please explain.
Try this:
My solution is available in my last submits.
Задачу Д можно решать с помощью данной структуры: http://codeforces.me/blog/entry/11080 Решение: http://codeforces.me/contest/652/submission/27927876
For problem E Pursuit for Artifacts, is it always possible to have a path from A to B passing some artifact edge E if all of them are in same biconnected component?
It's true, but it's not that easy to be proved. Every biconnected graph can be constructed as follows: first we have a loop, and each time we add a path on it. We choose a loop that contains an artifact edge E, then we can construct a path passing the edge E, by moving vertex A and vertex B to older paths or loop in the structure above.
Yes. Let (u,v) be the artifact edge. Suppose for every path p1 from A to u and p2 from B to v inside the component p1 and p2 have common edges. You can see that there exists a certain edge e* in the component for which every such pair of paths p1' and p2' pass through, otherwise you can construct disjoint paths. This edge e* separates the biconnected component in two which leads to a contradiction.
In problem E, what is the proof that if a single bi-connected component (let's call it $$$A$$$) has a 1-edge, then you one can go from any point in $$$A$$$ to any other point in $$$A$$$ that travels this 1-edge and never visits the same edge twice?