628A - Теннисный турнир
Задача предложена пользователем unprost.
В этой задаче можно было просто промоделировать процесс. А можно было заметить, что после каждого матча один игрок выбывает. Всего выбывших n - 1. Таким образом, всего нам нужно (n - 1) * (2b + 1) бутылок воды. Полотенец, конечно, нам нужно np штук.
Сложность: O(log2n), O(logn) или O(1) в зависимости от реализации.
628B - Новый скейтборд
Эта одна из задач предложенных пользователями Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
Ключевым для решения задачи является наблюдение, что число делится на 4 тогда и только тогда, когда его последние две цифры делятся на 4. Таким образом, для подсчёта ответа достаточно сначала посчитать количество подстрок длины один. Далее нужно рассмотреть пары соседних цифр таких, что они образуют двузначное число кратное 4-м и прибавить к ответу индекс правого из них.
Сложность: O(n).
628C - Медведь и расстояние между строками
Задачи предложена и подготовлена Камилем Дебовски Errichto.
В этой задаче можно действовать жадно. Будем идти по строке слева направо. Рассмотрим наибольшее расстояние d, которое мы можем получить на этой позиции (это либо расстояние вниз до буквы 'a', либо вверх до буквы 'z'). Пусть v = min(d, k). Поставим на текущей позиции букву на расстоянии v (вниз или вверх), а значение k уменьшим на v. Если после обработки всей строки, k оказалось больше нуля, то ответа не существует. В противном случае мы нашли ответ.
Сложность: O(n).
628D - Волшебные числа
Более простую версию задачи предложил Kareem Mohamed Kareem_Mohamed.
Обозначим ответ на задачу как f(a, b). Заметим, что f(a, b) = f(0, b) - f(0, a - 1) или что то же самое f(a, b) = f(0, b) - f(0, a) + g(a), где g(a) равно единице если a является волшебным число, иначе g(a) равно нулю. Далее будем решать задачу для отрезка [0, n].
Далее приводится стандартная техника, которую иногда называют 'динамикой по цифрам'. Её можно реализовать двумя способами, в первом перебирается длина префикса числа, который совпадёт с префиксом числа n. Следующий символ может быть произвольным меньшим соответствующей цифры в n, а далее любые цифры. Но я расскажу о втором подходе.
Пусть zijk равно количеству волшебных префиксов длины i, дающих остаток j при делении на m. При этом если k = 0, то префикс должен быть строго меньше префикса числа n, а если k = 1, то префикс должен быть равен префиксу числа n (больше он быть не может). Будем делать динамику вперёд. Переберём цифру 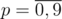 , которую мы поставим на позиции i. При этом нам нужно проверить, что если позиция чётна то эта цифра должна быть равна d, а в противном случае она не может быть равна d. Также нужно проверить, что если k = 1, то эта цифра не может быть больше соответствующей цифры в числе n. Теперь поймём в какое состояние мы попадём после такого перехода. Конечно, i' = i + 1. Согласно схеме Горнера j' = (10j + p) mod m. Легко видеть, что
, которую мы поставим на позиции i. При этом нам нужно проверить, что если позиция чётна то эта цифра должна быть равна d, а в противном случае она не может быть равна d. Также нужно проверить, что если k = 1, то эта цифра не может быть больше соответствующей цифры в числе n. Теперь поймём в какое состояние мы попадём после такого перехода. Конечно, i' = i + 1. Согласно схеме Горнера j' = (10j + p) mod m. Легко видеть, что 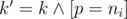 . Для перехода нужно сделать zi'j'k' + = zijk. Конечно, нужно не забыть делать все операции по модулю 109 + 7.
. Для перехода нужно сделать zi'j'k' + = zijk. Конечно, нужно не забыть делать все операции по модулю 109 + 7.
Сложность: O(nm).
628E - Zbazi в Zeydabad
Задача предложена Ali Ahmadi Kuzey.
Давайте сначала сделаем предподсчёт zlij, zrij, zldij — наибольшее количество букв 'z' влево, вправо и влево-вниз от позиции (i, j). Это легко сделать за O(nm). Пусть мы зафиксировали некоторую клетку (i, j). Рассмотрим величину c = min(zlij, zldij). Это наибольший допустимый размер квадрата с верхним правым углом в (i, j). Теперь поймём сколько таких квадратов. Рассмотрим произвольную клетку (x, y) по диагонали вниз-влево на расстоянии не более c. Пара клеток (i, j) и (x, y) образует z-паттерн, если y + zrxy > j.
Отлично, теперь для решения задачи заведём структуру данных для каждой диагонали (она определяется формулой x + y), которая умеет прибавлять в точке и брать сумму на отрезке (лучше всего для этого подходит дерево Фенвика). Будем перебирать столбец j справа налево и обрабатывать события: некоторая клетка (x, y) такова, что y + zrxy - 1 = j. В этом случае нам нужно в дереве номер x + y сделать прибавление в точке y на единицу. Теперь будем перебирать клетку в текущем столбце (i, j). Тогда к ответу нужно прибавить величину суммы в дереве номер i + j на отрезке от j - c + 1 до j.
Сложность: O(nmlogm).
628F - Медведь и справедливое множество
Задача предложена и подготовлена Камилем Дебовски Errichto.
Вначале для удобства добавим подсказку с upTo = b, quantity = n, а затем отсортируем подсказки по значению upTo. Отсортированные подсказки разбивают интервал [1, b] на q непересекающихся промежутка. Для каждого промежутка мы знаем количество элементов в нём.
Для решения задачи построим сеть (описанную ниже) и найдём в ней максимальный поток. Ответ fair только если величина потока равна n.
- Первая группа вершин в сети A будет содержать 5 вершин, обозначающих возмоджные остатки.
- Вторая группа вершин B будет содержать q вершин, обозначающих промежутки.
Соединим каждую вершину из A с истоком ребром пропускной способности  . Каждую вершину из B соединим со стоком ребром пропускной способности равной количеству чисел в этом промежутке. Между всему вершинами x из A и y из B добавим ребро пропускной способности равной количеству чисел в промежутке с остатком x в промежутке y.
. Каждую вершину из B соединим со стоком ребром пропускной способности равной количеству чисел в этом промежутке. Между всему вершинами x из A и y из B добавим ребро пропускной способности равной количеству чисел в промежутке с остатком x в промежутке y.
Легко видеть, что поток в данной сети очень похож на паросочетание. В самом деле мы можем воспользоваться теоремой Холла. Для каждого из 25 множеств вершин из A (множества остатков) пройдём по всем промежуткам и посчитаем количество чисел, которые мы можем взять в [1, b] с остатками в заданном множестве.
Реализицая с теоремой Холла: C++ solution.
Сложность: O(2Cn), где в нашей задаче C = 5.











Thank you for fast editorial.
Extra challenge for 628C - Bear and String Distance — can you find the lexicographically smallest answer?
Try to replace all character with smaller ones. If k > 0 in the end, start from the end, and if bigger si makes k smaller, we will replace it and so on. If k equals 0, answer is this, else answer is - 1.
Congratulations! It's correct if by "smaller ones" you mean letter 'a'.
So problem F wasn't about flows. Can anyone hack flow solutions? I'm not sure if it's possible because the graph is special.
I'm also waiting for the hacks against flows.
It seems that it is impossible to hack even naive flows. Burunduk1 suggested two tests where flow solutions works in O(b2) time (and he says that it's a maximum time we can get here), but it's not enough. If we set the constraints b ≤ 2·105 then it'll be possible to hack flow solutions.
Why n was so small in F? I spent a lot of time trying to find alternative solution because this time complexity looked too good to be true. Luckily, I was able to prove the algorithm, shrugged and got OK 5 minutes before the end of the contest.
We was discussed for a long time with Errichto the constraints. And finally we decided to make it smaller because with small C it's harder to come up with solution.
I don't get it. You tried to make problem harder by reducing n (and making the best solution looking too fast) or easier by allowing flow solutions?
PS. It was quite unexpected to end up in the first place. I should thank participants who hacked everyone above me.
On my mind with constraint C = 5 it's harder to come up with solution. The small constraints for the n, b are our fault, we should make it 5·105 and then we could hack all flow solutions (except maybe Dinic solutions). P.S.: Congrats with the first win!
in ques E what does this do?
for ( ; i < m; i |= i + 1) t[i] += v;
https://en.wikipedia.org/wiki/Fenwick_tree
what kind of bit is this ? can you explain the bit ? this is the sum function : for ( ; i >= 0; i = (i & (i + 1)) — 1) ans += t[i];
noone know how it works. it's just magic)
The key thing here is the
+ 1part. Why do we need adding1at all?Well, let's look at the binary representation of some number
x = ...01111.Now, let's add
1to the numberxand see howx + 1looks like:...01111 + 1 =...10000The
x + 1has lost all it's ones at it's end!Whatever the
xnumber is, we know that it has exactly 4 consecutive ones at it's end. If we add1to that number, the last group of 4 consecutive ones will change to zeros.If the number
xhas0as it's last digit, the change after adding1will be not as dramatic :)...01110 + 1 =...01111Notice, that in this case
xandx + 1differ only in a single digit.For problem B, I saw some solutions whereby people constructed the 2 digit numbers by the following way: num = str[i]*10+str[i+1]
Although, it should have been: num = ( str[i] — 48 ) * 10 + ( str[i+1] — 48 )
I have no idea as to why is the former still working (passing the pretests) ?
Because 48 % 4 == 0 (coincidence)
in D why the answer for this test 43 3 587 850
is 1 ????? what is the number which is multiple of 43 and 3-magic??? where am I wrong???
731
oooh, thanks, I mis-write the number on the calculator. I thought I misunderstood the problem.
In problem D, how is next next dp state calculated? I'm not able to get it. Also why are we having k = {0, 1} as third dimension in our dp. Why was there a need to introduce it in the dp?
In Problem D, How to solve f(0, a)? It may contain leading zero when len(i) < len(a). I know in the problem len(a) == len(b), so we don't care about such case. But I just wonder how to calculate the value of f(0, a).
In E, is y-axis directed down-to-up? Otherwise y + zrxy > j will always hold..
Also, do I understand correctly, that we can't "precompute" the whole Fenwick tree (for each diagonal of course) and only then make the queries? Otherwise we could go with simple prefix sums. I think this "dynamicness" makes it harder to come up with the solution.
Finally got it. The keyword for me was "events", I didn't pay attention to it while reading the solution. Though I still don't understand the order in which the editorial's solution processes the map.
In problem F, when we are finding matching, what is mapped against what? What do you mean by 2^5 vertices?
There are 5 vertices in the first group so there are 25 sets of vertices.
I don't understand your question "what is mapped against what?", so I will just write a bit about the matching thing. We have a bipartite graph with two groups of vertices, described in the editorial. It's a problem similar to matching (or vertex cover) problem but for each vertex we have some required degree (the number of incident edges in "matching"). E.g. each of 5 vertices in the first group should be incident to n / 5 edges chosen in matching. You can think that such a fake vertex represents n / 5 real (true) vertices, all connected to the same vertices from the second group. The same applies to the second group — e.g. the interval where we want the degree 3 represents 3 real vertices. After replacing fake vertices described in the editorial with real vertices you would get a bipartite graph with exactly n vertices in each of two groups. And then we ask about the perfect matching.
Is this some other kind of hall marriage theorem? The one I knew was applying only for bipartite graphs. Indeed, you could convert some nodes as you said, but the huge problem is that we have edges between the two groups with capacities more than 1. Could you explain more thoroughly how to bring the problem to the form of a bipartite graph, maybe with some example? If we replace an interval with q nodes where q is the number of numbers we know Limak will have in that interval, then, from those nodes, exactly what edges will you draw? If you want to draw the same edges as before replacing the intervals, then you'll need capacities and it's just not right...Could you actually give an example? I find it strange that in your source you checked for something to be in an interval. The hall's theorem that I know only requires for an inequality (not two as in your case) to hold. Firstly, I really don't believe that there is any way to change the network in one with capacities of 0 or 1. Secondly, even if we did, as long as the obtained network is not bipartite (maybe tripartite?), I wouldn't know how to apply the theorem. Sorry for the question, but I already spent an hour trying to understand and didn't succeed. Hopefully, your answer could help others as well
I don't understand problem D.Why number 1 is 7-magic?Digit 7 doesn't appear in it at all.Maybe there is a bug with problem statement?Maybe there is no comma between 17 and 1?
Do you see any even position with some
digit != 7? I don't.Thanks.I get it now.
Edit:I originally thought 7 has to appear at least once on even position and not appear on any odd position.
So 7 has to appear on EVERY even position?For example 172738 is not 7-magic right?
Problem F:
i though the complexity of dinic is O(V^2*E) where V = number of Nodes and E= Number of Edges . Here V is maximum 10^4 . then how can Dinic solution pass for this problem ? Can someone tell me what i'm missing ?
Dinic algorithm complexity can be improved to O(V*E*log(V)). It is the improved version that everyone uses in the contests. Since E is only O(n) in this problem, the running time is only O(n^2*log(n)).
I read a bit more on flow algorithms and I am no longer sure what is time complexity of the standard algorithm. But in this problem the maximum flow is only O(n) with integer capacities and so all algorithms work pretty fast.
I know only complexity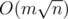 for the networks with capacities equals to 1. Complexity in general case of course O(n2m) as written above.
for the networks with capacities equals to 1. Complexity in general case of course O(n2m) as written above.
I am not able to understand the editorial of problem E.
Problem E,the last few words should be x + y? 'i' wasn't mentioned before.
For problem D, I am getting constantly TLE on test case 16. I have used top-down memorization approach. I do not understand why it's getting tle because I used maximum dp states of order 10^7. which should get run easily ? hers is my Submission
can someone tell me the reason of getting even after using dp for problem D ?
Here is my Submission
Problem E can be solved without using fenwick tree, maintaining 2 pbds is a bit easier i believe as if we move along anti diagonal from the right, our requirement of one value increases and after removing all unwanted instances of it from the 1st set and from it's second mirroring one, we just need count of all elements satisfying another value range.
Can someone please help me with the D problem. I came up with a solution similar to one in the editorial. The only difference in the implementation is that in editorial forward dynamic programming is used, whereas I calcuated in bottom-up manner. I am unable to reason out, why I am getting TLE. Here is a link to my solution : https://codeforces.me/contest/628/submission/82218592
Hi, Thanks for providing solution. I think in your solution you passed string without references so, it gets created every time function calls. try to pass it by reference, it'll reduce time and you can avoid TLE.