A. Решение в лоб за O(n) (моделирование всех n раундов) получает TL. Ускорим наивное решение — рассмотрим раунды на отрезках [1..mk], [mk+1..2mk], [2mk+1..3mk] и так далее. Нетрудно заметить, что результаты раундов на этих отрезках будут повторяться. Поэтому промоделируем только один из этих отрезков, а затем учтем его [n/(mk)] раз ([x] — деление нацело). Остаточек из n%(mk) последних раундов промоделируем отдельно. Итого получаем решение за O(mk), которое легко проходит по времени.

Авторы — Ripatti и Gerald .

B. Построим двудольный граф на n+m вершин. Вершины из первой доли соответствуют строчкам, вершины из второй — столбцам. Ребро соединяет две вершины тогда и только тогда, когда на пересечении соответствующих строки и столбца находится колонна.

Изначально луч смерти полностью покрывает только последнюю строчку таблицы — то есть, только одну вершину в нашем графе. Когда мы делаем колонну магической, то мы даем "пройти" лучу в графе по соответствующему ребру.

Теперь задачу можно переформулировать следующим образом: нужно "активизировать" наименьшее число ребер в двудольном графе так, чтобы имелся путь из вершины, соответствующей последней строчке таблицы, в вершину, соответствующей первой строчке таблицы.

Понятно, что искомое множество ребер — кратчайший путь между этими вершинами. Его можно найти с помощью поиска в ширину (BFS). Если BFS ничего не нашел — ответ -1.

Это решение работает за O((n + m)²).

Автор — haas.

C. Переберем все спирали в лоб и потом выберем ту, на которой сумма максимальна. Так как всего спиралей порядка O(n³), то пересчитывать значения для каждой из них надо за O(1) чтобы решение прошло по времени.

Будем действовать следующим образом. Зафиксируем какую нибудь клетку, после чего будем перебирать все спирали с центром в этой клетке, от самых маленьких, к самым большим. Как за O(1) делать переход показано на рисунке:

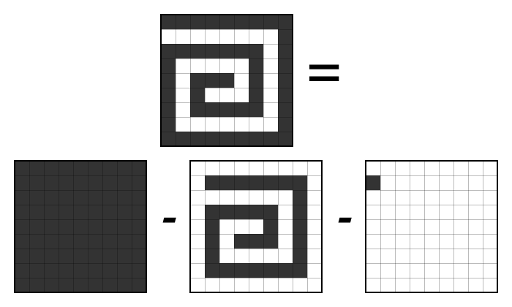
Чтобы посчитать первое "слагаемое", нужно предварительно посчитать частичные суммы на прямоугольниках.

Автор — Ripatti.

D. Итак, нам дан двудольный граф на 3k вершин, надо его раскрасить в k цветов так, чтобы каждого цвета было ровно по 3 вершины и любое ребро соединяло вершины разных цветов.

Сначала разобьем граф на доли, например, с помошью обхода в глубину. Посмотрим на размеры долей.

Случай 0. Если они оба делятся на 3, то отдельно для каждой доли разбиваем на тройки и красим.

Иначе, можно считать, что размер первой доли равен 1 по модулю 3, а второй — 2 по модулю 3.

Тут еще 2 случая, которые удобно рассмотреть последовательно:

Случай 1. Надо попытаться найти одну вершину в первой доле и 2 вершины во второй доле, попарно не связанные ребрами. Если нашли — красим их в один цвет, сводим к случаю 0.

Случай 2. В случае неудачи случая 1 надо попытаться найти 2 вершины из второй доли, каждая из которых связана "антиребрами" с двумя вершинами из первой доли (итого 4 вершины из первой доли, 2 вершины из второй). Если нашли — красим их двумя цветами и сводим к случаю 0.

По поводу реализации: не совсем понятно как разобрать случай 2 за приемлемое время. На самом деле подойдут любые две вершины второй доли, из которых исходит по два "антиребра". Эти "антиребра" не будут вести в одинаковые вершины, иначе бы мы уже получили решение в разборе случая 1.

Если ни один из случаев не дал результата — ответ NO.

Итого решение за O(n+m).

Автор — Ripatti.

E. Представим всех людей как точки на плоскости с координатами (x = a_i, y = r_i). Какое максимальное количество людей может войти в группу с фиксированным лидером (x_i, y_i)? Ответ на этот вопрос — это количество точек в области (x, y) : x_i - k ≤ x ≤ x_i + k, y ≤ y_i.

Найдем как-нибудь, для каждого человека такое количество. Теперь пусть у нас есть запрос, какая максимальная группа содержит точку (x_i, y_i) и (x_j, y_j). Раз в этой группе должен быть лидер, то его возраст должен быть в границах от max(x_i - k, x_j - k) до min(x_i + k, x_j + k), а значение ответственности  ≥ max(y_i, y_j). Среди все таких лидеров, нужно всять такого, размер максисимальной группы которого, максимален. По сути этот запрос, запрос на максимум в области похожей на область, которая была рассмотрена выше.

Опишем, как быстро отвечать за запрос количества точке в области, которая имеет специальный вид (максимум аналогично). Сожмем координаты по x. И построим дерево отрезков по сумме на них. Дальше будем рассматривать все запросы в порядке увеличения координаты y. Когда расссматриваем группу запросов с одинаковым y, делаем сначала прибавление в точки x соответсвующие запросам из группы, после этого ответ на запрос это сумма на отрезке от x_i - k до x_i + k.

Таким образом мы обработаем все запросы за n·log(n) в offline. Запросы на максимум обрабатываются аналогично.

Автор — havaliza.