Задача 168A - Волшебники и митинг Автор PavelKunyavskiy.
В этой задаче надо было написать ровно то, что было описано в условии. В частности, надо было чтобы на митинг пришло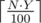 
людей. Соответственно, для этого надо было создать 
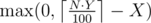клонов.
Задача 168B - Волшебники и минимальное заклинание Автор PavelKunyavskiy.
В этой задаче опять-таки надо было написать ровно то, что было описано в условии. Считываем строки по одной. Кроме того храним последний блок строк, не являющихся усиливающими. Если очередная строка — усиливающая (что проверяется линейным проходом), то выводим последний блок, если он есть, и саму строку. Иначе удаляем из строки все пробелы и добавляем к последнему блоку. Остается только различить пустой блок и блок из пустых строк.
Задача 167A - Волшебники и троллейбусы Автор Alex-Gran.
В этой задаче наконец-то надо было немного отойти от перевода условия на язык программирования. Из условия, что ускорения всех троллейбусов одинаковы, а замедляться они могут моментально, следует, что ответ для очередного троллейбуса это максимум из времени когда он приехал бы, если бы ему не мешались остальные троллейбусы и времени приезда троллейбуса, который ехал прямо перед ним. Осталось только посчитать время приезда троллейбуса. Здесь проще всего разобрать два случая. Если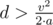 
, то троллейбус успеет разогнаться полностью и ответ будет равен 
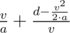. Иначе троллейбус будет разгоняться все время и ответ будет равен 
.
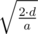Задача 167B - Волшебники и здоровенный приз Автор PavelKunyavskiy.
Эта задача решается методами динамического программирования.
Пусть d[i][j][k] — вероятность того, что из первых i дней мы выиграли j и набрали сумок суммарной вместительностью m. Для удобства будем считать, что сумка тоже является призом, а приз является сумкой вместительности 0. Чтобы перейти к таким обозначениям, сохранив задачу, надо прибавить 1 ко всем ai. Будем вести динамику вперед. Тогда из d[i][j][m] есть переход в d[i+1][j][m] c вероятностью p[i]/100, и в состояние d[i+1][j][m+a[i]] с вероятностью 1-p[i]/100. Ответ будет являться суммой d[n+1][j][m] по всем j,m таким что L ≤ j ≤ m + k. Это решение работает за 2004, и не укладывается в ограничение по времени.
Остается заметить, что если у нас есть более 200 мест, то не имеет значения сколько их именно. Это оставляет только состояния в которых m ≤ 200, и решение работает за 2003.
Задача 167C - Волшебники и числа Автор Alex-Gran.
Рассмотрим позицию (a,b). Пусть a < b. Из нее есть переход в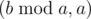 
. Рекурсивно определим является эта позиция выигрышной или проигрышной. Если она проигрышная, то наша (a,b) точно выигрышная. Иначе брать остаток по модулю точно никто не будет. Значит все будут вычитать степени меньшего из большего. Тогда осталось научится решать такую задачу. Можно вычитать неотрицательные степени a, проигрывает тот кто не может ходить. И решить ее для 
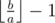. Эта задача решается так. Если a нечетное, то выигрышны все нечетные числа. Иначе выигрышны все числа, дающие нечетный остаток по модулю a+1, либо остаток -1 по тому же модулю. Это утверждение несложно доказывается по индукции. Приятным подарком является то, что условие для четных годится и для нечетных, потому что для нечетных оно просто эквивалентно нечетности числа.
Задача 167D - Волшебники и дороги Автор PavelKunyavskiy.
Эта была первая действительно сложная задача в контесте. Одной из сложностей было осознать условие :). Хочется надеяться, что мы смогли написать условие настолько понятно, насколько это было возможно в такой задаче.
Рассмотрим внимательно этот хитрый граф. В частности, рассмотрим внимательнее точку с наибольшим y.
1) Она соединена с самыми высокими точками слева и справа от нее.
2) Она не соединена со всеми остальными точками.
3) Она лежит во всех уголках на точках с разных сторон от нее.
Все эти три свойства достаточно отчетливо видны на рисунках.
Какие из этого можно сделать выводы.
1) Построения в левой и правой частях независимы.
2) Граф является деревом.
Раз граф является деревом, то максимальное паросочетание в нем можно искать либо жадно, либо простой динамикой. Но это работает за линейное время, чего явно не достаточно, чтобы ответить на все 105 запросов.
Впрочем, это не просто дерево! Те кто знают что это такое, наверное уже заметили, что оно декартово. Это позволяет выделять в нем дерево для подотрезка за время порядка высоты дерева, пересчитывая все нужные динамики.
И так как города строятся в случайных точках (а метод построения городов это гарантирует), то высота дерева O(K + logN).
Задача 167E - Волшебники и пари Автор Dmitry_Egorov.
В этой задаче речь шла про пути из истоков графа в стоки. На этим пути накладывалось условие, которое делало их зависимыми — они не должны были пересекаться по вершинам. Но в любой комбинаторике значительно проще жить, когда все независимо. Поэтому надо попытаться избавиться от условия про отсутствие пересечений по вершинам. Сделать это очень просто — забыть про него и все. Поймем почему ответ от этого не изменится: Пусть был какой-то набор путей в котором два пути пересекались. Покажем, что учтя этот путь мы заодно учтем и еще один лишний с противоположным знаком. Для этого поменяем продолжения у двух путей, которые пересекаются по вершине. Четность перестановки при этом поменялась, поэтому этот набор путей учитывается с противоположным знаком и в сумме они дают 0.
Что нам это дает? Если мы зафиксируем перестановку, то количество наборов путей, которым она соответствует равно произведению количеств путей для каждой пары сток-исток.
Пусть из i-го истока в j-ый сток существует cntij путей. Эта величина считается динамикой обходом в глубину.
Тогда ответ равен
. Такая сумма называется определитем матрицы cnt, который считается по модулю P методом Гаусса за O(S3), где S — количество стоков и истоков.
Еще надо было не забыть обработать изолированные вершины. Они либо не меняют ответ, либо домножают его на -1.
Осталось понять, что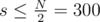 
, а 3003 прекрасно заходит в TL. Впрочем, аккуратно написанное решение за 6003 тоже проходило, так как работает столько же сколько решение Паши за 3003 на Java.
Формулы (задача B div 1) побились адски.
Все-таки не до конца ясен разбор B (Div. 2)...что означает "директива препроцессора"? Как при вводе с клавиатуры понять, что крайняя строка была последней?
это означает, что в строке первый не пробельный символ #
На С++ например так while (gets(s)) или whlie (scanf("%s", s) == 1) или while (cin>>s)
Эх, знать бы еще C++ :)
Приносим извинения. Это осталось с прошлой версии легенды — идея написать легенду про заклинания появилась в последний момент и разбор поправить не успели.
ЕМНИП, у дельфистов есть функция eof, а стандартные потоки ввода-вывода предопределены как переменные-файлы input и output.
Чтобы сымитировать конец файла с клавиатуры надо нажать Ctrl+Z. Тогда код, читающий с стандартного входа, поверит, что произошел EOF.
То же самое для Unix — Ctrl+D.
Косяк в задаче B div 1:
у вас рассматриваются различные переходы в одно и то же состояние.
UPD: исправили.
Div-1 B / Div-2 D. Можно поподробнее объянить как именно происходит переход в следующие состояния?
Мы либо выигрываем очередной контест, либо нет, третьего не бывает) Выигранный контест соответствует переходу в состояние d[i+1][j+1][m+a[i]] с вероятностью p[i]/100 (число мест увеличилось на a[i], число выигранный контестов на 1), а проигранный — в d[i+1][j][m] с вероятностью 1-p[i]/100.
Позже я выложу к каждой задаче ссылку на ее авторское решение, сейчас это невозможно технически.
d[i+1][j+1][m+a[i]] *= d[i][j][m] * p[i] / 100;
d[i+1][j][m] *= d[i][j][m] * (100 — p[i]) / 100;
так я понимаю или нет? или надо суммировать, а не умножать? а если суммировать то вроде бы надо делить на с каким количеством способов мы пришли в это состояние...
нет не так, += а не *=
Надо суммировать, причем просто суммировать, без всяких делений.
Только у нас получается что при выигрыше сумки, мы тратим один слот впустую (как будто для сумки нужна сумка), а это вроде как неправильно. Или я неправ?
Не правда. Мы считаем сколько у нас будет места плюс к тому что есть.
это -1 или +размер_сумки, т.е данные вводтся ровно как хочется
А, понял, спасибо.
Ок. С этими переходами я согласен, но то что написано в разборе не сходится с этим комментарием. Так и должно быть ?
Would you please submit writers' solutions on Codeforces? So we can learn from the code.
Что с тестированием, настолько медленного и унылого тестирования давно не видел.
к хорошему быстро привыкаешь)
не наоборот? и почему j никогда не увеличивается?
Там опечатка. Должно быть так: "...из d[i][j][m] есть переход в d[i+1]**[j+1]**[m] c вероятностью p[i]/100..." Так как после долгих раздумий становится понятно, что если мы выиграли очередной тур, то количество выигранных туров увеличивается.
Срочно нужен КЭП.
почему падает это решение ?
задача А div 2.
убери long long и попробуй отправить...
почему-то тоже так кажется. а косяк в чем?
да нет же, твое решение падает на тесте: 12 2 50, выводит 5, а надо 4, как я понимаю
да, опечатка. капец до 13 теста дошла. X с Y перепутала. ну я лох...
Спасибо за задачу С (div I), понравилась. Единственное что не понравилось — что задача С была слишком малостоящей. То есть быстро решить В, не запоровшись с double, было намного выгоднее, чем к концу контеста решить С.
In B-DIV-1, Those who missed min(200, now + a[i]) and used now + a[i], and got WA on test-27, minus this post.
Подскажите пожалуйста, почему падает это решение по С Div2,которое по идее полностью совпадает с разборным.
Подскажите, почему может получать TL вот эта посылка: 1430997 (задача C div2) . Все сделано как в разборе, ничего лишнего нет, то же самое на C++ отрабатывает.
java.util.Scannerтакой медленный, что за то время, пока он читает инпут, tourist решает задачу.Div2 B, Wrong answer on test 20
Checker Log wrong answer Eoln expected, EOF found(line 1575,character 0)
What does it mean?
You need EOLN( i.e "\n"), and maybe text after it, but your answer is ended
Maybe you print less lines than needed
Probably that you are not outputting the last end of line character under some conditions.
Thanks all. Got it.
I used in.hasNext() before. Once I changed it to in.hasNextLine(), it passed.
Not very sure about the difference for this test case.
Скажите пожалуйста,можно ли как — нибудь узнать, что за тест 41, задачи A/Div2 ?
Зайти в свои посылки. Кликнуть на номер интересующей посылки
7878 4534 9159В задаче С (div2) Не сразу въехал, почему на первом же претесте WA, при правильном ответе. Оказалось, на Delphi не проходят действительные числа в виде (FormatFloat('0.#####'), x). Интересно, почему? Потому что в качестве разделителя выступает запятая вместо точки?
Нужно выводить "."
То есть да, перепутал, formatfloat выводит запятую, вместо точки. Значит в этом дело, спасибо.
<Задача B div 2. TL на тесте 35> Программа, если запускать exe, не находит конец файла. Если запускать из-под компилятора, то все нормально. Почему? http://codeforces.me/contest/168/submission/1428329
168A, it was necessary not to forget avoid division by 0, when Y = 0, you should correct the post, because the problem statement says Y >= 1
In Problem B of Div 1, why this case has the right answer of 0.93 not 1.0 ?
1 0 0
7
-1
In my opinion, we can always perform well in 0 round whatever the result of the first tour is, is that correct ? Thanks!
During the contest my opinion is same with yours. But now I understand .In this problem ,the one must play all the tours. then at all , if he won at least l and he can take all prices back home ,it will be consider perfect. So in this case , if he won he can't take the price home so isn't perfect, But if he lost , it will be consider perfect...
Thanks for your comments. However, I still have a silly question. If we only consider perfect win, why the sample input
3 1 0
10 20 30
-1 -1 2
gives 0.3? The only valid way is to lose the first two rounds and win the last one, of which the probability is 0.9 * 0.8 * 0.3 ?In that case last round's award — bag of size 2 compensates first two rounds, so if you win in the last round you can do whatever you want on first two, because now you have bag which can carry all other awards.
Thank you. This makes sense now.
I approached the problem the same way you did — I assumed that I can carry a "huge prize" after a tour win only if I have room in bags for it at that point. I got 0.216 for that case as well.
The worst part is that I tried to fix my code to produce 0.3 still maintaining the same assumption. It took me a while to realize that all it matters is to have enough room in bags after all tours.
Now when I read the statement I am not sure how I misunderstood it, but a lot of other people did — maybe the explanation of the sample should have been a bit more verbose.
Exactly! I always think that I should be able to take all the prize home right after each round... Thank you!
Can somebody throw more light on solution for 167C - Wizards and Numbers as to how one obtains the relation to solve the subproblem of subtracting a non-negative degree of smaller number from the larger one?
Let's say the larger number is B, the smaller one is A. If A is odd, the case is pretty simple -- after each turn B % 2 changes, so we win if and only if B%2 = 0.
If A is even, we win if B % (A+1) is even. To prove it we need to prove that each winning state has a move to a losing state, and that any move from the losing state only goes to a winning state.
If B % (A+1) is even, we can always make it odd by subtracting one, if B % (A+1) is not zero, or by subtracting A, if it is zero. That proves that from every winning state there's a move into a losing state.
If B % (A+1) is odd, any turn will make it odd. This can be proven by induction: If you subtract A^0=1, B % (A+1) will obviously become even. Let's say we have proven that subtracting A^k changes oddness. Since subtracting A^k * (A+1) obviously doesn't change oddness (since it is divisible by A+1), subtracting A^(k+1) = A^k * (A+1) — A^k does change it. That proves that from any losing state you can only move to a winning state.
Thanks,I got that..,but I am still confused as the two moves(b->bmoda && b-a^k) are being taken independently to solve the problem.I mean after changing b->bmoda one can take b->b-a^k so why is that not being considered?
Actually you can prove that every turn B % (A+1) must change odd/even, because you can only take A^k for some k>=0, and it is A^k = (A+1 -1)^k = p*(A+1) + (-1)^k which is +1 or -1 when mod (A+1). In the end it is zero, so you win iff B % (A+1) is even. See rng_58's solution.
+/-1 in general doesn't change odd/even for B%(A+1), if A is even. If B%(A+1) = 0, then (B-1)%(A+1) = A -- oddness doesn't change.
thanks for pointing the error. The statement should read: let m = B % (A+1) if m is even, then there is a move that will make it to odd else m is odd, then every move will make it even
Proof: If m is even, then either m=0 or m>0 for m=0, we can take a move of A, then m become B-A = 1 mod (A+1) it is odd for m>0, we can take a move of 1, then m become B-1 = even-1 = odd mod (A+1)
If m is odd, then any move is of the form A^k = (A+1 -1)^k = (-1)^k mod (A+1) So after the move m become odd — (-1)^k = even mod (A+1)
If %(a+1),I can get accepted but what's wrong with %(a-1) (a-1>1) ? It get wa when test b=449843221913123719 a=16 (test 3)
Let's define function F[x]={0,1}: when stat x can make first win F[x]=0,else F[x]=1;
if F[x]=0,there must be a k (k>=0&&b-a^k>=0) makes F[x-a^k]=1;
if F[x]=1,for all k (k>=0&&b-a^k>=0) F[x-a^k]=0;
When F[x]=(x%(a-1))&1.
if F[x]=0. x%(a-1) must be a even,and for all k:
(x-a^k)%(a-1) =x%(a-1) — (a^k)%(a-1) =even + odd= odd
if F[x]=1. x%(a-1) must be a odd,and for all k:
(x-a^k)%(a-1) =x%(a-1) — (a^k)%(a-1) =odd + odd= even
so F[x]=(x%(a-1))&1 satisfy two condition above. What's wrong with this function? Please tell me ,Thx!
(double post)
Подскажите, пожалуйста. Где здесь ошибка? 1427901
UPD: все, нашел ошибку.
in 168b, if the input is
#
#
how should the output is ? i think the right is :
#
#
but my code generate:
#
#
and it's accepted (even if tested after the contest), because that kind of test case is not appear,
the test case itself is just 11, if possible, add hacking after contest too
sry for my bad english
I'll tell you big secret: we can't see difference between your three test datas.
i mean, if the input is #(two new line)#, the output in my mind is supposedly #(two new line)#, but my code generate #(one new line)# and accepted
what is the right answer for that ? thx for the reply
From the problem statement: Note that empty lines must be processed just like all the others: they must be joined to the adjacent non-amplifying lines, or preserved in the output, if they are surrounded with amplifying lines on both sides (i.e. the line above it, if there is one, is amplifying, and the line below it, if there is one, is amplifying too).
So, two consecutive empty lines should be joined into one.
Why answer for the first test is 0.3 ?
3 1 0
10 20 30
-1 -1 2
we need to lose first two days (the probabily of this event is 0.9 * 0.8) and win 3 day so finish probability is 0.9 * 0.8 * 0.3
and in pretests 5 we have
1 0 0
7
-1
so the probability that we lose first day is 0.93 and this is the answer.
I can't understand if we don't count lose probabily in example test, why we need to count it in pretest 5?
Thanks
You don't have to lose first two games. If you win the third game, you will have a bag big enough to fit any presents from first two days, should you win any.
I can't not understand the problem description because of my poor English... What a easy problem , however, so little people got accepted...
Div2 B..
Можно ли решить Bdiv1 динамикой назад, а не вперед? Скорее всего, там придется отдельно рассматривать случай dp[i][j][200+].
Можно и назад. Только для элемента, который "200+", для случая, если в данном туре победили, будет прибавляться не какой-то 1 элемент с предыдущего шага, а сразу сумма dp[i-1][j-1][200-a[i]]...dp[i-1][j-1][200] (все эти случаи дадут нам 200+). А остальное по-обычному, четкие переходы с элемента в элемент, все понятно и принципиально не отличается от динамики вперед.
Я больше никогда не буду писать рекурсивную динамику, если можно написать прямую.
Я больше никогда не буду писать рекурсивную динамику, если можно написать прямую.
Я больше никогда не буду писать рекурсивную динамику, если можно написать прямую.
Я больше никогда не буду писать рекурсивную динамику, если можно написать прямую.
Я больше никогда не буду писать рекурсивную динамику, если можно написать прямую.
P.S. Спасибо, понял, почему не работало. Потерял на этом минут 15-20, как следствие не успел решить C и полностью слил раунд.
Thanks!
What's the expected output format of test case 3 for div2 B? My result has 4 lines and 2 characters as described:
newline
# with newline
newline
# with newline
I got a error saying "expected EOLN" but didn't find out any bug myself. Can someone help me?
What you mentioned is not what you are printing to the output. Look at the judgement protocol carefully. The third line has two spaces in the input and you are printing these two spaces in the output as well instead of removing them — you can see that when you mark the lines. So the judge is expecting an EOLN but finds a space instead.
why is my comment written with so big letters ?
You can edit your post. Instead of pasting your code, you could give the link to it (you can retrieve the link by clicking the upper right "#" when you open the code).
Anyway, on Codeforces you can't use the function
system(), just delete it before submitting the code!For some reason, I am not able to see the codes of "168B — Wizards and Minimal Spell". Even I can't see my own code!! I've got "Wrong Answer of Test 1" verdict btw.
Am I the only one facing this problem?
In problem 167B — Wizards and Huge Prize editorial, it says "The answer will be the sum of $$$d[n+1][j][m]$$$ for all $$$j,m$$$ such ...".
I have the question about this: What if there are some $$$d[n + 1][j + 1][m + ...]$$$ that will include $$$d[n + 1][j][m]$$$ (What I means is they are not distinct to each other), so can we just sum all of them so simply like that?.
I learned that: Only if all the events A, B, C, .. are pairwise distinct, $$$P(A + B + C + ...) = P(A) + P(B) + P(C) + ...$$$. So how are all the $$$d[n + 1][j][m]$$$ are pairwise distinct anyway?
Sorry for my bad English, thanks for reading <3 <3.
Anybody can help me :<< ?
Any..body kind in this awesome Codeforces community :< ?
I suspect the reason nobody has answered so far is that nobody has looked at this editorial for about 3 years.
d[n+1][j][m] is the probability that, at the end, you have won exactly j contests, and have exactly m bags. You can't have won both exactly j and exactly k contests unless j and k are equal, and you can't have exactly m1 and exactly m2 bags unless m1 and m2 are equal, so these events are clearly distinct from each other.
Thank you for clarify it out <3 <3. At first, I was thinking $$$d[n + 1][j + 1][m + X]$$$ can include $$$d[n + 1][j][m]$$$ somehow but it turned out to be wrong.
Love you <3 for answering my question.
Can someone please explain the part
For convenience, we assume that the bag is also a prize and the prize is a bag of capacity 0. To do that, retaining a task we must add 1 to all a[i]in div1 B's editorial ?d[i][j][m] is the probability that, you have participated in contests of first 'i' days , you have won exactly j contests, and have exactly m bags. Now this m is the total capacity you gain after all the contests.
So if we assume a prize is a bag, it will not contribute to the overall capacity. Since a[i]=-1, we add one to make it zero and from d[i][j][m] we can go to the d[i+1][j+1][m+a[i]] (capacity remains then same if we win a prize),
Now we are also assuming bag is a prize and going from d[i][j][m] to the d[i+1][j+1][m+a[i]] state meaning, we are increasing j(the number of prizes won) and assigning that extra capacity ( a[i]+ '1' (this one)). to the bag we considered as a prize. Increasing j here means we considered bag as a prize so we increase the bag capacity by one to accommodate the same bag we considered as a prize.
Problem E is as the same as a well-known lemma: Lindström–Gessel–Viennot lemma