Введение
После окончания Codeforces Beta Round #11 несколько участников захотели почитать что нибудь о задачах, похожих на задачу D этого раунда. Автор статьи, в целях помочь этим участникам, попытался найти подобную информацию, однако был удивлен, что ничего путного в интернете нет. Неизвестно, то ли автор плохо искал, то ли это действительно так, однако (на всякий случай), он решил написать собственную статью на эту тему.
В некотором смысле эту статью можно рассматривать как разбор задачи D 11го бета раунда.
В данной статье рассмотрены довольно известные алгоритмы поиска оптимальных гамильтоновых путей и циклов, а так же подсчет их количества, проверки существования и еще кое что. В качестве метода используется так называемый метод "динамика по подмножествам". Данный метод работает экспоненциальное время и использует экспоненциальный объем памяти от размерности графа. Поэтому применим только если граф очень маленький - как правило не более 20 вершин.
Динамика по подмножествам
Рассмотрим множество элементов, занумерованных от 0 до N - 1. Каждое подмножество этого множества можно закодировать последовательностью битов длины N (эту последовательность будем называть маской). Если i-й бит маски равен 1, то i-й элемент входит в подмножество, иначе - нет. Например, маска 00010011 означает, что в подмножестве находятся элементы 0, 1 и 4 из множества [0... 7]. Всего получается 2N масок, задающих 2N подмножеств. Каждая маска по сути является целым числом, записанном в двоичной системе счисления.
Метод состоит в том, чтобы каждой маске (а значит и каждому подмножеству) сопоставлять какое либо значение и, на основе уже просчитанных значений для некоторых масок, получать значения для других масок. Как правило, в процессе просчета из текущего подмножества A извлекается один элемент всеми допустимыми способами и из полученных подмножеств A1', A2', ... , Ak' получается значение для A. Однако для этого все значения для Ai' уже должны быть вычислены. Поэтому требуется установить порядок, в котором будут просматриваться маски. Несложно понять, что перебор масок в порядке возрастания чисел, которыми и являются эти маски, нам подойдет.
Для дальнейшего повествования примем следующие обозначения:
bit(i, mask) - i-й бит маски mask
count(mask) - количество битов 1 в маске mask
first(mask) - наименьший номер бита 1 в маске mask
(a?b: c) - возвратить b если выполняется a, или возвратить c в противном случае.
Элементами множества будут являться вершины графа. Для простоты мы будем считать, что граф является неориентированным. Модификация нижеприведенных алгоритмов для случая ориентированного графа предоставляется читателю.
1. Нахождение кратчайшего гамильтонова пути
Пусть в графе G = (V, E) n вершин и каждое ребро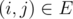 имеет некоторый вес d(i, j). Необходимо найти гамильтонов путь, сумма весов по ребрам которого минимальна.
имеет некоторый вес d(i, j). Необходимо найти гамильтонов путь, сумма весов по ребрам которого минимальна.
Пусть dp[mask][i] обозначает длину кратчайшего гамильтонова пути подмножества вершин mask, заканчивающегося в вершине i.
Динамика считается по следующим соотношениям:
dp[mask][i] = 0, если count(mask) = 1 и bit(i, mask) = 1;
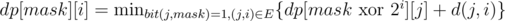 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;
dp[mask][i] = ∞ во всех остальных случаях.
Теперь искомая минимальная длина пути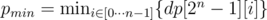 . Если pmin = ∞, то гамильтонова пути в графе, увы, нет. Восстановить сам путь несложно. Пусть минимальный путь заканчивается в вершине i. Тогда j ≠ i, для которого
. Если pmin = ∞, то гамильтонова пути в графе, увы, нет. Восстановить сам путь несложно. Пусть минимальный путь заканчивается в вершине i. Тогда j ≠ i, для которого 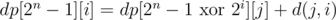 , является предыдущей вершиной пути. Теперь удалим i из множества и только что описанным способом найдем вершину предыдущую к j. Продолжая процесс пока не останется одна вершина, мы найдем весь гамильтонов путь.
, является предыдущей вершиной пути. Теперь удалим i из множества и только что описанным способом найдем вершину предыдущую к j. Продолжая процесс пока не останется одна вершина, мы найдем весь гамильтонов путь.
Данное решение требует O(2nn) памяти и O(2nn2) времени.
2. Нахождение количества гамильтоновых путей
Пусть теперь у нас есть невзвешенный граф G = (V, E). Модифицируем предыдущий алгоритм. Пусть dp[mask][i] теперь означает количество гамильтоновых путей подмножества mask, заканчивающихся в вершине i. Динамика перепишется следующим образом:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;
dp[mask][i] = 0 во всех остальных случаях.
Ответом будет число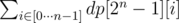 .
.
Решение требует O(2nn) памяти и O(2nn2) времени.
3. Нахождение количества простых цепей
Посчитаем динамику, указанную в предыдущем пункте. Ответом будет являться число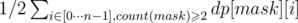 . Коэффициент 1 / 2 необходим, поскольку каждую цепь мы учитываем 2 раза - в одном и обратном направлении. Так же следует отметить, что тут учтены только пути длины хотя бы 1. При желании можно к ответу добавить n путей длины 0.
. Коэффициент 1 / 2 необходим, поскольку каждую цепь мы учитываем 2 раза - в одном и обратном направлении. Так же следует отметить, что тут учтены только пути длины хотя бы 1. При желании можно к ответу добавить n путей длины 0.
Данное решение требует O(2nn) памяти и O(2nn2) времени.
4. Проверка существования гамильтонова пути
Тут можно обойтись решением 2, заменив сумму на побитовое ИЛИ. Тогда dp[mask][i] будет содержать булево значение - существует ли в подмножестве mask гамильтонов путь, заканчивающийся в вершине i. Сама динамика будет такая:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
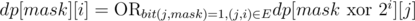 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;
dp[mask][i] = 0 во всех остальных случаях.
Это решение, как и решение 2, требует O(2nn) памяти и O(2nn2) времени. Эту оценку можно улучшить, если изменить динамику следующим образом.
Пусть dp'[mask] хранит маску подмножества всех вершин, для которых существует гамильтонов путь в подмножестве mask, заканчивающихся в этой вершине. Другими словами, сожмем предыдущую динамику: dp'[mask] будет равно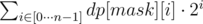 . Для графа G выпишем n масок Mi, для каждой вершины задающие множество вершин, которые связаны ребром в данной вершиной. То есть
. Для графа G выпишем n масок Mi, для каждой вершины задающие множество вершин, которые связаны ребром в данной вершиной. То есть 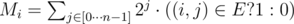 .
.
Тогда динамика перепишется следующим образом:
dp'[mask] = 2i, если count(mask) = 1 и bit(i, mask) = 1;
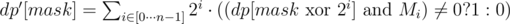 , если count(mask) > 1;
, если count(mask) > 1;
dp'[mask] = 0 во всех остальных случаях.
Особое внимание следует уделить выражению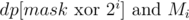 . Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве mask без вершины i, а вторая - подмножество вершин, связанных с i ребром. Если эти множества пересекаются хотя бы по одной вершине (их and не равен 0), то, как нетрудно понять, в mask существует гамильтонов путь, заканчивающийся в вершине i.
. Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве mask без вершины i, а вторая - подмножество вершин, связанных с i ребром. Если эти множества пересекаются хотя бы по одной вершине (их and не равен 0), то, как нетрудно понять, в mask существует гамильтонов путь, заканчивающийся в вершине i.
Окончательная проверка состоит в сравнении dp[2n - 1] c 0.
Это решение использует O(2n) памяти и имеет асимптотику O(2nn).
5. Нахождение кратчайшего гамильтонова цикла
Поскольку нам безразлично с какой вершины начинаться цикл, пусть он начинается с вершины 0. Далее, воспользуемся решением 1 для подмножества вершин, видоизменив соотношения следующим образом:
dp[1][0] = 0;
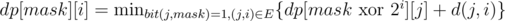 , если i > 0, bit(0, mask) = 1 и bit(i, mask) = 1;
, если i > 0, bit(0, mask) = 1 и bit(i, mask) = 1;
dp[mask][i] = ∞ во всех остальных случаях.
Таким образом, dp[mask][i] будет содержать длину кратчайшего гамильтонова пути от вершины 0 до вершины i.
Искомый минимум нужно будет выбирать по формуле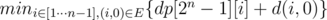 . Если полученный минимум равен ∞, то искомого цикла не существует. Искомый цикл восстанавливается аналогично решению 1.
. Если полученный минимум равен ∞, то искомого цикла не существует. Искомый цикл восстанавливается аналогично решению 1.
6. Нахождение количества гамильтоновых циклов
Используя идеи решений 5 и 2, можно получить динамику, считающую количество гамильтоновых циклов за время O(2nn2), использующее O(2nn) памяти.
7. Нахождение количества простых циклов
Пусть dp[mask][i] означает количество гамильтоновых путей в подмножестве вершин mask, начинающихся в вершине first(mask) и заканчивающихся в вершине i. Переход динамики выглядит так:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
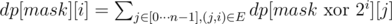 , если count(mask) > 1, bit(i, mask) = 1 и i ≠ first(mask);
, если count(mask) > 1, bit(i, mask) = 1 и i ≠ first(mask);
dp[mask][i] = 0 иначе.
Ответом будет являться сумма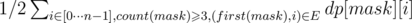 .
.
Это решение за время O(2nn2) и память O(2nn).
8. Проверка существования гамильтонова цикла
Модифицируем решение 5 и, воспользовавшись приемом, описанном в решении 4, получим решение для этой задачи за время O(2nn) и память O(2n).
Упражнения
CFBR11D
CCTOOLS
P.S. Эта статья в будущем, возможно, будет дополняться и исправляться. Автор будет благодарен за пополнение раздела упражнений ссылками на задачи из архивов, а так же на найденные ошибки и неточности.
После окончания Codeforces Beta Round #11 несколько участников захотели почитать что нибудь о задачах, похожих на задачу D этого раунда. Автор статьи, в целях помочь этим участникам, попытался найти подобную информацию, однако был удивлен, что ничего путного в интернете нет. Неизвестно, то ли автор плохо искал, то ли это действительно так, однако (на всякий случай), он решил написать собственную статью на эту тему.
В некотором смысле эту статью можно рассматривать как разбор задачи D 11го бета раунда.
В данной статье рассмотрены довольно известные алгоритмы поиска оптимальных гамильтоновых путей и циклов, а так же подсчет их количества, проверки существования и еще кое что. В качестве метода используется так называемый метод "динамика по подмножествам". Данный метод работает экспоненциальное время и использует экспоненциальный объем памяти от размерности графа. Поэтому применим только если граф очень маленький - как правило не более 20 вершин.
Динамика по подмножествам
Рассмотрим множество элементов, занумерованных от 0 до N - 1. Каждое подмножество этого множества можно закодировать последовательностью битов длины N (эту последовательность будем называть маской). Если i-й бит маски равен 1, то i-й элемент входит в подмножество, иначе - нет. Например, маска 00010011 означает, что в подмножестве находятся элементы 0, 1 и 4 из множества [0... 7]. Всего получается 2N масок, задающих 2N подмножеств. Каждая маска по сути является целым числом, записанном в двоичной системе счисления.
Метод состоит в том, чтобы каждой маске (а значит и каждому подмножеству) сопоставлять какое либо значение и, на основе уже просчитанных значений для некоторых масок, получать значения для других масок. Как правило, в процессе просчета из текущего подмножества A извлекается один элемент всеми допустимыми способами и из полученных подмножеств A1', A2', ... , Ak' получается значение для A. Однако для этого все значения для Ai' уже должны быть вычислены. Поэтому требуется установить порядок, в котором будут просматриваться маски. Несложно понять, что перебор масок в порядке возрастания чисел, которыми и являются эти маски, нам подойдет.
Для дальнейшего повествования примем следующие обозначения:
bit(i, mask) - i-й бит маски mask
count(mask) - количество битов 1 в маске mask
first(mask) - наименьший номер бита 1 в маске mask
(a?b: c) - возвратить b если выполняется a, или возвратить c в противном случае.
Элементами множества будут являться вершины графа. Для простоты мы будем считать, что граф является неориентированным. Модификация нижеприведенных алгоритмов для случая ориентированного графа предоставляется читателю.
1. Нахождение кратчайшего гамильтонова пути
Пусть в графе G = (V, E) n вершин и каждое ребро
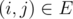 имеет некоторый вес d(i, j). Необходимо найти гамильтонов путь, сумма весов по ребрам которого минимальна.
имеет некоторый вес d(i, j). Необходимо найти гамильтонов путь, сумма весов по ребрам которого минимальна.Пусть dp[mask][i] обозначает длину кратчайшего гамильтонова пути подмножества вершин mask, заканчивающегося в вершине i.
Динамика считается по следующим соотношениям:
dp[mask][i] = 0, если count(mask) = 1 и bit(i, mask) = 1;
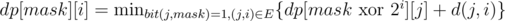 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;dp[mask][i] = ∞ во всех остальных случаях.
Теперь искомая минимальная длина пути
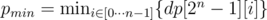 . Если pmin = ∞, то гамильтонова пути в графе, увы, нет. Восстановить сам путь несложно. Пусть минимальный путь заканчивается в вершине i. Тогда j ≠ i, для которого
. Если pmin = ∞, то гамильтонова пути в графе, увы, нет. Восстановить сам путь несложно. Пусть минимальный путь заканчивается в вершине i. Тогда j ≠ i, для которого 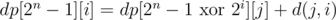 , является предыдущей вершиной пути. Теперь удалим i из множества и только что описанным способом найдем вершину предыдущую к j. Продолжая процесс пока не останется одна вершина, мы найдем весь гамильтонов путь.
, является предыдущей вершиной пути. Теперь удалим i из множества и только что описанным способом найдем вершину предыдущую к j. Продолжая процесс пока не останется одна вершина, мы найдем весь гамильтонов путь.Данное решение требует O(2nn) памяти и O(2nn2) времени.
2. Нахождение количества гамильтоновых путей
Пусть теперь у нас есть невзвешенный граф G = (V, E). Модифицируем предыдущий алгоритм. Пусть dp[mask][i] теперь означает количество гамильтоновых путей подмножества mask, заканчивающихся в вершине i. Динамика перепишется следующим образом:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;dp[mask][i] = 0 во всех остальных случаях.
Ответом будет число
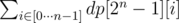 .
.Решение требует O(2nn) памяти и O(2nn2) времени.
3. Нахождение количества простых цепей
Посчитаем динамику, указанную в предыдущем пункте. Ответом будет являться число
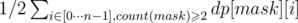 . Коэффициент 1 / 2 необходим, поскольку каждую цепь мы учитываем 2 раза - в одном и обратном направлении. Так же следует отметить, что тут учтены только пути длины хотя бы 1. При желании можно к ответу добавить n путей длины 0.
. Коэффициент 1 / 2 необходим, поскольку каждую цепь мы учитываем 2 раза - в одном и обратном направлении. Так же следует отметить, что тут учтены только пути длины хотя бы 1. При желании можно к ответу добавить n путей длины 0.Данное решение требует O(2nn) памяти и O(2nn2) времени.
4. Проверка существования гамильтонова пути
Тут можно обойтись решением 2, заменив сумму на побитовое ИЛИ. Тогда dp[mask][i] будет содержать булево значение - существует ли в подмножестве mask гамильтонов путь, заканчивающийся в вершине i. Сама динамика будет такая:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
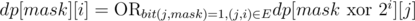 , если count(mask) > 1 и bit(i, mask) = 1;
, если count(mask) > 1 и bit(i, mask) = 1;dp[mask][i] = 0 во всех остальных случаях.
Это решение, как и решение 2, требует O(2nn) памяти и O(2nn2) времени. Эту оценку можно улучшить, если изменить динамику следующим образом.
Пусть dp'[mask] хранит маску подмножества всех вершин, для которых существует гамильтонов путь в подмножестве mask, заканчивающихся в этой вершине. Другими словами, сожмем предыдущую динамику: dp'[mask] будет равно
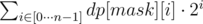 . Для графа G выпишем n масок Mi, для каждой вершины задающие множество вершин, которые связаны ребром в данной вершиной. То есть
. Для графа G выпишем n масок Mi, для каждой вершины задающие множество вершин, которые связаны ребром в данной вершиной. То есть 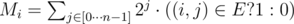 .
.Тогда динамика перепишется следующим образом:
dp'[mask] = 2i, если count(mask) = 1 и bit(i, mask) = 1;
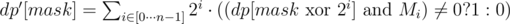 , если count(mask) > 1;
, если count(mask) > 1;dp'[mask] = 0 во всех остальных случаях.
Особое внимание следует уделить выражению
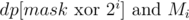 . Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве mask без вершины i, а вторая - подмножество вершин, связанных с i ребром. Если эти множества пересекаются хотя бы по одной вершине (их and не равен 0), то, как нетрудно понять, в mask существует гамильтонов путь, заканчивающийся в вершине i.
. Первая часть выражения содержит подмножество вершин, для которых существует гамильтонов путь, заканчивающихся в соответствующих вершинах в подмножестве mask без вершины i, а вторая - подмножество вершин, связанных с i ребром. Если эти множества пересекаются хотя бы по одной вершине (их and не равен 0), то, как нетрудно понять, в mask существует гамильтонов путь, заканчивающийся в вершине i.Окончательная проверка состоит в сравнении dp[2n - 1] c 0.
Это решение использует O(2n) памяти и имеет асимптотику O(2nn).
5. Нахождение кратчайшего гамильтонова цикла
Поскольку нам безразлично с какой вершины начинаться цикл, пусть он начинается с вершины 0. Далее, воспользуемся решением 1 для подмножества вершин, видоизменив соотношения следующим образом:
dp[1][0] = 0;
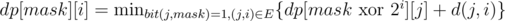 , если i > 0, bit(0, mask) = 1 и bit(i, mask) = 1;
, если i > 0, bit(0, mask) = 1 и bit(i, mask) = 1;dp[mask][i] = ∞ во всех остальных случаях.
Таким образом, dp[mask][i] будет содержать длину кратчайшего гамильтонова пути от вершины 0 до вершины i.
Искомый минимум нужно будет выбирать по формуле
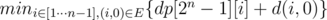 . Если полученный минимум равен ∞, то искомого цикла не существует. Искомый цикл восстанавливается аналогично решению 1.
. Если полученный минимум равен ∞, то искомого цикла не существует. Искомый цикл восстанавливается аналогично решению 1.6. Нахождение количества гамильтоновых циклов
Используя идеи решений 5 и 2, можно получить динамику, считающую количество гамильтоновых циклов за время O(2nn2), использующее O(2nn) памяти.
7. Нахождение количества простых циклов
Пусть dp[mask][i] означает количество гамильтоновых путей в подмножестве вершин mask, начинающихся в вершине first(mask) и заканчивающихся в вершине i. Переход динамики выглядит так:
dp[mask][i] = 1, если count(mask) = 1 и bit(i, mask) = 1;
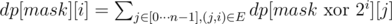 , если count(mask) > 1, bit(i, mask) = 1 и i ≠ first(mask);
, если count(mask) > 1, bit(i, mask) = 1 и i ≠ first(mask);dp[mask][i] = 0 иначе.
Ответом будет являться сумма
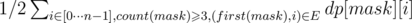 .
.Это решение за время O(2nn2) и память O(2nn).
8. Проверка существования гамильтонова цикла
Модифицируем решение 5 и, воспользовавшись приемом, описанном в решении 4, получим решение для этой задачи за время O(2nn) и память O(2n).
Упражнения
CFBR11D
CCTOOLS
P.S. Эта статья в будущем, возможно, будет дополняться и исправляться. Автор будет благодарен за пополнение раздела упражнений ссылками на задачи из архивов, а так же на найденные ошибки и неточности.











For example
пусть пока повисит тут. потом, возможно, добавлю. возможно в новый раздел:)
только, боюсь, оно большое, страшное и представляет из себя чисто теоретический интерес:) то есть для олимпиад совершенно непригодное
Maybe I will view your problem in fiture article:)
it is very old paper:)
У меня только одна мелкая корректировка, в п.5 вместо этого:
по-моему, правильнее будет вот это (особенно, если граф ориентированный):
про циклы на сетке где-то выше уже была ссылка:
http://www.cs.ust.hk/mjg_lib/Library/Kwong_Ham_94.pdf
конечно, если вдруг и существует подобный архив, мне самому было бы интересно на него взглянуть:)
про дп по ломаному профилю я бы тоже хотел почитать если кто поделится ссылкой:)
по поводу можно ли решать за полином по времени - это вопрос задачи P vs NP. поэтому еще никто этого не знает. вот недавно появилась попытка доказать что таки P!=NP)) сами же задачи, которые я рассмотрел, относятся к классу NP в общем случае.
если нужен полином по памяти - backtracking вам в руки:) правда время выполнения тут несколько увеличивается и остается экспоненциальным.
Многие задачи принадлежат классу #P что конечно не тоже самое что NP.
is an example problem for part 5.
будем итеративно выполнять следующий процесс:
для пары соседних точек A->B, не соединенных ребром найдем такую пару C->D, что имеются ребра AC и BD. такая пара всегда найдется из-за того, что граф Дирака (ну, там по принципу Дирихле можно доказать). теперь все точки от B до D перезаписываем в обратном порядке (дугу как бы переворачиваем).
рано или поздно процесс остановится и на окружности мы получим гамильтонов цикл. почему это так: на каждой итерации мы увеличиваем количество ребер на окружности хотя бы на единицу. поскольку мы увеличиваем хотя бы на константу (это важно), а максимальное количество ребер n,
то не более чем через n итераций процесс закончится.
итого - алгоритм за O(n*n), для 1000 вершин все замечательно:)
в предыдущий комментарий, вероятно, закралась опечатка.
правильно "теперь все точки от B до C перезаписываем в обратном порядке (дугу как бы переворачиваем)."
Could you please further explain the recurrence in the first example (finding a shortest Hamiltonian walk)?
The following paper is potentially useful as reference:
"A Dynamic Programming Approach to Sequencing Problems" by Michael Held and Richard M. Karp, 1962. [citation, download]
It contains lots of preliminary analysis and at least the DP approaches described in 1. and 5. of your post. I believe the algorithm is actually called "Held–Karp algorithm" in academic literature, but it was described independently by Bellman et al. in another paper.
A list of optimal algorithms for TSP with better runtime complexity can be found here.
can't open first link it requires e-mail for link sites.can u help me and give pdf file?
Took me two seconds to find another PDF source: http://people.cs.vt.edu/~gback/ICPCHandbook/book/copiesfromweb/held-karp-jsiam-1962.pdf
you're welcome.
In 4th section's second dp formulation second part, the condition stated is count(mask)>1 only. Isn't bit(mask, i) == 1 condition should also be included?
can anybody give me link to its implemented code for any of the above part. Rest I got stuck at bit masking in implementation. Thanks in advance whoever will give link.
My solution for task D of CF beta round 11.
Btw,am i the only one who can't see the solution of others in this contest?i can't even open my solution.
me too, something is wrong today, I can't open submission code, including myself, now I can only open my "official" submissions.
Yes also just encountered this problem. Why I try to open my own solution I get "You are not allowed to view the requested page" error.
I actually have theory now for why this is. I think problem D might have been used in the VK Cup Finals — Trial Contest, and so they blocked solutions so we could not see submission from people in that contest.
In first Section, consider a graph with only two vertices and one edge of weight say w then the answer computed by the process, comes to be w but expected asnwer is 2*w as for a hamiltonian walk the starting and ending vertices must be same.
In the 7th section, how are those paths included in the answer where we use vertices v < first(mask). This means, if our bit representation of mask is 1101000, and we want to count no. of paths starting at first(mask)=3(3rd bit, 0-based indexing from right to left) and ending at vertex v=5(0-based indexing from right to left), how will paths like the one starting from vertex 3 to vertex 5 with vertex 0 on the way(and similar) be counted if we use the dp meaning given in section 7?
In a hamiltonian walk the vertices might repeat. On the other hand, in a simple path repetition of vertices is not allowed. How is it that using the same dp for ques 3 which was used for ques 2 works? Any insights would be highly appreciated.
i think it is actually hamiltonian 'path' and not hamiltonian 'walk'.
Isn't checking for hamiltonian path obvious when atleast 2 nodes are attached to each other?
Great Post. Cleared all the doubts regarding "Hamiltonian". Thanks a lot.
in problem 2, is the graph complete?
I think in the first two problem author is talking about Hamiltonian path, not about Hamiltonian walk. Please correct me if I am wrong. Thanks!
I think so.
Как в сэмпле задачи 11D - Простая задача получилось 7 простых циклов?
1-2-3
1-2-4
1-3-4
2-3-4
1-2-3-4
где ещё два цикла?
Link to HackerEarth practice problems.
I noticed a minor issue(maybe typo) in the transition of the DP state in P4 : Checking the existence of the Hamiltonian walk in $$$O(2^{n} \cdot n)$$$, since I'm writing a comment anyway let me explain with a little more detail which smol idea help us optimize it from $$$O(2^{n} \cdot n^2)$$$ to $$$O(2^{n} \cdot n)$$$ .
Idea — Since we only need a binary (yes/no) answer for each vertex $$$j$$$ in $$$mask$$$ to see whether it can reach $$$i$$$, we can use mask $$$X$$$ to store all that information instead of using $$$j$$$ (which is iterating over all $$$n$$$), this saves us extra $$$O(n)$$$.
Def. — $$$dp'[mask]~=~X$$$, $$$X$$$ is a subset of the $$$mask$$$, where the set-bits in $$$X$$$ indicate the vertices that allow for a successful Hamiltonian Walk across $$$mask$$$ which ends at the set-bit vertex.
Transition — For $$$i$$$-th bit that is set in $$$mask$$$ , we need to know whether $$$dp'[mask \oplus 2^{i}]$$$'s successful Walks can reach $$$i$$$-th vertex, for that we need to precalculate $$$M_{i}$$$, $$$M_{i} = $$$ mask made of vertices that are incident to $$$i$$$. If $$$M_{i}$$$ and $$$dp[mask \oplus i]$$$ share vertices we can extend our successful Walk towards $$$i$$$ and set $$$dp'[mask]$$$'s $$$i$$$-th bit as $$$1$$$.
Base — $$$dp'[2^{i}] = 2^{i}$$$ for every $$$i \le n$$$.
I'm not really sure but shouldn't the part were you wrote " Mi= mask made of vertices that are incident to i . If Mi and dp[mask⊕i] share vertices " shouldn't it be mask xor pow(2,i) ?