За единицу времени ширина полосы уменьшается на v1 + v2. Это значит, что она уменьшится от L до d за 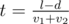 . Тот момент, когда ширина стала равна d — последний, когда Люк еще живет, значит t — это ответ.
. Тот момент, когда ширина стала равна d — последний, когда Люк еще живет, значит t — это ответ.
Отсортируем кол-ва букв по невозрастанию.
Очередную букву берем столько раз, сколько можно, но строго меньше, чем предыдущую. Не забываем, что если предыдущая буква не взята вообще, то все следующие тоже взяты не будут.
Заметим, что вершины "b" связаны со всеми остальными вершинами в графе. Найдём все подобные вершины и отметим их символом "b". После этого найдём любую непомеченную вершину V, пометим её символом "a". Все непомеченные вершины, которые связаны с V, тоже должны быть помечены символом "a". Все остальные непомеченные вершины в графе отметим символом "c".
Теперь нужно проверить корректность графа, т.е. убедиться, что все вершины "a" связаны только между собой и с вершинами "b". Аналогично проверим все вершины "c".
Хотя бы один из концов (a1 или an) изменится не больше, чем на 1. А это значит, что если gcd будет не равен 1, то он будет делиться на один из простых делителей одного из чисел a1 - 1, a1, a1 + 1, an - 1, an, an + 1. Переберём это простое.
Пусть фиксировано простое p, тогда для каждого числа мы знаем, что оно, либо уже делится на p, либо его можно поправить за b, либо оно должно входить в массив-результат.
После этого, можно запустить динамику dp[кол-во чисел, которое рассмотрели][отрезок для изменения за a еще не начался/начался/закончился] = минимальная стоимость
Итоговая сложность O(Nd) = O(NlogN), где d — количество простых делителей для перебора
Рассмотрим сперва отдельно случаи, когда все точки спроецированы на одну ось (Тогда ответ — разница между максимумом и минимумом по одной из координат)
Далее, рассмотрим самую левую и самую правую точку из тех, что спроецированы на ось x. Пусть их координаты xL и xR. Заметим, что все точки с координатами xL ≤ x ≤ xR также можно спроецировать на ось x, это не увеличит диаметр. Таким образом, если отсортировать точки по x-координате, можно считать, что точки спроецированные на ось x образуют подотрезок (непрерывный подмассив).
Запустим бинарный поиск, теперь нам нужно проверять, что можно спроецировать точки так, что диаметр <= M.
Зафиксируем самую дальнюю от 0 по x-координате точку, которая в итоге будет спроецированной на ось x. Она может быть слева или справа от нуля. Случаи будут симметричны, для примера рассмотрим случай, когда эта точка меньше 0. Пусть ее координата равна xL < 0. Заметим, что все точки, для которых 0 ≤ x - xL ≤ M и |x| ≤ |xL| можно спроецировать на ось x и от этого диаметр не увеличится, а все оставшиеся нужно спроецировать на ось y. Среди оставшихся точек нужно найти минимум и максимум по y координате и тогда ответ "можно", если расстояние между этими точками не превосходит M и расстояние от них до (xL, 0) не превосходит M.
Теперь предподсчитаем минимум и максимум y координат на префиксе и суффиксе все точек. Будем перебирать левую границу отрезка точек спроецированных на x, а правую будем искать бинпоиском или поддерживать методом двух указателей.
Таким образом одна проверка работает за O(M) или 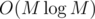 , и общая сложность
, и общая сложность 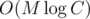 или
или 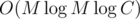 .
.
Обозначим qi = 1 - pi.
Идея решения: сначала нужно назвать каждого друга хотя бы по разу, потом на каждом шаге максимизируем вероятность закончить игру не позже, чем на данном шаге. Моделируем 300000 шагов, считая по ходу дела сумму 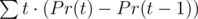 .
. 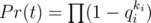 , где ki — количество раз, когда мы называли i-го друга (
, где ki — количество раз, когда мы называли i-го друга (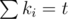 ).
).
Заметим, что матожидание с небольшой погрешностью равно 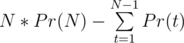 при достаточно большом N (это легко видеть, раскрыв скобки в приведенном выше выражении). Поэтому нам достаточно доказать, что
при достаточно большом N (это легко видеть, раскрыв скобки в приведенном выше выражении). Поэтому нам достаточно доказать, что
1) Приведенная выше жадная стратегия дает максимальные значения всех Pr(t).
2) На 300000 шаге погрешность меньше 10 - 6.
Доказательство:
1) Предположим, что для какого-то t набор li (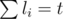 ), отличный от полученного жадным алгоритмом набора ki, дает наибольшее значение Pr(t). Возьмем какое-нибудь ka < la и kb > lb (такие найдутся, если наборы не совпадают, а их суммы равны t), тогда легко показать, что если в наборе li заменить lb на lb + 1, la на la - 1, то будет достигнуто еще большее значение Pr(t), что противоречит предположению о максимальности набора li.
), отличный от полученного жадным алгоритмом набора ki, дает наибольшее значение Pr(t). Возьмем какое-нибудь ka < la и kb > lb (такие найдутся, если наборы не совпадают, а их суммы равны t), тогда легко показать, что если в наборе li заменить lb на lb + 1, la на la - 1, то будет достигнуто еще большее значение Pr(t), что противоречит предположению о максимальности набора li.
2) Заметим, что qi ≤ 0.99. Возьмем набор ki такой, что для всех i выполняется 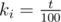 , он даст вероятность завершения игры за t шагов не большую, чем оптимальный набор. Тогда Pr(t) ≥ (1 - 0.99t / 100)100 ≥ 1 - 100·0.99t / 100. Погрешность оценки не превосходит
, он даст вероятность завершения игры за t шагов не большую, чем оптимальный набор. Тогда Pr(t) ≥ (1 - 0.99t / 100)100 ≥ 1 - 100·0.99t / 100. Погрешность оценки не превосходит 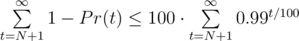 , что оценивается, как сумма геометрической прогрессии, и при N ≥ 300000 получим погрешность меньше 10 - 7.
, что оценивается, как сумма геометрической прогрессии, и при N ≥ 300000 получим погрешность меньше 10 - 7.
623E - Преобразование последовательности Для начала заметим, что если последовательность префиксных ксоров строго возрастает, то на каждом шаге ai имеет хотя бы один новый бит по сравнению с предыдущими элементами. Так как битов всего k, длина последовательности не может быть больше k. Поэтому если n > k, то ответ 0.
Решим сначала задачу за O(k3). Посчитаем dp[n][k] — количество последовательностей длины n таких, что a1|a2|... |an имеет ровно k битов. Переход — добавить l новых битов и выбрать произвольно значения k битов, которые уже вошли в префиксный ксор. Значит, dp[n + 1][k + l] должно быть увеличено на dp[n][k]·2k·Ck + ll. Биномиальный коэффициент соответствует выбору добавляемых l битов из k + l, которые будут представлены в a1|a2|... |an + 1.
Заметим, что переход не зависит от n, поэтому попробуем применить идею бинарного возведения в степень. Пусть мы хотим слить динамики dp1[k], dp2[k], где k — количество битов в a1|a2|... |aleft и b1|... |bright соответственно. Хотим посчитать dp[k] для массивов размера left + right. Формула получается такая:
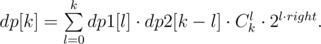
Здесь l соответствует битам в ксоре левой части, и для каждого числа из правой части эти l битов можно выбрать произвольно. Перепишем формулу так:
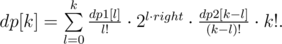
Значит, мы можем посчитать dp[k] для всех k, перемножив многочлены 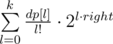 и
и 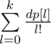 . Коэффициенты первого получаются из коэффициентов второго за
. Коэффициенты первого получаются из коэффициентов второго за 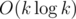 . Значит, мы можем посчитать динамику для всех длин — степеней двойки за
. Значит, мы можем посчитать динамику для всех длин — степеней двойки за 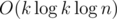 , используя быстрое преобразование Фурье. На самом деле, удобнее насчитывать
, используя быстрое преобразование Фурье. На самом деле, удобнее насчитывать 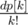 , используя то же самое равенство. Далее, используя ту же стратегию слияния, можно найти ответ для данного n, используя динамику для степеней двойки. Получили решение за
, используя то же самое равенство. Далее, используя ту же стратегию слияния, можно найти ответ для данного n, используя динамику для степеней двойки. Получили решение за 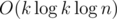 .
.
Мы решили попросить ответ по модулю 109 + 7, чтобы участники не смогли легко догадаться, что это задача на FFT :) Поэтому для получения ОК нужно было реализовать один из методов перемножения многочленов по большому модулю с использованием FFT. Другой подход состоял в применении алгоритма Карацубы, наша его реализация не укладывалась в ТЛ, однако jqdai0815 каким-то образом смог заставить свое решение с Карацубой пройти :)










Why is the editorial for 623B the same as the one for 624B??
fixed
Я думаю, моё решение не вполне правильное и вообще оно за n*81*logn работает, как мне кажется, придумайте как его отсечь, пожалуйста :)
15811678
P.S. В моём решении не используется факторизация совсем. Можно было бы опираясь на него, дать в больших ограничениях на числа.
Where is the Solution of Div2-C Graph and String ?
We can see that, we only need 3 letters.
a node with letter 'b' will must be connected to all other nodes i.e having (n-1) edges.
so for each node with (n-1) edges, assume that it's letter is 'b'.
Then for each node 'x' that is not assigned a letter yet, assume it's 'a', and for each other node 'y' that has an edge with 'x', assume it's 'a', and for each node 'y' that has no edge with 'x', assume it's 'c'.
after that, if the resulting string passes the second condition given in the problem statement, then you can print this string, otherwise print 'No'.
This is my code after the contest is done.
thank you..your solution works perfectly for me too...
Could you please explain the intuition behind this solution. I came up with the b part of the solution but could not fully solve it during contest.
We'll assign a letter to each node, A, B or C.
'B' types nodes are always connected to every other node, so we'll count for each node how many neighbors it has. We'll assign those who count N-1 neighbors the B letter (are connected to every other node). It's important to understand, just in case solution exist there are no more or less B nodes than the ones we've just marked, so every node that we have not marked must be either a 'A' node or a 'C' node.
Both 'A' and 'C' nodes can not be connected, while every A node must be connected with every other A node and every other C node must be connected with every other C node. Also both 'A' and 'C' must be connected to every 'B' node but we already know that from the first step! so we just ignore this detail that we already know. From the definition above you must note that as 'A' nodes and 'C' nodes have exactly the same definition we could easily in a correct solution change every 'A' type node to 'C' type and vice-versa (common sense guys!), so to continue with our solution we'll get any node that is not of 'B' type and we'll assign to it the letter 'A' (could be 'C' and the solution does not change). We know that all 'A' nodes are connected to each other. This means that if the correct solution exist then every node connected to the node we've just marked (except those of type B) must be'A'. So now we assign the letter 'A' to each of them. Then we'll do the same with any of the nodes not marked yet, assigning the 'C' letter to it and then to every of its neighbors.
We now can make the first control to check if the chance is correct. If there are nodes that we did not mark either 'A','B' or 'C' then the graph given is invalid
Nodes recently marked as 'B' does not determine the solution because they are connected to each other node and nothing could happen to invalidate the graph with those nodes.
So we need to check if both the 'A' nodes and the 'C' nodes follow the rules To both of those cases we'll check every node of the two groups to be connected to every node of its group and to not be connected with a node of the other group. If the first happens with every node and the second does not happen with any node, then the solution is correct and all that we need to do is to print the letter assigned to every node.
Check my solution 15811518!
I have the exact same solution for C, but I don't know why I failed during contest. I used bipartie graph. I connected all nodes that are not connected, then I check if that graph could be a bipartie graph. My code: http://codeforces.me/contest/624/submission/15799060
Sorry, I understand why I was wrong.
And that is the way editorials should be written :)
thank you :D
But there is symmetry,right? For example: If there is an answer aaabbbc,the answer cccbbba also true?
correct, there is such symmetry because the definition of A nodes is the same as the definition of C ones
b's must have edges to all other vertices -> So all index's with N-1 edges must be b's. Now, we can observe that the complement of the Graph must be bipartite. Performing coloring on that we can label each node (or index) as 'a' or 'c' and then print the resultant string.
In the end, just do another check to make sure that the string satisfies the constraints.
Code : http://codeforces.me/contest/624/submission/15810436
Не могли бы объяснить почему такое решение задачи А не прошло?
Проблемы с точностью. Питон такой питон.
Жюри округлило ответ вниз (мой -- 0.605901287553648, жюри --0.605901). Ваш ответ прошел-бы, если-бы жюри использовало больше цифр. Еще можно вместо условия на right-left использовать фиксированное количество итераций (100) чтобы избежать сюрпризов. Но Питон я думаю не виноват.
Слишком маленький эпсилон — 0.000001. Если взять 0.000000001, то проходит.
Тогда уж слишком большой.
Тогда уж слишком большой.
Альтернативное решение по C div1:
Сделаем бинпоиск по ответу. Теперь нам нужно решить 2-SAT (для каждой точки у нас есть два взаимоисключающих варианта). Стандартное решение — нужно построить разбиение на компоненты сильной связности. Для этого нам нужно уметь пускать DFS по прямым и по обратным ребрам. Заметим, что если из данной вершины есть еще прямые ребра, то есть и прямые ребра в самую далекую вершину по одному из четырех направлений. Если мы заранее отсортируем все точки по X и по Y (в двух разных массивах), то поддерживая указатели на границы не использованных вершин, мы можем сделать DFS по прямым ребрам за O(n). Чтобы сделать DFS по обратным ребрам, заметим, что каждому обратному ребру (v, u) соответствует прямое ребро (v', u') (если v и v' соответствуют парным вершинам в 2-SAT), а искать прямые ребра мы уже умеем.
В итоге получаем решение за O(n(logn + logC))
Stupid but true: I solved Div. 2 A using Binary Search :| I think you should add binary search tag to the problem haha.
Well, you can always divide using binary search
You should have done it by ternary search :)
You forgot to translate the word Разбор in the title, Sir.
Можете объяснить зачем нужен первый бинпоиск в задаче С (ну или что не так с моим решением)?
У меня зашло такое решение:
Отсортируем точки по координате x, затем переберём левую границу в порядке возрастания координат, а правую будем поддерживать методом двух указателей. Пусть левая граница — это i-я точка, тогда правая граница j — это самая ранняя точка, такая, что, если мы возьмём все точки от i до j с проекцией на ось Ox, то ответ будет равен (x[j] - x[i])2. Также проверим ответ для случая, когда мы спроецировали на Ox отрезок от i до j - 1. Теперь повторим это, двигаясь справа налево. Затем проделаем всё тоже самое, только с координатой y.
Код: 15806724.
Не очень очевидно, почему при сдвиге левой границы вправо, не может быть выгодно сдвинуть правую границу влево. (Например в решении с бинпоиском такое, определенно, иногда приходится делать)
My dfs timed out in Problem C div 2. Guess it doesn't work, or perhaps some coding error...
Don't you think that Problem D and E for div 2 are a little bit too difficult? It would be more competitive if Acceptance of D were more than 50 or so.....
Can somebody explain 623D, it's not on editorial...
I haven't proof to this solution, but it's simple and has got AC.
Iterate number of rounds (200000 is enough). Some rounds are already played, and you know probability of each friend to be right guessed (denote as g[i]). Let's guess k-th friend. Then we count probability of situation, when all friends, except k-th, are already right guessed, and now we right guess k-th friend: v[k] = g[1] * g[2] * ... * g[n] / g[k] * (1 — g[k]) * p[k] / 100. Add to answer: answer = answer + number * v[k]. It's optimally to take friend with maximum v[k].
It's enough to choose maximum v[k] in O(n) in each iteration, maintaining value g[1] * g[2] * ... * g[n].
To avoid problem with divide by g[k] = 0, at the beginning you need to try to guess each friend, then answer = (p[1] / 100) * (p[2] / 100) * ... * (p[n] / 100) * n.
Interestingly, when I raise the number of trails to 500000, it starts giving wrong answer towards author's solution (15819467), I think there're something to do with precisions of long double tho.
Edit: looks like long double brings more accurate results (15824577)
Let's say at some stage x we take some vj > vi. Note that we must eventually take vi later, or else the expected value will be infinity. So let's say we take vi at position y > x. But xvi + yvj < xvj + yvi, which means we would've done better if we had taken vi first.
I think Div2 B should be c[i ]= min(a[i], c[i - 1]-1)
Did anyone solve 624C by checking whether complement of the graph is biparite or not? Is there something wrong in this algo?
I made this mistake too. The complement has to be composed of isolated vertices and one complete bipartite graph.
b's must have edges to all other vertices -> So all index's with N-1 edges must be b's. Now, we can observe that the complement of the Graph must be bipartite. Performing coloring on that we can label each node (or index) as 'a' or 'c' and then print the resultant string. In the end, just do another check to make sure that the string satisfies the constraints. Code : http://codeforces.me/contest/624/submission/15810436
Solved 624C - Graph and String with a different approach
I checked for any unconnected edge, which implied that one end had to be 'a' and the other 'c'. So mark them as 'a' and 'c' respectively
Now for all the other nodes check their edges with the found nodes in previous step, there would be 4 possibilities:
1) Connected to both, mean the node is 'b'
2) Connected to the one marked 'a' only, mean the node is 'a'
3) Connected to the one marked 'c' only, mean the node is 'c'
4) Connected to none, means such a graph can't exist.
You now have the if and only possible string, (other possible string would just have been, if you taken the node marked 'a' as 'c' and vice versa)
Now just check for its validity
This is my code 15819935
Can somebody please explain Array GCD in more detail? The dp solution as well as the logarithmic term in complexity is not clear to me. Thanks.
I followed your method creating a dp[n][3] (haven't/started/finished), my solution got accepted but I didn't took care of the whole array being deleted. Were the test cases too weak or dp takes care of this itself, if yes how? My code is here : VastoLorde95 riadwaw
Oh, sorry got it. All elements are greater than 1 so deleting n-1 elements would ensure gcd > 1.
Problem E:
Let the exponential generating function of dpi be pi(x), so pi(x) = (ex - 1)pi - 1(2x).
The answer is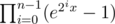 .
.
The above formula is missing a factor of ex.
In fact, multiplying this out shows that you get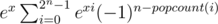 , which shows that the answer equals (the nice expression!)
, which shows that the answer equals (the nice expression!) 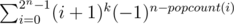 after extracting the answer. I have no idea if this leads to anything nice though.
after extracting the answer. I have no idea if this leads to anything nice though.
Please can you add editorial for div1 D ?
done
Can you improve it a little? I don't understand anything...how to choose optimal k? I really don't get it.
for the question graph and string test 24 input: 6 4 3 2 1 3 6 5 4 6 output: Yes cccaaa my output: No as there is no edge between 1 and 2 how can they both be c?
^ignore the above comment i read it wrong my bad :/
Ммм, в 623B - НОД массива очень полезный эдиториал, у меня такой же был готов минут через 20 после прочтения условия.
Как перебирать простые делители, если числа до 1e9?
Ну простые за корень перебираются, а чисел (у которых надо перебрать) всего 6
Точно, мы ведь как минимум одно из крайних обязательно возьмем. Спасибо!
Look at the full-solution explanation I made of problem E Div2 (C Div1) "Electric Charges" here :)
Could somebody explain the solution to problem Array Gcd?