I hope you enjoyed the contest! Let me know if you find any errors below. Thanks for participating.
Short solutions:
- Slime Combining: You can just do what's described in the statement. Or, maybe you can do something with the binary representation of the number.
- Guess the permutation: Find out where 1 should go. Then, find out where 2 should go, and so on.
- Constellation: Start with a triangle and break it up. Or, choose a point and look at angles. Or, sort by x coordinate.
- Hamiltonian Spanning Tree: Two cases: X > Y and X <= Y. For X > Y we can almost always avoid the spanning tree edges. For X <= Y we can do something greedy.
- Robot Arm: Make a segment tree on segments. A segment is basically just a linear transformation, which can be described with three numbers.
- Double Knapsack: Make the problem harder. Let's say I want a consecutive sublist of both lists that have equal sums. Then use pigeonhole principle to get an answer.
- Combining Slimes: Use conditional expectations. Define E[value of squares i .. n | i-th square has value j, and will not be merged with anything]. Notice that it's almost impossible for us to get a slime with value >= 50. Then, somehow generalize to large values of n (either by linear interpoloation or matrix exponentiation).
Long solutions:
Slime Combining
We can simulate the process described in the problem statement. There are many possible implementations of this, so see the example code for one possible implementation. This method can take O(n) time.
However, there is a faster method. It can be shown that the answer is simply the 1-based indices of the one bits in the binary representation of n. So, we can just do this in O(log n) time.
Example code (for simulation): http://codeforces.me/contest/618/submission/15669470
Example code (for faster method): http://codeforces.me/contest/618/submission/15669458
Guess the Permutation
One solution is to look for the column/row that contains only 1s and 0s. We know that this index must be the index for the element 1. Then, we can repeat this for 2 through n. See the example code for more details. The runtime of this solution is O(n^3).
However, there is an easier solution. One answer is to just take the max of each row, which gives us a permutation. Of course, the element n-1 will appear twice, but we can replace either occurrence with n and be done. See the other code for details
Example code (for first): http://codeforces.me/contest/618/submission/15669492
Example code (for second): http://codeforces.me/contest/618/submission/15669483
Comment: Originally, I wanted to set it so it wasn't guaranteed that there was a solution. But this seemed a bit tedious to me, so I didn't include this case.
Constellation
There are many possible solutions to this problem.
The first solution is to choose any nondegenerate triangle. Then, for each other point, if it is inside the triangle, we can replace one of our three triangle points and continue. We only need to make a single pass through the points. We need to be a bit careful about collinear points in this case.
Another solution is as follows. Let's choose an arbitrary point. Then, sort all other points by angle about this point. Then, we can just choose any two other points that have different angles, breaking ties by distance to the chosen point. (or breaking ties by two adjacent angles).
Example code (by breaking up triangles): http://codeforces.me/contest/618/submission/15669502
Example code (by angles): http://codeforces.me/contest/618/submission/15669511
Comment: Except for the second sample, all pretests didn't have collinear points. So many hacking cases are cases with collinear points.
Hamiltonian Spanning Tree
This is two separate problems: One where X > Y and when X <= Y.
Suppose X > Y. Then, we can almost always choose a path that avoides any spanning tree edges. There is one tricky case, which is the case of a star graph.
To prove the above statement, we know a tree is bipartite, so let's choose a bipartition X,Y. As long as there is exists a pair x in X and y in Y such that there isn't an edge between x and y, we can form a hamiltonian path without visiting any spanning tree edges (i.e. travel through all vertices in X and end at x, then go to y, then travel through all vertices in Y). We can see that this happens as long as it is not a complete bipartite graph, which can only happen when |X| = 1 or |Y| = 1 (which is the case of a star graph).
For the other case, X <= Y. Some intuition is that you want to maximize the number of edges that you use within the spanning tree. So, you might think along the lines of a "maximum path cover". Restating the problem is a good idea at this point.
Here's a restated version of the problem. You're given a tree. Choose the maximum number of edges such that all nodes are incident to at most 2 edges. (or equivalent a "2-matching" in this tree). Roughly, the intuition is that a 2-matching is a path cover, and vice versa.
This can be done with a tree dp, but here is a greedy solution for this problem. Root the tree arbitrarily. Then, let's perform a dfs so we process all of a node's children before processing a node. To process a node, let's count the number of "available" children. If this number is 0, then mark the node as available. If this number is 1, draw an edge from the node to its only available child and mark the node as available. Otherwise, if this number is 2 or greater, choose two arbitrary children and use those edges. Do not mark the node as available in this case.
Now, let U be the number of edges that we used from the above greedy algorithm. Then, the final answer is (n-1-U)*y + U*x).
(Proof may be added later, as mine is a bit long, unless someone has an easier proof they want to post).
Example code: http://codeforces.me/contest/618/submission/15669516
Comment: The case where X > Y and the tree is a star was not included in pretests. Thus, this could have been used to hack.
Robot Arm
We can view a segment as a linear transformation in two stages, first a rotation, then a translation.
We can describe a linear transformation with a 3x3 matrix, so for example, a rotation by theta is given by the matrix {{cos(theta), sin(theta), 0}, {-sin(theta), cos(theta), 0}, {0, 0, 1}} and a translation by L units is, {{1, 0, L}, {0, 1, 0}, {0, 0, 1}} (these can also be found by searching on google). So, we can create a segment tree on the segments, where a node in the segment tree describes the 3x3 matrix of a range of nodes. Thus updating takes O(log n) time, and getting the coordinates of the last blue point can be taken.
Some speedups. There is no need to store a 3x3 matrix. You can instead store the x,y, and angle at each node, and combine them appropriately (see code for details). Also, another simple speedup is to precompute cos/sin for all 360 degrees so we don't repeatedly call these functions.
Example code (Java): http://codeforces.me/contest/618/submission/15669521
Example code (C++): http://codeforces.me/contest/618/submission/15669530
Comment: I'm very sorry about precision issues. We realized this at the last minute, and I didn't expect so many solutions to fail because of this. I have checked my own answers against a BigDecimal implementation in Java, so try to use long doubles. Also, as a side note, this is the first ever data structure question that I've written.
Double Knapsack
Let's replace "set" with "array", and "subset" with "consecutive subarray".
Let ai denote the sum of the first i elements of A and bj be the sum of the first j elements of B. WLOG, let's assume an ≤ bn. For each ai, we can find the largest j such that bj ≤ ai. Then, the difference ai - bj will be between 0 and n - 1 inclusive. There are (n + 1) such differences (including a0 - b0), but only n integers it can take on, so by pigeon hole principle, at least two of them are the same.
So, we have ai - bj = ai' - bj'. Suppose that i' < i. It can be shown that j' < j. So, we rearranging our equation, we have ai - ai' = bj - bj', which allows us to extract the indices.
Example code: http://codeforces.me/contest/618/submission/15669546
Comment: It seemed difficult for me to generate strong cases. Is there an easy way to do it? I tried my best, but there may be some weird solutions that can pass that I just overloooked.
Combining Slimes
The probability that we form a slime with value i roughly satisfies the recurrence p(i) = p(i-1)^2, where p(1) and p(2) are given as base cases, where they are at most 999999999/1000000000. Thus, for i bigger than 50, p(i) will be extremely small (about 1e-300), so we can ignore values bigger than 50.
Let a[k][i] be the probability that a sequence of 1s and 2s can create i given that we have k squares to work with, and b[k][i] be the same thing, except we also add the constraint that the first element is a 2.
Then, we have the recurrence a[k][i] = a[k][i-1] * a[k-1][i-1], b[i][k] = b[k][i-1] * b[k-1][i-1] Note that as k gets to 50 or bigger a[k] will be approximately a[k-1] and b[k] will be approximately b[k-1] so we only need to compute this for the first 50 rows.
We can compute the probability that the square at i will have value exactly k as a[n-i][k] * (1 — a[n-i-1][k]).
Let dp[i][j] denote the expected value of the board from square i to n given that there is currently a slime with value j at index i and this slime is not going to be combined with anything else.
The final answer is just 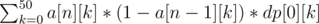
We can compute dp[i][j] using 2 cases:
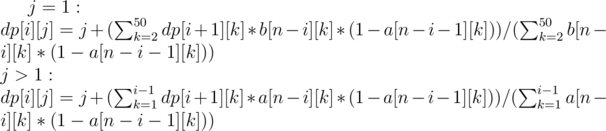
First, we compute this dp manually from n to n-50. After that, we can notice that since a[k] is equal to a[k-1] and b[k] is equal to b[k-1] for k large enough, this dp can be written as a matrix exponentiation with 50 states. Thus, this takes O(50^3 * log(n)).
Another approach that would also work is that after a large number of squares, the probabiltiy distribution of a particular square seems to converge (I'm not able to prove this though, though it seems to be true). So, by linearty of expectation, adding a square will add the same amount. So, you can do this dp up to maybe 500 or 1000, and then do linear interpolation from there.
Example code (with matrix exponentiation): http://codeforces.me/contest/618/submission/15669558
Example code (with linear interpolation): http://codeforces.me/contest/618/submission/15669560
Comments; This problem is inspired from the game 2048. The way I discovered these formulas was through some trial and error and comparing versus a bitmask dp. Try to come up with the bitmask dp solution first if you are having trouble with understanding the editorial.











I think I have an elegant O(N) solution for C for which I am pretty confident it's correct but still can't be sure before the system test. Let's take some two points, say the first two — A and B. Then if we have another two points C and D for which D is inside ABC, then S(A,B,D)<S(A,B,C). So we can simply pick the point which gives a minimum area as a third point.
UPD: Wrong answer :/
I had a similar solution to yours: First I found a line segment with no other points on, then searched for a point with least area. This solution worked for me
Oh, thank you very much! I had missed the case when there's a point inside the segment I take at the beginning... Thanks! :)
I used the same algorithm, and got the problem wrong for the same reason: I didn't think about whether the area would be 0 :(
I changed my solution to change points A and B if I found that the min area of ABC is 0 for some point C. Technically, this is O(N^3) worst case, but I implemented this and passed the system test cases.
Another solution, like what Nemmo said, would be that upon finding a point C such that the area of triangle ABC is zero: if C is on AB, use AC instead of AB and start over; otherwise, ignore it. That seems to be a lot better. It might also be possible to sort the points somehow to avoid the colinear case.
I love the problem set! The solution of F is really impressive.
I agree with you.Problem F provides an excellent constructive algorithm!
@strange_solution_for_F_that_passed_pretests 15666216
For C i sorted all points with respect to their x coordinate and then choose the first 2 point and then choose the the next possible point which is not co-linear with first 2 points.
For second problem, Guess the permutation would just finding sum of each row work? The row that has minimum sum should have 1 the second one should have 2 and so on.. It gets AC in final tests though (maybe weak test cases) but i was confused with so little constraints if this approach is right.
There should be equal amount of positive numbers in each row(because each row has same amount of zeros). So, the row with the minimum sum only consists of 0 and 1. That line will take 1.
Now, if you subtract 1 from all the positive numbers in the table, and ignore the row and columns with all zeros, the table will be about the smaller sub-problem. Also, when subtracting, the order of the row sums won't change(i. e. if row i has smaller sum than row j, it will hold true if you substract 1 from positive numbers). So, your solution works!
Lewin, here's an alternate solution to D, you can add it to editorial. Once you have the idea of path cover, note that this is equivalent to choosing a subgraph of the spanning tree such that all vertices in the subgraph have degree at most 2. This is easily done by tree dp.
Can you explained the DP solution? Thanks in advanced.
I just solved the problem using dp and posted a tutorial on my blog.
If you are interested , please read it here.Hope it will help.
I'm so happy that Egor passed his F on 1:59:34. I had 2 unsuccessful hacks on a correct submission. When I was waiting for the system testing, I saw that the current top had < 100 score advantage from me. I regretted so much because I thought I would have been the "champion" if I did not made those 2 hack. But if Egor passes his F, I would not be the champion no matter I made those 2 hacks or not. Then I don't have to regret for anything. So I kept pressing F5 for like 5 minutes until his solution has been judged. (> 100 test cases) Nearly got a heart attack. I'm still very happy because this is the first time I'm in top 5 :)
The same situation here, but I was doing that to go in top 500 and have chance for t-shirt :D After contest I realized that if I hadn't tried to hack I would be in top 400 :(
How to solve Problem A with binary Number .I have to find the non zero Positions . Then how can I find those non zero positions belongs to which numbers .
Help me please . I did it with Bruit Force approach . Thanks in Advance .
The way I approached this problem is you first convert the number to a binary string. So 9 would be 1001. I then do a for loop that would loop through each one with the variable i being my iterator.
Lets look at my example 9.
Then if I find a 1, I print out length-i. So the length (4) — i (0) to total to 4 and then again at length (4) — i (3) for a 1.
If you would like you can see it all together here: 15650979
The answer for the problem is numbers of positions of 1 in binary representation of given number: 15652379 Is there any built-in C++ function of binary logarithm? With it my code would be much more clear.
For B, I used the following logic: if the number is present at least two times in a row, then this number is the right number for the position. When there are no repetitions, put N or N-1 in any order.
Just Find out every rows Max number And store it into An Array . N-1 will Comes Twice in the List . In that Case you Can Replace anyone of those two with N .
Simulate some Test . you can Have your Result .
for problem B i just found the row having all unique values and replaced the 0 from this row with n.
It's quite convenient to use std::complex in E instead of matrices and stuff.
Thanks for this idea, it was brilliant experience for me to work with this stuff!
15740921
I wrote an O(N) solution for problem C. First we can choose two arbitrary points (I preferred two points not having the same x coordinate as it does away with the infinite slope case(Since not all points are collinear we are guaranteed to find such a pair.) ) Then we can find the point nearest to this point by using the fact that for a line y = mx+c the distance of any point(X,Y) is proportional to abs(Y-mX-c).This gives us the third point. Now as I was handling double I used an epsilon value of (1e-18) which sadly collapsed during contest. Then I used eps as (1e-6) which again failed.Finally the accepted solution uses eps as (1e-9). I think that data was such that luckily 1e-9 passes but I am not sure. Any insights into why this happens will be highly appreciated.
For problem D, is U = maximum number of edges such that all nodes are incident to at most 2 edges?
Can anyone plz help me. Why this submission fails in 16-th test? Or maybe my logic is wrong at all? Thanks.
Not, sure but you could get dist more than 8*10^18 causing undefined behavior for long long. I have the similar solution to you but failed on 85th test.
This page says that the limit for long long is greater than or equal to 2^63-1, or aproximately 9 * 10^18. So, I think it's okay to use long long.
Yeah, but particularly my solution got to 3*8*10^18. In his case it is loss of precision. Try to use eps while comparing doubles
Thank you. Problem was in the way of calculation area. There was overflow of long double
I passed problem B using backtring with proning. Is it okay I just had some luck? http://codeforces.me/contest/618/submission/15663993
In Knapsacks (F) you wrote — "Comment: It seemed difficult for me to generate strong cases. Is there an easy way to do it? I tried my best, but there may be some weird solutions that can pass that I just overloooked."
In each of two arrays there should be only a few different numbers (each of them occurring many times). And I can image the possibility that low N can be harder to solve for some programs. I think you should have given N < MAX_N - 1 in some tests. It's strange (and not right) that only samples were small.
Pretty strong special test is where only one number is repeated in one array.
Yes, I had tests like {n,n,...,n} and {n-1,...,n-1} to force big output. I also had {n-2,n-2,...,n-2,n,n} and {n-1,...,n-1} to make randomized solutions struggle. However, this case is easy to solve if you sort then try to find a common prefix or suffix sum that is the same.
I should have included some tests with small n, though it seemed my randomized solution was passing those (i.e. shuffle array using a fixed seed and store prefix sums, and if any prefix overlaps, we can just regenerate the array using the seed to reproduce output).
Basically, I tried about 4-5 different generation strategies, but it seemed random was very hard to break. My randomized solutions could pass about 90+% of tests cases in double time. Maybe there is an easier way to generate strong data.
I've seen a problem similar to problem F (Double Knapsack) before. Only there, there was a multiset of n elements between 1 and m and a multiset of m elements between 1 and n. The question is the same, and the proof is similar. Have anyone else seen a similar problem before?
Yes, it is some mathematics problem from very old russian olympiad.
but how about the others?
http://mks.mff.cuni.cz/kalva/putnam/psoln/psol934.html
can anyone explain the greedy approach for D?
I got TLE in problem D. Is my idea wrong or was it an implementation fault? I haven't found test cases where my idea fails, if it is correct i wil optimize it to get AC verdict
My Idea: If X > Y, same as editorial
If X == Y, answer is Y*(N-1)
If X < Y:
final_solution = 0
while there are unvisited vertexes:
{
find the diameter of some component of the Spanning Tree containing at least 1 unvisited vertex
mark all the vertexes in the "diameter path" as visited
final_solution += (diameter*X + Y)
remove the visited vertexes from the Spanning Tree (i don't physically remove them, just mark them so i don't insert them in another "diameter path")
}
return final_solution — Y
How are you finding the diameter?
Run BFS from any root and find the farthest vertex from this root. Now run another BFS with this farthest vertex as the root. It can be proved that the distance from the new root to the farthest vertex from the new root is the diameter of the tree.
but the edges that are out of the diameter will have y cost right? i did: printf("%lld\n",diameter*x + (n-1-diameter)*y);
and got WA.
When i find the diameter of the original Spanning Tree, i remove the vertexes in the "diameter path", and then i run the diameter algorithm again in the sub-trees induced by these vertex remotions, until there are no unvisited vertexes left. My outer loop looks like this:
for (int i = 0; i < N; i++) if (!visited[i]) total += diameter(i)*X + Y; return total - Y;This doesn't work.
For example, we can make a graph that looks like an H.
Here, the optimal solution uses the two vertical paths, which uses 8 edges. However, a solution that takes the diameter can only take 7 edges.
Wow this is a great counter-example! Thanks for the attention
Good test!
I have a little question.It's about problem C.As for the test 50,the data is (4 \n (0, 1) (0, 2) (0, 3) (7, 7)) and my answer is(1,4,2) and the outcome is that wrong output format Unexpected end of file — int32 expected.I really don't understand how can this happen or what does it mean.Can anyone help me?I have met this situation once before so I am really confused.
I found the mistake,sorry for disturbing.
For problem C, my solution was the following:
Sort the points with respect to x-coordinate (or the y-coordinate, makes no difference).
Then find the first 3 consecutive points that are not collinear.
Here is my code 15656449
after sorting find out the first 3 consecutive point that are not collinear.. why this is correct?can you please explain?
could you show us the dp version of the problem D? also 2-matching = bipartite matching?
For C , first sort all points in increasing first by x , if x coordinate equals then by y .
After sorting , for(1 to n-2)take 3 consecutive points p(i) , p(i+1) ,p(i+2) . if(area of triangle(p(i) , p(i+1) ,p(i+2))!= 0)print indexes of these 3 points.return;
There always will be a triplet of such three consecutive points.
Solution
Thank you very much!!!
Problem C editorial 'Then, for each other point, if it is inside the triangle, we can replace one of our three triangle points and continue.'
How would you find if a point is inside triangle ?
For example by counting areas. You have the triangle ABC and point P. If P is inside ABC (or on its border) than area(PAB) + area(PAC) + area(PBC) will be equal to the area of ABC, otherwise the area of ABC will be less.
I don't want to compute it via area. I'm more interested in editorial's solution:
What's going on here ?
Lol,
ccwfunction computes the cross product, which is basically an area of parallelogram with a sign that matches the direction of rotating the first vector to the second. If those cross products are non-negative than point i is in the triangle. Then you search for the pair of points from your triangle that, combined with the new point, produce a triangle with non-zero area (that way you guarantee that these three points don't lie on a line).ccw(a,b,c) returns a number > 0 if a,b,c are counterclockwise, 0 if they are collinear, or a number < 0 if a,b,c are clockwise. I first assume a,b,c are counterclockwise. Then, for any other point i, it is in the triangle if and only if {a,b,i}, {b,c,i} and {c,a,i} are all counterclockwise. After, to decide which point to replace, I make sure that the new triangle has positive area.
Thanks for interesting round and editorial.
It would be super awesome if you added images to Hamiltonian Spanning Tree explanation. I can't understand how and why the algorithm for longest path works.
problem A
how to show that? please explain!
Play 2048 and you will understand
I have exam tomorrow, can't play now. It would be better if you could explain now :)
If you have an exam tomorrow, asking questions on CF isn't what you should be doing.
why wrong answer?plz help http://www.codeforces.com/contest/618/submission/15683666
i think one of your errors is that ans in area fuction is double and it can not get a value more than 15 digits but the ranges of x and y are 10^9 and ans may have about 18 digits
What is the proof to the greedy in problem D?
А будет ли русский разбор?
I'm not so good at math,so I have many questions for problem E. Can someone help me?Thanks advance. When I was taking part in virtual contest,I found that the segment will rotate around a point instead of the origin.So I think maybe we need to record the center point and I can't "union" two nodes. Actually it can be worked simply,but I can't understand it. I can't even understand that what we should record to solve the problem.Segment,point or vector? I'm sorry about my poor English.
I had an alternative solution to B: simply take the row which has n distinct elements in it and replace the "0" with n. This works because the row which has n distinct elements is the row with the maximum element.
Problem G[problem:618G] was really awesome!! And I think there are some tiny typos in problem G's answer. For computing dp[i][j], the denominators notation should be k in sigma. Additionally, though it is brilliant idea for separating probability a and b, I think you don't need to separate those a and b if you carefully design the probability table. Anyway, thank you very much Lewin!! It was really fun to solve those problems! :)
Thanks for the catch. It seems that your submission is only using the "a" values. This seems to work because the a and b probabilities seem to be the same when you divide by the total probability. I'm not sure why that is the case, but that is an interesting observation.
Oh, I combined a and b on purpose. As you know, there are two ways to make first number 2 if the squares are more than 1. 1+1 or 2 itself. So the probability of making 2 should be p*p + (1-p) when there are squares more than two, and (1-p) if there is only one square(we cannot make 1+1 for this case) The rest processes are all same as you mentioned :)
It seems your "a" values are the same as my "a" values. Namely, a[k][2] in my code is equal to p*p + (1-p) for k >= 2 and a[1][2] = (1-p), which is the same as yours.
The interesting part I was referring to was that b[i][k]*(1-a[i-1][k]) / (sum_{j=2 to 50} b[i][j] * (1-a[i-1][j])) seems to be equal to a[i][k]*(1-a[i-1][k] / (sum_{j=2 to 50} a[i][j] * (1-a[i-1][j])) for all k between 2 and 50, and all i. The equality above is why your code works. I'm not sure why they would be equal though.
Can someone explain DP approach in problem D ?
Can somebody please explain >.<
"Comment: It seemed difficult for me to generate strong cases. Is there an easy way to do it? I tried my best, but there may be some weird solutions that can pass that I just overloooked."
Indeed, first heuristic solution that came to my mind was:
1) sort
2) check prefixes
3) reverse
4) check prefixes
5) while (1) { random_shuffle, check prefixes }
and it surprisingly passed all tests (today, not during contest :)). What is more, even after removing random it was still sufficient! However, together with Errichto we came up with testcase that makes this solution fail
n
1 ... 1 n-1 n-1 n
n ... n
But that was not an easy task to generate it :)
Doesn't the heuristic get the correct answer with n = n during step 4? I had the same heuristic so I'm also trying to find a counterexample.
Edit: just noticed that this was from 3 years ago ...
There's also a dynamic programming approach to problem D. Since the editorial doesn't explain it, I'll try to explain it here.
The beginning of the solution is virtually the same as that of the editorial: if $$$X > Y$$$, then we can always avoid all spanning tree edges UNLESS we have $$$\ge n - 1$$$ leaf nodes, in which case we have to visit one of the spanning tree edges.
The interesting part is when $$$X \le Y$$$. In this case, you can reduce this to decomposing the tree into some number of vertex-disjoint paths. We want to maximize the number of edges used. This is a great candidate for dynamic programming because it works nicely for subtrees. Namely, for each vertex, we have three cases: 0) either the vertex is never used in any path 1) the vertex is used at the end of a path 2) the vertex is used but not at the end of a path.
Transitions are also pretty straight forward.
because we can chose whatever we want from the subtrees.
We have a double summand, so it's going to be too slow if you do it naively.You can speed it up by calculating the "deltas": record the difference between $dp[i][1]$ and $$$max(dp[i][0], dp[i][1], dp[i][2])$$$ and take whichever one works best, namely the largest one.
With the second type of state (when a node is in the middle of some path), it's virtually the same idea, except we chose the best 2 nodes instead of the best node.
143571074
Footnote: It would be interesting to see if someone could get rid of one of the three states: I suspect (this is just a suspicion), that state 0 isn't really necessarily, but I could be wrong. Can anyone think of a case in which it's strategic to exclude a node?