I hope you enjoyed the contest! Let me know if you find any errors below. Thanks for participating.

Short solutions:

• Slime Combining: You can just do what's described in the statement. Or, maybe you can do something with the binary representation of the number.
• Guess the permutation: Find out where 1 should go. Then, find out where 2 should go, and so on.
• Constellation: Start with a triangle and break it up. Or, choose a point and look at angles. Or, sort by x coordinate.
• Hamiltonian Spanning Tree: Two cases: X > Y and X <= Y. For X > Y we can almost always avoid the spanning tree edges. For X <= Y we can do something greedy.
• Robot Arm: Make a segment tree on segments. A segment is basically just a linear transformation, which can be described with three numbers.
• Double Knapsack: Make the problem harder. Let's say I want a consecutive sublist of both lists that have equal sums. Then use pigeonhole principle to get an answer.
• Combining Slimes: Use conditional expectations. Define E[value of squares i .. n | i-th square has value j, and will not be merged with anything]. Notice that it's almost impossible for us to get a slime with value >= 50. Then, somehow generalize to large values of n (either by linear interpoloation or matrix exponentiation).

Long solutions:

Slime Combining

We can simulate the process described in the problem statement. There are many possible implementations of this, so see the example code for one possible implementation. This method can take O(n) time.

However, there is a faster method. It can be shown that the answer is simply the 1-based indices of the one bits in the binary representation of n. So, we can just do this in O(log n) time.

Example code (for simulation): http://codeforces.me/contest/618/submission/15669470

Example code (for faster method): http://codeforces.me/contest/618/submission/15669458

Guess the Permutation

One solution is to look for the column/row that contains only 1s and 0s. We know that this index must be the index for the element 1. Then, we can repeat this for 2 through n. See the example code for more details. The runtime of this solution is O(n^3).

However, there is an easier solution. One answer is to just take the max of each row, which gives us a permutation. Of course, the element n-1 will appear twice, but we can replace either occurrence with n and be done. See the other code for details

Example code (for first): http://codeforces.me/contest/618/submission/15669492

Example code (for second): http://codeforces.me/contest/618/submission/15669483

Comment: Originally, I wanted to set it so it wasn't guaranteed that there was a solution. But this seemed a bit tedious to me, so I didn't include this case.

Constellation

There are many possible solutions to this problem.

The first solution is to choose any nondegenerate triangle. Then, for each other point, if it is inside the triangle, we can replace one of our three triangle points and continue. We only need to make a single pass through the points. We need to be a bit careful about collinear points in this case.

Another solution is as follows. Let's choose an arbitrary point. Then, sort all other points by angle about this point. Then, we can just choose any two other points that have different angles, breaking ties by distance to the chosen point. (or breaking ties by two adjacent angles).

Example code (by breaking up triangles): http://codeforces.me/contest/618/submission/15669502

Example code (by angles): http://codeforces.me/contest/618/submission/15669511

Comment: Except for the second sample, all pretests didn't have collinear points. So many hacking cases are cases with collinear points.

Hamiltonian Spanning Tree

This is two separate problems: One where X > Y and when X <= Y.

Suppose X > Y. Then, we can almost always choose a path that avoides any spanning tree edges. There is one tricky case, which is the case of a star graph.

To prove the above statement, we know a tree is bipartite, so let's choose a bipartition X,Y. As long as there is exists a pair x in X and y in Y such that there isn't an edge between x and y, we can form a hamiltonian path without visiting any spanning tree edges (i.e. travel through all vertices in X and end at x, then go to y, then travel through all vertices in Y). We can see that this happens as long as it is not a complete bipartite graph, which can only happen when |X| = 1 or |Y| = 1 (which is the case of a star graph).

For the other case, X <= Y. Some intuition is that you want to maximize the number of edges that you use within the spanning tree. So, you might think along the lines of a "maximum path cover". Restating the problem is a good idea at this point.

Here's a restated version of the problem. You're given a tree. Choose the maximum number of edges such that all nodes are incident to at most 2 edges. (or equivalent a "2-matching" in this tree). Roughly, the intuition is that a 2-matching is a path cover, and vice versa.

This can be done with a tree dp, but here is a greedy solution for this problem. Root the tree arbitrarily. Then, let's perform a dfs so we process all of a node's children before processing a node. To process a node, let's count the number of "available" children. If this number is 0, then mark the node as available. If this number is 1, draw an edge from the node to its only available child and mark the node as available. Otherwise, if this number is 2 or greater, choose two arbitrary children and use those edges. Do not mark the node as available in this case.

Now, let U be the number of edges that we used from the above greedy algorithm. Then, the final answer is (n-1-U)*y + U*x).

(Proof may be added later, as mine is a bit long, unless someone has an easier proof they want to post).

Example code: http://codeforces.me/contest/618/submission/15669516

Comment: The case where X > Y and the tree is a star was not included in pretests. Thus, this could have been used to hack.

Robot Arm

We can view a segment as a linear transformation in two stages, first a rotation, then a translation.

We can describe a linear transformation with a 3x3 matrix, so for example, a rotation by theta is given by the matrix {{cos(theta), sin(theta), 0}, {-sin(theta), cos(theta), 0}, {0, 0, 1}} and a translation by L units is, {{1, 0, L}, {0, 1, 0}, {0, 0, 1}} (these can also be found by searching on google). So, we can create a segment tree on the segments, where a node in the segment tree describes the 3x3 matrix of a range of nodes. Thus updating takes O(log n) time, and getting the coordinates of the last blue point can be taken.

Some speedups. There is no need to store a 3x3 matrix. You can instead store the x,y, and angle at each node, and combine them appropriately (see code for details). Also, another simple speedup is to precompute cos/sin for all 360 degrees so we don't repeatedly call these functions.

Example code (Java): http://codeforces.me/contest/618/submission/15669521

Example code (C++): http://codeforces.me/contest/618/submission/15669530

Comment: I'm very sorry about precision issues. We realized this at the last minute, and I didn't expect so many solutions to fail because of this. I have checked my own answers against a BigDecimal implementation in Java, so try to use long doubles. Also, as a side note, this is the first ever data structure question that I've written.

Double Knapsack

Let's replace "set" with "array", and "subset" with "consecutive subarray".

Let a_i denote the sum of the first i elements of A and b_j be the sum of the first j elements of B. WLOG, let's assume a_n ≤ b_n. For each a_i, we can find the largest j such that b_j ≤ a_i. Then, the difference a_i - b_j will be between 0 and n - 1 inclusive. There are (n + 1) such differences (including a₀ - b₀), but only n integers it can take on, so by pigeon hole principle, at least two of them are the same.

So, we have a_i - b_j = a_i' - b_j'. Suppose that i' < i. It can be shown that j' < j. So, we rearranging our equation, we have a_i - a_i' = b_j - b_j', which allows us to extract the indices.

Example code: http://codeforces.me/contest/618/submission/15669546

Comment: It seemed difficult for me to generate strong cases. Is there an easy way to do it? I tried my best, but there may be some weird solutions that can pass that I just overloooked.

Combining Slimes

The probability that we form a slime with value i roughly satisfies the recurrence p(i) = p(i-1)^2, where p(1) and p(2) are given as base cases, where they are at most 999999999/1000000000. Thus, for i bigger than 50, p(i) will be extremely small (about 1e-300), so we can ignore values bigger than 50.

Let a[k][i] be the probability that a sequence of 1s and 2s can create i given that we have k squares to work with, and b[k][i] be the same thing, except we also add the constraint that the first element is a 2.

Then, we have the recurrence a[k][i] = a[k][i-1] * a[k-1][i-1], b[i][k] = b[k][i-1] * b[k-1][i-1] Note that as k gets to 50 or bigger a[k] will be approximately a[k-1] and b[k] will be approximately b[k-1] so we only need to compute this for the first 50 rows.

We can compute the probability that the square at i will have value exactly k as a[n-i][k] * (1 — a[n-i-1][k]).

Let dp[i][j] denote the expected value of the board from square i to n given that there is currently a slime with value j at index i and this slime is not going to be combined with anything else.

The final answer is just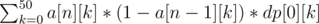

We can compute dp[i][j] using 2 cases:

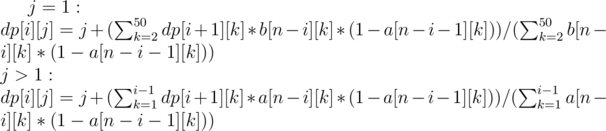
First, we compute this dp manually from n to n-50. After that, we can notice that since a[k] is equal to a[k-1] and b[k] is equal to b[k-1] for k large enough, this dp can be written as a matrix exponentiation with 50 states. Thus, this takes O(50^3 * log(n)).

Another approach that would also work is that after a large number of squares, the probabiltiy distribution of a particular square seems to converge (I'm not able to prove this though, though it seems to be true). So, by linearty of expectation, adding a square will add the same amount. So, you can do this dp up to maybe 500 or 1000, and then do linear interpolation from there.

Example code (with matrix exponentiation): http://codeforces.me/contest/618/submission/15669558

Example code (with linear interpolation): http://codeforces.me/contest/618/submission/15669560

Comments; This problem is inspired from the game 2048. The way I discovered these formulas was through some trial and error and comparing versus a bitmask dp. Try to come up with the bitmask dp solution first if you are having trouble with understanding the editorial.