Этот раунд был немного необычным: некоторые из задач были ранее подготовлены студентами и сотрудниками Саратовского ГУ для прошедших олимпиад, одна из задач была подготовлена участником dalex для одного из регулярных (неучебных) раундов Codeforces, но не использована там.
Отсортируем массив по невозрастанию. Тогда ответом на задачу будет несколько первых флешек. Будем идти по массиву слева направо пока не наберем сумму m. Количество взятых элементов и будет ответом на задачу.
Асимптотическая сложность решения: O(nlogn).
Пусть cnti — количество книг i-го жанра. Тогда ответом на задачу будет величина равная 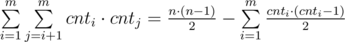 . В первой сумме мы считаем непосредственно количество хороших пар книг, а во втором из общего количества пар книг вычитаем количество плохих пар.
. В первой сумме мы считаем непосредственно количество хороших пар книг, а во втором из общего количества пар книг вычитаем количество плохих пар.
Асимптотическая сложность решения: O(n + m2) или O(n + m).
Пусть s — сумма элементов массива. Если число s делится на n, то сбалансированный массив будет состоять из n чисел  . В этом случае разность между минимальным и максимальным будет равна 0. Легко видеть, что в любом другом случае ответ будет больше 0. С другой стороны массив, состоящий из
. В этом случае разность между минимальным и максимальным будет равна 0. Легко видеть, что в любом другом случае ответ будет больше 0. С другой стороны массив, состоящий из 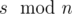 чисел
чисел 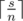 и
и 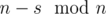 чисел
чисел 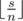 является сбалансированным с разницей минимального и максимального равной 1. Обозначим этот сбалансированный массив b. Чтобы получить массив b давайте сначала отсортируем массив a по невозрастанию, а после этого попарно сопоставим элементы массивов a, b друг другу. Таким образом некоторые числа в a придется увеличить до соответствующих чисел в b, а некоторые уменьшить. Поскольку за одну операцию мы сразу уменьшаем где-то значение, а где-то увеличиваем, то ответ равен
является сбалансированным с разницей минимального и максимального равной 1. Обозначим этот сбалансированный массив b. Чтобы получить массив b давайте сначала отсортируем массив a по невозрастанию, а после этого попарно сопоставим элементы массивов a, b друг другу. Таким образом некоторые числа в a придется увеличить до соответствующих чисел в b, а некоторые уменьшить. Поскольку за одну операцию мы сразу уменьшаем где-то значение, а где-то увеличиваем, то ответ равен 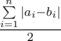 .
.
Асимптотическая сложность решения: O(nlogn).
609D - Gadgets for dollars and pounds
Заметим, что если Нура может купить k гаджетов за x дней то за x + 1 день она тоже сможет их купить. Таким образом, функция возможности покупки является монотонной. Значит, мы можем найти минимальный день с помощью бинарного поиска. Пусть lf = 0 — левая граница бинарного поиска, а rg = n + 1 — правая. Будем поддерживать инвариант, что в левой границе мы не можем купить k гаджетов, а в правой можем (будем считать, что в n + 1 день мы гаджеты стоят 0). Теперь зафиксируем некоторый день d и поймем можем ли мы купить k гаджетов за d дней. Введем функцию f(d), которая равна 1, если мы можем купить k гаджетов за d дней и 0 в противном случае. Каждый раз в качестве d будем выбирать значение 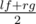 . Если f(d) = 1, то нужно двигать правую границу бинарного поиска rg = d, иначе левую lf = d. По завершении бинарного поиска нужно проверить если lf = n + 1, то ответ - 1, иначе ответ равен lf. Для вычисления функции f(d) предварительно образуем 2 массива стоимостей гаджетов, продающихся за доллары и фунты, и отсортируем их. Теперь заметим, что мы можем покупать гаджеты за доллары в день i ≤ d когда доллар стоит меньше всего и день j ≤ d, когда фунт стоит меньше всего. Пусть теперь мы хотим купить x гаджетов за доллары и соответственно k - x за фунты. Конечно мы будем покупать самые дешевые из них (для этого мы и отсортировали заранее массивы). Будем перебирать x от 0 до k и одновременно поддерживать сумму стоимостей долларовых гаджетов s1 и фунтовых s2. Для x = 0 эту сумму легко посчитать за O(k), для всех остальных x эту сумму можно пересчитать за O(1) из суммы для x - 1 добавлением очередного долларового гаджета и выкидываением фунтового.
. Если f(d) = 1, то нужно двигать правую границу бинарного поиска rg = d, иначе левую lf = d. По завершении бинарного поиска нужно проверить если lf = n + 1, то ответ - 1, иначе ответ равен lf. Для вычисления функции f(d) предварительно образуем 2 массива стоимостей гаджетов, продающихся за доллары и фунты, и отсортируем их. Теперь заметим, что мы можем покупать гаджеты за доллары в день i ≤ d когда доллар стоит меньше всего и день j ≤ d, когда фунт стоит меньше всего. Пусть теперь мы хотим купить x гаджетов за доллары и соответственно k - x за фунты. Конечно мы будем покупать самые дешевые из них (для этого мы и отсортировали заранее массивы). Будем перебирать x от 0 до k и одновременно поддерживать сумму стоимостей долларовых гаджетов s1 и фунтовых s2. Для x = 0 эту сумму легко посчитать за O(k), для всех остальных x эту сумму можно пересчитать за O(1) из суммы для x - 1 добавлением очередного долларового гаджета и выкидываением фунтового.
Асимптотическая сложность решения: O(klogn).
609E - Minimum spanning tree for each edge
Задача была предложена участником dalex.
Эта задача является очень стандартной задачей на знание минимальных покрывающих деревьев и умение построить некоторую структуру данных на дереве, для вычисления некоторой функции. Построим любое минимальное покрывающее дерево любым быстрым алгоритмом (например алгоритмом Краскала). Для всех ребер вошедших в MST мы уже нашли ответ — это просто вес MST. Теперь рассмотрим любое другое ребро (x, y). В MST существует единственный простой путь от вершины x к вершине y. Найдем на этом пути самое длинное ребро, выкинем его и добавим ребро (x, y). Согласно критерию Тарьяна, получившееся дерево является минимальным покрывающим, содержащим ребро (x, y) (это не является утверждением критерия Тарьяна, но из него следует).
Теперь рассмотрим техническую сторону решения. Для того, чтобы быстро находить самое длинное ребро на пути между двумя вершинами в дереве подвесим дерево за любую вершину (например за первую). Теперь обозначим l = lca(x, y) — наименьший общий предок вершин (x, y). lca(x, y) можно искать с помощью метода двоичного подъема, одновременно поддерживая самое тяжелое ребро.
Конечно такую задачу можно решать и более сложными структурами данных, например с помощью Heavy-light decomposition или Linkcut tree.
Асимптотическая сложность решения: O(mlogn).
В этой задаче нужно было реализовать все, что написано в условии, но за хорошую асимпотику. Будем поддерживать множество пока не съеденных комаров (например с помощью set} в C++ или TreeSet в Java) и обрабатывать приземления комаров по очереди. Также будем поддерживать множество отрезков (ai, bi), где ai — положение i-й лягушки, а bi = ai + li, где li — длина языка i-й лягушки. Пусть очередной комар приземлился в точке x. Выберем среди отрезков (ai, bi) отрезок с минимальным ai таким, что bi ≥ x. Если окажется, что ai ≤ x, то этот отрезок и будет соответствовать лягушке, которая съест комара. Иначе комара никто не съест и его нужно добавить в множество несъеденных. Если комара съест i-я лягушка, то нужно удлинить её язык на размер комара и обновить отрезок (ai, bi) в структуре данных. После этого нужно в множестве несъеденных комаров брать ближайшего к лягушке справа и если возможно есть этого комара (это можно сделать с помощью например метода lower_bound в C++). Возможно лягушка сможет съесть несколько комаров, в этом случае их нужно по очереди есть.
Отрезки (ai, bi) можно хранить например в динамическом дереве отрезков по правому концу bi, а значениями хранить ai. Либо то же самое можно делать с помощью декартова дерева. Но это слишком сложно можно написать более простое решение. Будем хранить в обычном дереве отрезков для каждого левого конца ai (левые концы не меняются никогда) правый конец bi. Теперь можно например бинарным поиском найти минимальный префикс максимум на котором больше либо равен x. В этом случае получаем решение за O(nlog2n). Но это решение можно улучшить. Для этого нужно просто спускаться по дереву отрезков: если в левой половине максимум больше либо равен x идем влево иначе вправо.
Асимптотическая сложность решения: O((n + m)log(n + m)).











I hope you liked my problem E. I'll also try to add some new tests tomorrow, if I have time.
This is the comment with its solution: http://codeforces.me/blog/entry/9570#comment-150780.
Was just a lot of copy-pasting for me :)
This E is really nice.
Any hint on solving with Heavy-light decomposition method or Link Cut Trees? Thanks.
My solution :) http://codeforces.me/contest/609/submission/14893860 Sorry for the chinese comment...
In case someone will be interested, recently I posted even shorter HLD implementation: http://codeforces.me/blog/entry/22072
Thanks DaiDaiBear Al.Cash !
В задаче C сортировка абсолютно не нужна. Пусть av — среднее с округлением вверх, а k — количество чисел больше av. ans= сумма (a[i]-av)*(av>a[i]) + (k > sum%n && sum%n!=0) ? k — sum%n : 0.
TODO)
Видимо, вместо этого нужно добавить, что осталось попробовать той же лягушкой съесть ещё комаров.
Кроме этого я еще допишу, как это проще написать (без декартовых деревьев, динамических деревьев отрезков и прочего).
UPD: Готово.
В общем-то дерево отрезков излишне, можно обойтись стандартными упорядоченными сетами и мепами с операциями взятия первого элемента больше/меньше некоторого (lower_bound/upper_bound для C++, tailSet.first/headSet.last для Java).
Да я видел такое решение.
Problem C. For those who don't like formulae: let
cnt[i]denote number of servers with load i. Then, thanks to low numbers, there's solution that (almost) faithfully models rebalancing:How could the approach to "USB Flash Drives" be true?
Take this case for example:
a = {6,3,4,2,5}
m = 10
I presume you'll choose {2,3,4} and return 3 when you should actually choose {4,6} and return 2.
Or am I missing something?
Sort the array in non increasing order i.e. decreasing order. So the array will become : 6,5,4,3,2. You will chose 6 and 5(Till the point your sum is at least m).
What about a O(N) and a easier solution for C?? My solution: 14895448
Is my solution hack-able?
What about a O(N) and easier solution for problem C? take a look at this: 14895448
Is this solution hack-able?
I have a similar solution. There is no reason to sort the array — when we know the average, it's clear that maximum of required increments/decrements will satisfy the other one and thus it's correct (on the other hand, at least this number must be reasigned).
why are you checking this — "if(sum>(mx*n))mx++;" if you simply just assign mx=mn+1 , it will work fine .
yeah :D . it will.... it was because of my initial implementation where i just calculated sumOf(min(abs(mn-a[i]),abs(a[i]-mx)))/2; which is clearly a wrong solution!!!
i didnt knew where the upvoting tick was.. by mistake i clicked on the downvote one. now i cant change it . i am sorry ! :p
Go to his profile. Click on comments. Upvote any other 2 comments :P
В F можно обойтись без деревьев отрезков для поддержания зоны поражения лягушек: храним (a,b) в set/map с предикатом по левому концу. Попадание комара проверяем upper_bound-ом. Если лягушка (a,b) ест комара, то меняем отрезок на (a,b+d), а лягушкам, находящимся справа и попашим в (b..d) уменьшаем зону поражения, удаляя их при необходимости. Т.е. поддерживаем инвариант непересечения зон поражений.
14899153
Да круто. Руки пошли писать решение раньше, чем стоило.
For problem F, I implemented a square-root decomposition algorithm 14900791 but it gets WA on test 5. Does anybody have any idea why it fails? The general algorithm is: sort frogs by start position (increasing order), partition the frogs into size squareroot(n) sections and keep track of the maximum reach of any frog in that section, and when a mosquito lands, iterate through each section until we find that some frog can reach greater or equal to the position of the mosquito and then find the frog which works (this might not always be possible), if the frog is able to eat it then make it eat it, update the section and then try to find any un-eaten mosquitoes for this frog to eat and keep doing this until no more mosquitoes can be eaten, otherwise if the frog was not able to eat the mosquito that just landed then add it to the un-eaten mosquitoes set.
Change set to multiset.
Oh yes, mosquitoes can land at similar positions... thanks for that. Can't believe I spent an hour staring at my code without seeing that!
"To find l we can use binary lifting method. During calculation of l we also can maintain the weight of the heaviest edge" Can someone help me with how to calculate heaviest edge along with calculating lca? code...? and also can someone explain how this can also be solved using dsu? thanks in advance :)
In C how do we know that 2 divides the sum of the differences?
For every operation (moving task from one server to another) there is server where the task is moved onto (gets +1) and one where is moved from (gets -1). Since we are taking absolute value every time, both times we will increase sum by 1. So every operation adds 2 to the sum. Therefore sum is divisible by 2.
Consider the smallest example possible:
2
1 3
Average is (1 + 3) / 2 = 2. One task will be moved from server 2 (gets -1) to server 1 (gets + 1). And for this task you add abs(1 — 2) + abs(3 — 2) = 2 to the total sum.
i am not able to understand the explanation for problem C . can someone help me?
There's also an alternative solution for problem E. Consider the standard Kruskal's algorithm for finding the MST of a graph. Observe that the heaviest edge on the path from x to y in the resulting tree will be the first edge that connects the components containing x and y during the algorithm. Now while adding an edge to the current tree, simply iterate over the nodes from the smaller component and check if their neighbors are in the larger component, and merge the two components afterwards. We can use the standard disjoint set data structure for that purpose, with additionally storing all nodes from each component on a separate vector.
Pretty well solution!!!!
Quite an elegant solution!
This is my code for E. It passed 10 first cases, but time exceeds limit at test case 11. What should i change?
include <bits/stdc++.h>
using namespace std; typedef long long ll; ll n,m; ll u,v,w; ll per[200000+5];
struct p{ ll u; ll v; ll w; ll id; } e[200000+5];
bool cmp(p a,p b){ return a.w<b.w; }
ll find(ll x){ return per[x] == x ? x:find(per[x]); } int main(){ cin>>n>>m; for(int i = 0;i<m;i++){ cin>>u>>v>>w; e[i].u =u; e[i].v = v; e[i].w =w; e[i].id = i; }
}
Your solution very slow, this is O(n * m) time. You need to use fast data structures. My solution with Sparse Table on tree, DSU, MST, in O(n log(n)) time
Can you help me with how to calculate maximum edge weight along a path using sparse table. I know how to get LCA using sparse table. I read your code, couldn't figure out properly.
Update: Got it! Thanks!
98388177
Someone please help with why this code doesn't work. The test values are large so I cannot debug. Please help. Thanks!
Is it Cheriton-Tarjan Algorithm?
https://books.google.co.uk/books?id=zxSmHAoMiRUC&pg=PA78&lpg=PA78&dq=cheriton-tarjan+algorithm&source=bl&ots=LQWYqzK7bq&sig=mmKjYZ7pevW3vkPD1Xmg7GC5BOI&hl=en&sa=X&ei=0AX4UsykO_Cp7AbWiICADg#v=onepage&q=cheriton-tarjan%20algorithm&f=false
Problem F can be solved with a set instead of a segment tree. Since we are finding a segment $$$(a_i,b_i)$$$ containing $$$x$$$ with the minimal value of $$$a_i$$$, we can remove all segments which are fully contained in some other segment. Thus, sorting remaining segments by $$$a_i$$$ is the same as sorting them by $$$b_i$$$, so we can keep them in a set keyed by $$$b_i$$$, removing segments if necessary.