Lets say I have a Big Integer A and an integer B . I want to calculate A mod B in O(number_of_digits_in(A)) complexity.
How can I do that?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | adamant | 152 |
| 6 | djm03178 | 152 |
| 8 | Qingyu | 151 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
Lets say I have a Big Integer A and an integer B . I want to calculate A mod B in O(number_of_digits_in(A)) complexity.
How can I do that?
| Name |
|---|



Modular arithmetic is a great help here.
Let's say that A = 10k - 1·ak - 1 + 10k - 2·ak - 2 + ... + 100·a0, where ai are digits of A. You have to calculate that expression modulo B. Note that you can easily calculate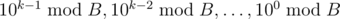 in linear time: just start with 100 = 1 and then multiply by ten (and apply modulo afterwards) until you have all k values. Now the expression is slightly simpler: you only have small numbers, so you can just calculate it straightforwardly, applying modulo after each operation.
in linear time: just start with 100 = 1 and then multiply by ten (and apply modulo afterwards) until you have all k values. Now the expression is slightly simpler: you only have small numbers, so you can just calculate it straightforwardly, applying modulo after each operation.
Another approach: A = a0 + 10·(a2 + 10·(... + 10·(ak - 1)...)). You start calculating that expression from inside: ak - 1, then you multiply it by ten and add ak - 2, and so on until a0.