Hello everyone,
Problem statement:
We have n > 2 pairs: < line, side > , side 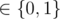 . How can we check fast if they make non-empty polygon (or point)?
. How can we check fast if they make non-empty polygon (or point)?
Cheers
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Hello everyone,
Problem statement:
We have n > 2 pairs: < line, side > , side 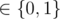 . How can we check fast if they make non-empty polygon (or point)?
. How can we check fast if they make non-empty polygon (or point)?
Cheers
| Название |
|---|



It looks like application of simplex algorithm
One approach is to sort lines by angle and then build convex hull by maintaiing stack.It might be tricky to correctly handle the case where resulting shape is single point.
This is a well-studied problem in computational geometry, known as "Half-plane intersection".
https://web.stanford.edu/class/cs97si/09-computational-geometry.pdf
code for O(n^3) : http://ideone.com/8t36e9
I would really appreciate for any help in O(nlgn) algorithm.