Простая задача на реализацию. Проитерируемся по i от 1 до n, а внутри проитерируемся по j от 1 до 2·m, причем на каждой итерации будем увеличивать j на два. Если на текущей итерации a[i][j] = '1' или a[i][j + 1] = '1' увеличим ответ на один.
Асимптотика решения — O(nm).
Будем считать ответ для каждого блока отдельно и умножать ответ для предыдущих блоков на ответ для текущего блока, при этом не забывая брать результат перемножения по модулю.
Для блока длины k ответ считается следующим образом. Пусть для этого блока число должно делиться на x и не должно начинаться с цифры y. Тогда ответ для этого блока — количество чисел из k цифр, делящихся на x, минус количество чисел, начинающихся с цифры y и состоящих из k цифр, плюс количество чисел, начинающихся с цифры y - 1 (только если y > 0) и состоящих из k цифр.
Асимптотика решения — O(n / k).
Отсортируем все точки по возрастанию координаты x, далее будем работать с перенумерованными точками.
Предположим, что при оптимальной игре после ходов игроков остались точки с номерами l и r (l < r). Утверждается, что первый игрок не запретил ни одну из точек с индексом l < i < r, ведь в противном случае он играл не оптимально и мог запретить точку l или точку r (можно показать, что это не зависит от оптимальных действий второго игрока), поменяв оптимальный ответ. Получается, что номера всех 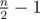 запрещенных первым игроком точек лежат вне отрезка [l, r], а значит
запрещенных первым игроком точек лежат вне отрезка [l, r], а значит 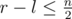 . Заметим, что выбрав некоторую такую границу [l, r] при
. Заметим, что выбрав некоторую такую границу [l, r] при 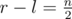 , первый игрок может всегда добиться того, чтобы точки в ответе лежали внутри этого отрезка.
, первый игрок может всегда добиться того, чтобы точки в ответе лежали внутри этого отрезка.
Второй игрок хочет добиться того, чтобы 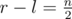 (меньше он сделать не может), то есть всегда запрещать точку, лежащую строго внутри [l, r]. Поскольку второй игрок не знает наперед, к каким точкам стремится игрок, после каждого хода первого игрока ему необходимо запрещать точку, которая лежит строго внутри каждой из возможных границ, образованных этими точками. Нетрудно показать, что эта точка является медианой оставшегося множества точек (а их нечетное количество), ведь количество оставшихся ходов первого игрока на единицу меньше количества ходов второго, и он сможет впоследствии запретить все, кроме трех медианных точек. Две крайние из них второму игроку запрещать нельзя, так как они могут впоследствии увеличить количество удаленных слева (или справа) первым игроком точек, а средняя из них как раз принадлежит всевозможным границам, которые мог выбрать первый игрок. Таким образом второй игрок всегда может свести ситуацию к
(меньше он сделать не может), то есть всегда запрещать точку, лежащую строго внутри [l, r]. Поскольку второй игрок не знает наперед, к каким точкам стремится игрок, после каждого хода первого игрока ему необходимо запрещать точку, которая лежит строго внутри каждой из возможных границ, образованных этими точками. Нетрудно показать, что эта точка является медианой оставшегося множества точек (а их нечетное количество), ведь количество оставшихся ходов первого игрока на единицу меньше количества ходов второго, и он сможет впоследствии запретить все, кроме трех медианных точек. Две крайние из них второму игроку запрещать нельзя, так как они могут впоследствии увеличить количество удаленных слева (или справа) первым игроком точек, а средняя из них как раз принадлежит всевозможным границам, которые мог выбрать первый игрок. Таким образом второй игрок всегда может свести ситуацию к 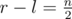 .
.
Ответ на задачу — минимум среди значений 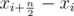 .
.
Главное утверждение для решения этой задачи — в середине дистанции каждого соревнования датчик должен находиться либо в самой верхней точке колеса, либо в самой нижней точке колеса.
Для того, чтобы посчитать ответ, воспользуемся бинпоиском. Если центр колеса прошел расстояние c то датчик переместился на расстояние c + rsin(c / r), если в середине датчик находился сверху колеса, или на расстояние c - rsin(c / r), если в середине датчие находился снизу колеса, где r — это радиус колеса.
Асимптотика решения —  .
.
Найдем центры прямоугольников и умножим их координаты на два, чтобы далее работать с целыми координатами. Тогда подходящим холодильником (для всех точек) является прямоугольник, содержащий все точки, но с длинами сторон, округленными вверх к ближайшему четному числу.
Представим теперь, что удаляем магниты с холодильника последовательно, постепенно "уменьшая" прямоугольник. Очевидно, что каждый раз выгодно удалять только те точки, что лежат на какой-то из четырех сторон прямоугольника. Переберем 4k вариантов того, как мы будем это делать, с помощью рекурсии, каждый раз удаляя одну из еще не удаленных точек с максимальным или минимальным значением по одной из координат. Если мы будем поддерживать 4 массива (или два массива в виде дека), то это можно делать за O(1) амортизированно. Такое решение будет работать за O(4k).
Можно также заметить, что описанный выше алгоритм удаляет всегда несколько самых правых, левых, верхних, и нижних точек. Можно перебрать, как k распределится среди этих величин и промоделировать удаление с помощью, например, описанных выше 4 массивов. Такое решение имеет асимптотику O(k4).
Для подсчета ответа на каждый запрос будем пользоваться формулой 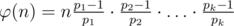 , где p1, p2, ..., pk — все простые, делящие n. Эту формулу каждый может попробовать доказать или воспользоваться уже существующими доказательствами. Все вычисления ниже производим по модулю 109 + 7
, где p1, p2, ..., pk — все простые, делящие n. Эту формулу каждый может попробовать доказать или воспользоваться уже существующими доказательствами. Все вычисления ниже производим по модулю 109 + 7
Предположим теперь, что мы решаем задачу для фиксированного левого конца отрезка l, отбросив все элементы левее. Любой запрос теперь превращается в запрос на префиксе массива. Тогда, судя по формуле, для каждого простого p нас интересует лишь его самое левое вхождение, потому что все остальные вхождения не будут влиять на правую часть в приведенной выше формуле. Превратим наш запрос на значение функции Эйлера в запрос произведения на префиксе: сначала проинициализируем дерево Фенвика произведений единицами, затем сделаем умножения в точках l, l + 1, ..., n значениями соответствующих элементов al, al + 1, ..., an, затем для каждого самого левого вхождения простого p в позицию i сделаем умножение в точке i на значение 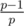 . Нетрудно убедиться, что теперь запрос на префиксе определенной длины даст правильный ответ для отрезка той же длины с левым концом в l. Такую подготовку для фиксированного левого конца можно осуществить за
. Нетрудно убедиться, что теперь запрос на префиксе определенной длины даст правильный ответ для отрезка той же длины с левым концом в l. Такую подготовку для фиксированного левого конца можно осуществить за 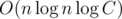 , где C — максимальное значение элемента (этот логарифм соответствует количеству простых в разложении какого-то из ai).
, где C — максимальное значение элемента (этот логарифм соответствует количеству простых в разложении какого-то из ai).
Нас интересуют все левые концы, поэтому научимся переходить от одного из них к другому. В самом деле, пусть все было посчитано для левого конца l и мы хотим теперь перейти к левому концу l + 1. Нас перестает интересовать al внутри левой части формулы, поэтому сделаем умножение в дереве Фенвика в точке l на значение al - 1. Так же нас перестают интересовать все простые внутри al (а они, очевидно, самые левые среди своих вхождений), поэтому сделаем так же умножения в точке l на все значения 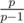 . Однако у каждого из этих простых могли существовать другие вхождения, которые теперь станут самыми левыми. Добавим их с помощью умножений, описанных выше. С помощью сортировок (или векторов) переход между соседними левыми концами реализуется за суммарную
. Однако у каждого из этих простых могли существовать другие вхождения, которые теперь станут самыми левыми. Добавим их с помощью умножений, описанных выше. С помощью сортировок (или векторов) переход между соседними левыми концами реализуется за суммарную 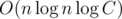 .
.
Чтобы правильно отвечать на запросы, их так же нужно правильно отсортировать (или поместить в динамический массив), и ответ на запрос будет совершать  операций. Суммарная асимптотика всего решения
операций. Суммарная асимптотика всего решения 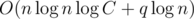 операций и
операций и 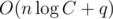 дополнительной памяти.
дополнительной памяти.
Опишем жадный алгоритм, который позволяет решить задачу при k > 2 для любой строки S.
Будем считать, что мы всегда переворачиваем некоторый префикс строки S (возможно, длины 1, подробнее ниже). Поскольку мы стремимся минимизировать строку лексикографически, легко убедиться в том, что мы будем переворачивать такие и только такие префиксы, префикс которых (после переворачивания) совпадает с минимальным лексикографически суффиксом перевернутой строки S (обозначим ее Sr), в частности, это префикс, совпадающий по длине с минимальным суффиксом Sr (операция переворачивания префикса S равносильна замене его суффиксом Sr соответствующей длины).
Обозначим минимальный лексикографически суффикс строки Sr как s. Можно показать, что никакие два вхождения s в Sr не пересекаются, так как в противном случае строка s была бы периодической, и минимальный суффикс имел бы меньшую длину. Значит, строка Sr имеет вид tpsaptp - 1sap - 1tp - 2... t1sa1, где sx означает конкатенацию строки s x раз, a1, a2, ..., ap — натуральные числа, а строки t1, t2, ..., tp — некоторые непустые (кроме, возможно, tp) строки, не содержащие s в качестве подстроки.
Перевернув некоторый подходящий префикс строки S, мы перейдем к меньшей строке S', при этом минимальный суффикс s' этой перевернутой строки S'r не может быть лексикографически меньше, чем s (это каждый может доказать самостоятельно), поэтому мы стремимся сделать так, чтобы s' осталось равным s, что позволит увеличить префикс вида sb в ответе (а значит и минимизировать его). Легко доказать, что максимальное b, которое мы можем получить, равно a1 в случае p = 1 и 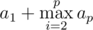 (в случае, если p \geq 2$). Действительно, после таких операций префикс ответа будет выглядеть как sa1saitisai - 1... sa2t2. Поскольку t_{i} — непустые строки, увеличить количество конкатенаций s в префиксе ответа никак не получится. Заметим, что переворот второго префикса (sai...) возможен, так как k > 2.
(в случае, если p \geq 2$). Действительно, после таких операций префикс ответа будет выглядеть как sa1saitisai - 1... sa2t2. Поскольку t_{i} — непустые строки, увеличить количество конкатенаций s в префиксе ответа никак не получится. Заметим, что переворот второго префикса (sai...) возможен, так как k > 2.
Из описанных выше утверждений следует, что при k > 2 для оставшейся строки всегда следует переворачивать префикс, который после переворота совпадает с суффиксом строки Sr вида sa1. Чтобы находить этот суффикс каждый раз, достаточно один раз построить декомпозицию Линдона (с помощью алгоритма Дюваля) перевернутой исходной строки и аккуратно объединять равные строки в ней. Единственным случаем остается вариант, когда префикс оставшейся строки переворачивать не нужно — его можно обработать как конкатенацию последовательных переворачиваемых префиксов длины 1.
Поскольку для k = 1 задача тривиальна, осталось решать задачу для k = 2, то есть деление строки на две части (префикс и суффикс) и какой-то способ их переворачивания. Случай, когда ничего не переворачивается, нам не интересен, рассмотрим два других случая:
Префикс не переворачивается. В таком случае обязательно переворачивается суффикс. Два варианта строки с перевернутым суффиксом можно сравнивать за O(1) с помощью z-функции строки Sr#S.
Префикс переворачивается. Для решения этого случая можно воспользоваться утверждениями из разбора задачи F Яндекс.Алгоритма 2015 из Раунда 2.2 авторства GlebsHP и рассмотреть только два варианта поворота префикса, перебрав для каждого из них все два варианта поворота суффикса.
Остается выбрать из двух случаев лучший ответ. Итоговая асимптотика решения O(|s|).











C за O(NK2) можно решить: переберем какой-то магнит, удалим всем магниты левее его, переберем значение x и удалим все магниты правее x (всего K таких значений), и переберем y и удалим все магниты выше y (таких тоже K). Далее удалим максимальное количество магнитов с минимальным y. Удалять\восстанавливать магниты можно за O(1), поддерживая массивчик used[N], сколько раз попал под удаление i - ый магнит (может быть удален как со слишком большим x и со слишком большим y 2 раза и т.п.).
В задаче Div2.B, не совсем понятно как учитываются цифры делящиеся на x, но начинающиеся с y, ведь количество цифр начинающихся с y-1 точно такое же как с y. Я решал эту проблему бинарным поиском, находя максимальное и минимальное числа начинающиеся с y и делящиеся на x, не могли ли бы вы рассказать подробнее?
Формула включений-исключений.
Берём абсолютно все числа менее 10^k, которые делятся на х.
Добавляем все числа менее y*10^(k-1), которые делятся на х (если у — не нуль).
На этот момент все числа, которые начинаются на цифру меньше чем у, посчитаны дважды.
Вычитаем все числа менее (y+1)*10^(k-1), которые делятся на х.
Все числа, начинающиеся с у, теперь не посчитаны. Все нужные числа, которые были взяты дважды, теперь посчитаны один раз. Значит это ответ.
Спасибо, понял.
Кто-нибудь может пояснить из каких соображений получается это утверждение?
Из таких что синус а в pi/2 достигает максимума, а значит максимально срезать будет расстояние нам как раз когда точка вверху. Ну и sin x=sin(pi-x), кроме того он растёт с -pi/2 и потом ровно так же убывает до 3*pi/2. Поэтому быстрее всего будет достигнут результат если брать отрезок [pi/2-x; pi/2+x]. Если у нас меньше одного полного круга.
В первом случае (точка посередине вверху) колесо сделает чётное количество полных оборотов, во втором случае (когда внизу) — нечётное. Можно даже ещё упростить: отдельно обработать все полные обороты. Там скорость просто v. Отдельно — оставшуюся дистанцию до полного оборота.
Свойства синуса из школьной программы — ОК согласен. Момент как из свойств синуса получается процитированное свойство дистанции не прояснился.
Таким образом, что этот синус добавляется к дистанции, пройденной колесом. Дистанция, пройденная точкой — это есть дистанция, пройденная колесом, плюс этот самый синус. Это то же самое как если бы колесо не катилось, а двигалось за счёт, если угодно, параллельного переноса вдоль ОХ, а точка равномерно перемещалась бы по колесу. То есть её проекция на ОХ так высчитывается как положение самого колеса и положение точки на колесе. На положение колеса мы повлиять никак не можем, можем только получить халявный бонус к дистанции за счёт положения точки, а оно определяется тем самым синусом.
Можно подробнее пожалуйста, не могу понять
Координата датчика вычисляется как сумма координаты центра колеса и координаты датчика относительно центра колеса. То есть
xd(t) = xc(t) + r * sin( v * t / r ), если в нулевой момент времени датчик в самой верхней точке колеса. Если продифференцировать это равенство по времени, получим выражение для скорости датчика:vd(t) = v + v * cos( v * t / r ). То есть всегда скорость датчика от0до2v. А максимальна она как раз получается, когда датчик сверху колеса. Поэтому из наивных соображений можно догадаться, что за данный период времени надо чтобы как можно больше раз датчик был в верхней точке (и как можно меньше раз в нижней, когда скорость0). Ну и отсюда догадываемся, что картинка должна быть симметричной.Однако, это пока что ниоткуда не следует. Это можно обосновать чем-то вроде выпуклости циклоиды. Но разбор, в котором ничего такого не доказывается достоин фейла, из-за которого раунд нерейтинговый. Потому что, видимо, этим доказательством авторы тоже не занимались.
Красавчик! А скажи еще, пожалуйста, если в данном решении сказали все данные, которые однозначно определяют положение датчика на концах интервала, то зачем здесь бинарный поиск? Разве нельзя сразу посчитать ?
Нельзя, потому что нужно посчитать не функцию типа
x + sin( x ), а обратную. А она так просто не выражается, зато монотонна и бинпоиск работает.Ммм, я видимо один, у кого возникли проблемы с написанием точных формул в Div2-B, настолько, что решил написать бинпоиск? :D
Задачу D не писал, интересно лишь отсекалась ли корневая по времени, когда мы сортируем все запросы по паре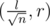 и явно поддерживаем количество по каждому простому и текущий ответ?
и явно поддерживаем количество по каждому простому и текущий ответ?
Даже если отсекалась, то не отсеклась) У меня за 2 секунды зашло.
В чем была проблема с задачей C? (div 2)
авторское решение неправильно работало в случае нечетных n.
Будет ли обзор задачи DIV1A? Было бы интересно почитать решение для четных n и узнать почему для нечетных оно не работает и как надо.
Просто посмотрите еще раз, решение уже давно есть.
Div1A: Ответ — не максимум среди значений, а минимум.
Is the solution for the third task correct ?
From the other thread...
Consider the case
Their algorithm seems to give the wrong answer 2, while if player 1 banned a 1 or 5 at the beginning, it would be possible to get difference 1.
Yes I think so, but I can not understand why the wrong solution is written? It looks like my solution on the contest maybe we miss some 'new' part.
"n is always even". This statement was added to the new version of the problem. The greedy solution only works if n is even.
In this problem ,n is even. So your case will not occur.
I don't understand Div1 B. Please elaborate.
Let's normalize d, r, v so that r = 1, d = dorig / rorig, v = vorig / rorig. This will not change the time taken. Observe that for every 2π distance, the sensor rotates exactly 1 round so the sensor's position doesn't matter and time taken is 2π / v. We only need to consider the remainder of d / 2π, lets call this d′.
Since it takes (2π / v)s to rotate 2π radians, rate of rotation is v radians/s. Then, if the sensor is at the topmost position at time t=0, at time t, it would have moved vt as a result of horizontal velocity from v, and sin(vt) as a result of rotation. (For 0 ≤ t ≤ π / v). So d = vt + sin(vt). Now, the speed of the sensor is fastest when it is at the top of the wheel and slowest at the bottom (you can check this by taking the 1st derivative of the equation), and speed vs time graph is symmetrical around t=0, therefore the sensor should be at the top of the wheel at the midpoint of the distance.
Finally, to solve the problem, binary search the value of t to satisfy the equation x = vt + sin(vt), where x = d′ / 2, and multiply by 2 due to symmetry.
"speed vs time graph is symmetrical around t=0, therefore the sensor should be at the top of the wheel at the midpoint of the distance."
Why top at midpoint of distance?
I want to explain it by using mathematical calculation. We start with the initial phase $$$\theta$$$. The equations of motion is: $$$s(t)=r\cos(\theta+\frac{v}{r}t)+vt$$$. We set $$$L=f-s$$$. Then we have:
$$$vt+r(\cos(\theta+\frac{v}{r}t)-\cos\theta)-L=0\ ...(1)$$$.
Consider the function $$$t=t(\theta)$$$. We want to minimize $$$t$$$, so we have $$$\frac{dt}{d\theta}=0$$$. Then we will get:
$$$vt'+r(-\sin(\theta+\frac{v}{r}t)(1+\frac{v}{r}t')+\sin\theta)=0$$$.
We have $$$t'=0$$$. So $$$\sin(\theta+\frac{v}{r}t)=\sin\theta\ ...(2)$$$.
According to $$$(2)$$$, We will discussion two cases:
Case 1. $$$\frac{v}{r}t=2k\pi$$$ with $$$k\in Z$$$. By considering $$$(1)$$$ we can get $$$L=vt$$$. So $$$L=2k\pi r$$$. Since $$$L$$$ and $$$r$$$ are positive integers, this case will never be happened.
Case 2. $$$\theta+\frac{v}{r}t+\theta=(2k+1)\pi$$$ with $$$k\in Z$$$. By considering $$$(1)$$$ we have:
$$$vt-2r\sin(k+\frac{1}{2})\pi \sin(\frac{v}{2r}t)-L=0$$$.
Finally, we have: $$$vt\pm 2r\sin(\frac{vt}{2r})-L=0$$$.
By analyzing the derivative we know that it is monotonic. So we can using binary to get the answer.
Can someone please explain Div2C. Grammar written is really really poor. How is it possible for player 2(archer) to always make n/2-1 consecutive bans? Also the answer of the question's test case doesn't satisfy max(arr[I+n/2]-arr[I]).
As far as I understand, it must be minimum(arr[i+n/2] — arr[i]).
And I'm not really sure about the explanation in the editorial, but it looks like the strategy of the second person is to remove the median. For example, if the second player had 7 places to choose from, he would pick 4th. If he keeps doing, he would get consecutive bans. (It will be obvious if you actually try this strategy) However, I'm not sure why this is an optimal solution.
I think i figured it somehow. Let the final positions of warrior and archer be L and R. There cannot be more than n/2-1 bans between (L-R). Since that would include bans from warrior as well. But if warrior plays optimally he can always avoid a ban between L-R to reduce the distance L-R. So it shouldn't be hard to conclude that optimal strategy for warrior is if it bans all the corner-most positions from the array.
Now the only case left is bans<=n/2-1 between L-R (Which are bans of archer only) Now we can prove that there cannot be less than n/2-1 bans between L-R. Since if archer plays optimally(i.e no matter what the warrior bans, if it bans the median) the archer can always make n/2-1 bans between L-R which is the best case for the archer.
E.g :
6 1 2 3 4 5 6 W: 6 A: 3 (Median of 1 2 3 4 5) W(Left 1 2 4 5): 1 A: 4 (Median of 2 4 5) Left 2 and 5, ALL the possible bans between 2 and 5 are of the Archer.
So archer will always get the range L-R = n/2-1. Now best strategy for warrior is to chose such corner cases so that it minimizes this n/2-1 distance.
Thus, the answer should be min(arr[i+n/2]-arr[i]). Tell me if i'm wrong. Thanks.
In your A's tutorial, "Thus the answer is the maximum between every of …… values." It should be minimum, isin't it?
В задаче A div 1 в разборе не встречается слово "четный". Хотя это наверное важно. Объясните пожалуйста, что не так с нечетными n? Или дайте контр тест.
UPD: Я все понял
.
Div 1, C! Tried a lot but gives runtime error. Maybe stack space exhausts! Can anyone help me out ? Code
Step-by-step guide to solving 594D - REQ:
Read input, including queries to solve them offline. Sort the queries by $$$l$$$, making sure to keep their original indices.
Use Sieve of Erastosthenes to precalculate primes up to $$$1000$$$ $$$(\geq \lfloor \sqrt {\max a_i} \rfloor)$$$
Use those primes to factorize all the values of $$$a$$$ (this step takes $$$O(168n)$$$). We want to store the results in two data structures:
Initialize a BIT or segment tree ($$$B$$$), that can calculate range products modulo $$$10^9 + 7$$$, with the values from $$$a_i$$$.
Use $$$M$$$ to find the leftmost index for each prime factor. Multiply those positions in $$$B$$$ by $$$\frac {p-1} p$$$.
We can now answer queries with $$$l = 1$$$ using $$$B$$$. To "advance" $$$l$$$ by $$$1$$$ to eventually answer the rest of the queries:
Sample: 65793661