Можно прокрутить пост до низу и прочитать доказательство корректности построения суммы Минковского, которе недавно обсуждалось на КФ.
Задача DIV1-A, DIV2-C Поезда.
К этой можно было подойти с двух сторон - как программист и как математик. Рассмотрим оба подхода.
Сначала запишем несколько общих суждений. Поставим на прямой все моменты времени, в которые приходят поезда. Будем относить отрезок между двумя соседними точками к той девушке, к которой идет поезд, соответствующий правому концу отрезка. Также заметим, что вся картина периодична с периодом lcm(a, b). Очевидно, что Вася будет чаще ездить к той девушке, суммарная длина отрезков которой больше.
Программистский подход заключается в моделировании процесса. Если нам надо сравнить длины двух множеств отрезков - давайте их посчитаем. Это делается с помощью двух указателей. Смотрим какой поезд поезд приедет следующим, прибавляем время до прихода этого поезда к одному из ответов, двигаем указатель и текущее время. Остановиться стоит либо когда два последних поезда пришли одновременно, либо когда пришло a+b поездов. Решение за O(a + b),что с запасом укладывается в ограничение по времени. Не забываем, при этом, что lcm(a,b) ~ 10^12, то есть нужен 64-битный тип данных.
Математический подход позволяет получить более изящное и короткое решение, однако придется больше подумать. Кажется очевидным, что чаще Вася будет ездить к той девушке, к которой чаще ходят поезда. Этот факт почти верен. Попробуем его доказать. Сократим периоды a и b на их gcd - от этого, очевидно, ничего не изменится. Пусть для определенности a ≤ b. Посчитаем суммарную длину отрезков, соответствующих второй девушке. Для этого заметим несколько фактов.
1) Все они не превосходят a
2) Все a отрезков различны (из-за взаимной простоты).
3) Все они хотя бы 1.
Но такое множество отрезков - единственное и его длина равна 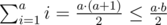 . Причем равенство достигается при b - a = 1. Значит верно следующее. Ответ равен Equal, когда |a - b| = 1, иначе чаще Вася ездит к девушке к которой чаще ходят поезда. Главное не забыть поделить a и b на их gcd.
. Причем равенство достигается при b - a = 1. Значит верно следующее. Ответ равен Equal, когда |a - b| = 1, иначе чаще Вася ездит к девушке к которой чаще ходят поезда. Главное не забыть поделить a и b на их gcd.
Задача Div1-B, Div2-D Вася и Типы.
В этой задаче нужно было написать ровно то, что написано в условии задачи, практически за любую сложность.
Предлагается делать это так. Для каждого типа данных будем хранить два значения – его имя и количество звездочек при его приведении к void. Тогда запрос typeof обрабатывается пробегом по массиву определений, в котором мы находим нужное нам имя типа, и количество звездочек в нем.
Тип errtype удобно хранить как void, к которому приписали - inf звездочек.
Таким образом, выполняя запрос typedef, мы находим количество звёздочек при типе A, добавляем к нему количество звездочек и вычитаем количество амперсандов. Не забываем заменять любое отрицательное число звездочек на - inf, и создавать новое определение типа B, удаляя старое.
Задача Div1-C, Div2-E Интересная игра.
В этой задаче нужно провести анализ игры. Однако, из-за того что каждым ходом игра распадается на несколько независимых, анализ можно провести с помощью функции Гранди (можно почитать здесь, здесь или здесь). Остается построить переходы для каждой позиции. Можно строить переходы отдельно для каждой вершины, решая O(sqrt(n)) несложных линейных уравнений. Можно построить все разбиения заранее, просто перебирая наименьший член и количество, и вылетая, когда сумма превосходит n. Второй способ лучше, потому что он работает за O(m + n), где m - количество рёбер, а первый - за O(nsqrt(n)), что побольше.
Оценим m в максимальном тесте. Рёбер - не более 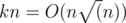 . Однако на практике их гораздо меньше - порядка 520 тысяч. Соответственно, рёбра вполне можно успеть построить за время O(nk).
. Однако на практике их гораздо меньше - порядка 520 тысяч. Соответственно, рёбра вполне можно успеть построить за время O(nk).
Можно попытаться посчитать функцию Гранди по определению - ксоря все нужные значения для каждой позиции. Но такое решение не проходит - слишком много длинных разбиений.
Научимся для длинного разбиения быстро считать ксор функций Гранди. Используем стандартный прием для подсчета функций на отрезке - xor[l, r] = xor[0, r] xor[0, l - 1]. По ходу алгоритма будем поддерживать в xor[i] ксор на префиксе до i. Тогда и ксор на отрезке можно посчитать за O(1). Решение получилось строго за количество рёбер, которое не очень велико.
Задача Div1-D. Красивая дорога.
В этой задаче надо для каждого ребра посчитать количество путей, на которых оно является максимальным. Так как для одного ребра отдельно не кажется возможным посчитать ответ быстрее, чем за линейное время, решение будет обрабатывать все ребра вместе.
Решим задачу сначала для двух крайних случаев, потом, объединив эти два, получим полное решение.
Первый случай - когда веса всех ребер одинаковы. В таком случае можно решить задачу обходом в глубину. Для каждого ребра нам просто нужно посчитать количество путей, которые проходят по этому ребру. Это количество есть произведение количеств вершин по разные стороны ребра. Если мы посчитаем количество вершин с одной стороны от него, тогда зная общее количество вершин в дереве, легко найти количество вершин по другую сторону от него, а значит и требуемое количество путей, на которых оно лежит.
Второй случай – когда веса всех ребер различны. Отсортируем ребра в порядке возрастания веса. Изначально возьмём граф, в котором нет рёбер. Будем добавлять по ребру в порядке возрастания веса, для каждого ребра объединяя компоненты связности, которые оно соединяет. Тогда ответ для каждого нового добавленного ребра – произведение размеров компонент, которые оно соединило.
Теперь надо объединить эти два случая. Будем добавлять ребра по возрастанию, но не по одному, а группами одинокого веса. Поймём, что является ответом для каждого из добавленных рёбер. После добавления наших рёбер образовалось некоторое количество компонент связности - для каждого ребра мы считаем то самое произведение количеств вершин по разные его стороны внутри его новообразовавшейся компоненты связности.
Для того, чтобы посчитать это самое количество рёбер по разные его стороны, поймём, что от старых компонент связности достаточно знать лишь их размеры, и связи между ними - то, как они были устроены нам не важно. Воспользуемся системой непересекающихся множеств: добавляя рёбра в наш лес мы объединяем старые компоненты связности по этим рёбрам. Заметим, что до объединения компонент мы должны посчитать ответ для наших рёбер - а это можно сделать обходом в глубину на нашем сжатом дереве как в первом случае, только вместо количества вершин по разные стороны от ребра мы берём сумму размеров компонент связности по разные стороны от ребра.
Как это аккуратно реализовать:
- Сжатый граф проще всего динамически создавать на каждом шаге: в нём будет O(E’) вершин и рёбер, где E’ - количество добавляемых рёбер исходного дерева.
- В новом создаваемом сжатом графе не создаём ненужных вершинок: DFS работает всё-таки за O(V + E), а не за O(E), поэтому незадействованные компоненты связности мы в обход не включаем.
- Пользуемся 64-битным типом данных. Для хранения ответа порядка (105)2 он подойдет больше чем 32-битный.
- Не сливаем явно списки смежности при соединении компонент. Это слишком долго.
- Можно вместо массивов делать всё на vector’ах / map’ах / динамической памяти, чтобы суммарное время обнуления массива пометок для DFS’а занимало O(V). Либо вместо обнуления массива пометок держим вместо булевского флага номер итерации. И вообще, лучше не обнулять лишних массивов. Все таки алгоритм может делать V итераций.
- Осторожно, решение с map работает на пределе TL, поэтому его надо писать очень аккуратно, лучше использовать вектора + список задействованных вершин. Авторское решение с map укладывается в TL с запасом всего в полсекунды. В то время как использующее вектора имеет четырёхкратный запас по времени.
Задача Div1-E. Идол Могоху-Ри.
В этой задаче надо было проверить, что точка являться центроидом треугольника образованного точками из данных трех многоугольников. Переформулируем задачу. Надо проверить существование трех точек A,B,C, таких, что A принадлежит первому многоугольнику, B – второму, C – третьему, и
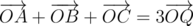 . Вполне логично, что надо понять какое множество точек задает это
. Вполне логично, что надо понять какое множество точек задает это 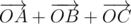 , научится его строить и проверять точку на принадлежность ему. Такое множество называется суммой Минковского. Из его свойств нам понадобится только одно: сумма двух выпуклых многоугольников - выпуклый многоугольник, причем стороны многоугольника совпадают, как вектора, со сторонами исходных многоугольников. Докажем это позже.
, научится его строить и проверять точку на принадлежность ему. Такое множество называется суммой Минковского. Из его свойств нам понадобится только одно: сумма двух выпуклых многоугольников - выпуклый многоугольник, причем стороны многоугольника совпадают, как вектора, со сторонами исходных многоугольников. Докажем это позже. Как теперь этим пользоваться? Первое что нам дает это свойство - алгоритм проверки на принадлежность. После того как сумма будет построена проверять точку на принадлежность сумме можно стандартным алгоритмом проверки точки на принадлежность выпуклому многоугольнику за логарифмическое время. Кроме того сразу же получается и алгоритм построения. Надо просто сложить координаты самых нижних (из них самых левых) точек всех трех многоугольников. В результате мы получим точку, являющуюся нижней левой для последнего многоугольника. А стороны получаются как отсортированный по полярному углы список сторон исходных многоугольников (вместо сортировки сливать отсортированные массивы).
А теперь самая вкуснятина:
Доказательство.
Доказывать свойство будем для дух выпуклых многоугольников M1 и M2. Сумму обозначим за M.
Докажем корректность алгоритма для двух многоугольников, для трёх многоугольников доказтельство никак не поменяется. Пусть первый многоугольник - А, второй - B. Пусть сумма Минковского - M.
Докажем, что M - выпуклое множество.
Выберем некоторые
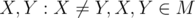 . По определению
. По определению 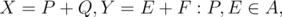 Q,
Q, 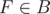 (здесь и далее точка отождествляется со своим радиус-вектором).
(здесь и далее точка отождествляется со своим радиус-вектором). Пусть некоторая точка
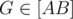 . Докажем, что
. Докажем, что 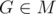 .
. Т. к. G лежит на [AB],
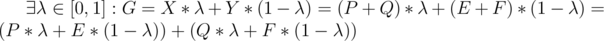 .
. Заметим, что первая скобка, очевидно, есть некоторая точка, лежащая на отрезке [PE]. А значит, точка, лежащая внутри многоугольника A, так как тот - выпуклый. Аналогично, вторая скобка лежит внутри B. Значит их сумма, то есть G, лежит в сумме Минковского. А значит, сумма Минковского есть выпуклое множество.
Рассмотрим некоторую сторону XY первого многоугольника. Повернём плоскость так, чтобы сторона XY оказалась горизонтальной и чтобы многоугольник лежал сверху от прямой XY
Рассмотрим самую нижнюю горизонтальную прямую, пересекающую B. Пусть она пересекает B по отрезку PR, где точка P не правее R (понятно, что PR может оказаться вырожденным отрезком из одной вершины). Назовём PR самым низкий отрезком многоугольника. Построим по аналогии самый низкий отрезок UV многоугольника M.
Докажем, что
 - в противном случае
- в противном случае 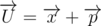 . Понятно, что x и p - самые нижние точки многоугольников A и B - в противном случае одну из них можно сдвинуть на малый вектор d, лежащий в нижней полуплоскости, так, что точка останется внутри своего многоугольника. При этом U сдвинется так же на d, что противоречит тому, что U - одна из нижних точек многоугольника.
. Понятно, что x и p - самые нижние точки многоугольников A и B - в противном случае одну из них можно сдвинуть на малый вектор d, лежащий в нижней полуплоскости, так, что точка останется внутри своего многоугольника. При этом U сдвинется так же на d, что противоречит тому, что U - одна из нижних точек многоугольника. Значит, x и p - нижние точки своих многоугольников. Аналогично, x и p - самые левые точки на нижних отрезках своих многоугольников - в противном случае сдвигаем x или p на вектор d, направленный влево, вновь получая противоречие - точка U перестаёт быть самой левой из нижних.
Значит, U = X + P. Аналогично V = Y + Q. Значит,
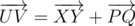 .
.Тем самым, последовательность сторон M как векторов в порядке обхода, например, по часовой стрелке, есть как раз объединение сторон M1 и M2 как векторов в порядке обхода по часовой стрелке, что сразу доказывает корректность алгоритма.











> Можно попытаться посчитать функцию Гранди по определению - ксоря все нужные значения для каждой позиции. Но такое решение не проходит - слишком много длинных разбиений.
У меня самый тупой Шпрага-Гранди(причем рекурсивный) прошол=)
У нас была идея ограничить сверху количество кучек в разбиении, чтобы спастись от прекальков. Но тогда ломался xor на отрезке..
Мы не сговаривались о размере, честно :-)
Sorry, we are soo sleeppy...
P. S. Чувствую себя как-то неуютно. Сам оранжевенький, втолковываю что-то красненькому. Ну вот зачем было сливать тур перед своим раундом?)
"Thus, the sequence of sides M as vectors in the, for instance, counterclockwise order, is nothing other than the union of sides of A and B as vectors in the clockwise order, that immediately proves the correctness of the algorithm.”
Yes, you're right. Fixed.
===
Well, there exist at least one human, who read that up to the end :-) Great.
thank you for good editorial. can you say what do you mean by position in problem Div1-C? Do you mean the size of each pile or some piles together?
Like in all problems that are solved using Grundy function, here position means "One pile of fixed size". It is true that if we have some piles of different sizes then games on each of them are independent — that's also the explanation why xoring of Grundy functions works correctly.
Thanks! I think i get the main idea of the solution!
For Div 2 C — Trains, is there a proof for the fact that the segment lengths will be different (as mentioned in the editorial)?
Yes, this can be proved by using the basic concepts of number theory. Let b > a, After dividing a and b by their gcd let new a = a/g, and new b = b/g, where g = gcd(a,b)
Now gcd(a,b) = 1. Let's calculate for each instance b, 2*b,.....a*b, the length of the segment.
For a*b the length of the segment will a. For i * b, i < a the length of the segment will be (i*b)mod a.
Let for two different instances i, j < a, the length of the segment is the same.
so i*b ≡ j*b mod a => i ≡ j mod a, as gcd(a,b) = 1, which is not possible as i and j are two different instances.
Thus the contradiction proves, for two different instances, the length of the segment cannot be the same.
A very clearly stated explanation. Thanks for the help!
I understand everything, but why Vasya has two girlfriends?
For problem C div 1 I found another solution. First of all the divisions are in the following form:
So, we iterate over the lengths of the segments and then iterate over the sum of its elements by just adding the large of the segment (this takes n log(n) of time because it is the armonic sum) to the sum of the element we add an arist in the form {init_segment, init_segment + length — 1}. For example, we have (2, 3, 4) with sum 9 so to nine we add the segment (2, 4).
Now, we iterate over all the numbers in the range $$${1, \dots, n}$$$ and we iterate over its segments that we precomputed in the armonic sum. To get the xor of the segment we can use a segment tree and just query the segment that has and we make a xor, then we update the grundy number in the segment tree of the current element. With this we just get the grundy number of each number.
Finally, if the grundy number of $$$n$$$ is 0 then first player lost and if the grundy number is greater than 0 then we get the segment with shortest length which has grundy number 0.
With this code you can solve the problem in $$$O(n log(n)^2)$$$ because the sum of the edges are at most $$$n log(n)$$$ and we make a query in the segment tree over each segment that is $$$n log(n)^2$$$ :).