Построить для задачи A такую задачу B, чтобы они друг к другу сводились (ну или хотябы A сводилась к B, и B визуально была не сильно сложнее), и при этом задача B формулировалась как можно проще.

Прием 4 немного сомнителен :)

Прием 2 стоит отдельного поста. Очень часто работает убирать ограничения, фиксировать константы, считать числа простыми и так далее, кроме того, это отсекает очень много неприменимых методов для приема 6.

Прием А: "попытайтесь обобщить задачу". Как прием 2, только наоборот. Например, на одном NEERC была задача, в которой нужно было считать подотрезки массива, для которых побитовая сумма по модулю два равна побитовому и. А что, если это произвольные операции? Такая задача звучит совсем страшно. Значит, есть какая-то особенность в операциях. Внимательно смотря их, находим, что значение побитового и на отрезке меняется не более числа бит раз при пополнении отрезка. Дальше — дело техники.

Прием Б: "уменьшайте произвольность". Например, порядок чисел ввода не важен — рассмотрите числа в порядке, в котором удобнее. Кажется банальностью, но очень часто забывается.

Прием В: "ищите факты". В поисках помогает прием А, 2, опыт и сокомандники. Если в задаче есть операция, часто полезно искать ее инварианты. Если в задаче (региональный этап 2014 года, задача 8) сильно связный турнир — порисуйте, рано или поздно заметите, что в нем всегда есть гамильтонов цикл. Если задача не похожа на стандартную, ключевой факт в ней обычно есть.

Прием Г: "знайте сильные методы". Некоторые методы, вроде hevy-light и центральной декомпозиции дерева, персистентной дерамиды, пары стандартных sqrt-декомпозиций и суффиксного дерева настолько сильные, что решают почти все задачи в некоторой области. Обычно они, что называется, слишком много букв для этой задачи, но когда нечего делать, можно просто сесть и написать. И надеюсь, я никогда не буду решать контест, в котором авторское решение будет использовать персистентную дерамиду, записанную в вершинах суффиксного дерева.

Прием Е: "это динамика". Не приспособлен для частого применения. Ваш сокомандник говорит вам: "я придумал, это динамика". Вы тут же понимаете, какая, рассказываете. Ваш сокомандник отвечает: "круто, а я пошутил".

"Принцип узких мест"

Представьте что вам нужно поймать человека, который едет на машине от ВДНХ к МГУ, хотя вы понятия не имеете как он поедет, он точно будет в какой-то момент переезжать через Москву-реку, поэтому поставим засады на всех мостах. Можно применить схожую идею к решению задач, хотя это во много перекликается с пунктом 2: "не знаю как будет устроена эта структура, но она точно будет уметь отвечать на запрос суммы и порядковой статистики, где бы мне такую взять?"

A bunch of answers on Quora (including one from me).

Опишу два моих приёма.

Частный случай приёма 4. Пусть у нас есть объекты с какими-то свойствами, например, элементы массива с позицией и значением. Назовём эти свойства координатами X и Y, нарисуем их на плоскости, попробуем переформулировать задачу в геометрических терминах — вдруг надо найти что-то очевидное? Другой пример: для событий на прямой можно считать X — координатой на прямой, а Y — временем, тогда красиво выражаются всякие условия вроде "у нас ограничена скорость движения по прямой" (а если еще и аффинное преобразование сделать, вообще получим что-то на углах в 90 градусов). Еще пример: если у нас есть объекты разной стоимости и веса и надо что-то считать или узнавать про средние значения в каких-то подмножествах, можно наверняка свести к задаче про центр тяжести и применить физического капитана Очевидность (например, "центр тяжести лежит в выпуклой оболочке" или "любую точку внутри или на границе выпуклой оболочки можно получить в качестве центра тяжести при неотрицательных весах, и только их").

Двойственный приём: свести всё к безликим буквам и формулам. Работает нечасто, у меня обычно срабатывал в задачах на строки, где есть какая-нибудь динамика. Берём формулу перехода, записываем в алгебраической форме, что-то сокращаем, что-то перегруппировываем, в какой-то момент обнаруживаем, что у нас всё распалось на сумму независимых кусков, каждый из которых по отдельности можно быстро и понятно найти. Например, подсчитав какой-то кусок в отдельной динамике. При этом физический смысла у этих кусков может быть в стиле "гармоническое среднее рейтинга на Codeforces и TopCoder с коэффициентами sin 2 и cos 6", но ничего страшного. Главное — не запутаться в буквах по дороге.

Еще парочку приемов:

0) Перечитать задачу еще раз. Если идет непроходимый ступор — очень часто спасает. Вернее, следующая комбинация. Перечитать задачу. Посмотреть на ограничения. Перечитать задачу. Посмотреть на семплы. Перечитать задачу. Прокрутить, как это связано. Перечитать задачу. Нарисовать несколько тестов. Перечитать задачу...

1) Уйти в сторону от задачи. Может быть, есть смысл подумать, зачем автор включил эту задачу в контест. Может быть, стоит попытаться решить какую-то другую задачу вместо этой. Не с более маленькими ограничениями, а вообще другую, с другим условием. Может быть, нам это как-то поможет. Понимаю, что это достаточно расплывчатый совет, но нужно, наверное, интуитивно чувствовать, когда и как стоит это попытаться применить.

Прием 2, как было написано, стоит отдельного поста. Попробую рассмотреть то, какими именно вариантами можно применять этот пункт, и заодно найдем еще вариант решения:

1) Ограничения сделать более простыми. Допустим, в задаче есть ограничения n = 100500, m = 300228. Становится понятно, что задачу в таких случаях нужно решать за O((n + m) * log(n)), O((n + m)(3 / 2)) или быстрее. Ну, в крайнем случае можно накинуть еще логарифм сверху, но это уже нужно будет упихивать. Попробуем решить эту задачу за O(n²). Получилось? Тогда, может, можно заменить это какой-то структурой данных? Или заметить, что стоит рассматривать не все переходы, а только, допустим, делители числа n? Не получилось решить за O(n²) — решаем за куб! Если этого не получилось — может, мы хотя бы с помощью перебора можем найти ответ? Не получилось так — давайте попробуем поиграться с другими ограничениями: что, если все числа влазят в int? И так далее. Рано или поздно, мы сможем найти решение хоть для какого-то варианта, хотя бы сможем понять, как получается семпл)

И в этот момент рождается еще один вариант, как можно придумать решение задачи. Ведь перебор-то, особенно для маленьких тестов, мы можем вполне и у себя в голове прокрутить. Сгенерируем маленький тест. Если это граф — нарисуем его на бумажке, и попробуем применить наш перебор(вообще говоря, это может быть и не перебор). Распечатка тут зачастую не годится — ведь ты не знаешь заранее, что ты должен распечатать. Может, это состояние в вершинах. А может, в ребрах. А может, это вообще какое-то хитрое произведение вершины на квадрат веса ребра и на номер этой вершины в обходе, зависящем от фазы луны. Это можно выяснить только прокрутив решение в голове. Далее, как только мы получили с помощью перебора ответы на тест — пробуем применять смелые идеи. И, опять-таки, не стоит торопиться распечатывать. Потому что, рисуя и прокручивая идею на бумажке, мы не просто какие-то цифры выводим — мы видим, как они получаются, и где конкретно у нашей смелой идеи возникли затруднения Вполне возможно, что и тест сойдется — но, прокручивая идею в голове, мы поймем, что, например, если бы у ребра был вес не 6, а, например, 7 — ничего бы не сошлось. А при весе 8 опять бы сошлось. Так что распечатывание, безусловно, разгружает руки и голову — но иногда голову и руки полезно загрузить, хотя бы на мелких тестах.
В ходе такого мыслительного процесса может возникнуть понимание, что на малых тестах проблемы возникнуть не может. Зато может возникнуть на больших. Тогда уже можно распечатать и посмотреть — ведь мы уже знаем, где искать проблему.
Я бы этот метод назвал бы "поставить себя на место нашего решения". Это все-таки отличается от метода "поставить себя на место задачи", хотя иногда может и совпасть с этим методом. Вернемся все-таки к пункту 2

2) Ограничения сделать более жесткими. Казалось бы, глупость. Но иногда бывает, что при более жестких ограничениях задача решается проще. Вот только не совсем с той асимптотикой, которую бы хотелось... Тогда возвращаемся к идее решения "поставить себя на место решения" и попробуем понять, что с этим можно сделать. В комбинации с первым методом(кое-что упрощаем, кое-что усложняем) работает замечательно, если мы правильно выстроим цепочку упрощений-усложнений.

3) Вид структуры. Как было уже сказано, вместо дерева делаем путь, вместо графа — дерево или двудольный граф, вместо строки — число. Далее все, как уже было выше. Ну и различные комбинации того, что было сказано выше.

На котестах у меня есть выбор или думать или писать решения, поэтому я пишу решения. Если я начну их придумывать у меня просто не будет времени их запрогать...

Помогите найти контртесты плиз: http://codeforces.me/blog/entry/20556

Предположить, что ответ Х. Применяется скорее в купе с другими приемами как Прием 6: "Подбери метод" или со вторым приемом из http://codeforces.me/blog/entry/20548?locale=ru#comment-252650

В некоторых случаях, если зафиксировать ответ и поиграться с формулой, то можно переформулировать задачу во что-то более решаемое. На ум приходит 236. Greedy Path. В ней требуется найти цикл максимизирующий: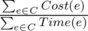 . Допустим у нас есть субоптимальный ответ A и мы хотим проверить, можем ли мы найти что-то лучше, тогда можно немного поиграться с неравенством:

Если за стоимость ребра принять  - Cost(e) + A·Time(e), то это уже более известная задача.

1) Правило 8 самое классное, да. Особенно на контестах вроде GCJ или FHC куча индусов оставляют код в публичном доступе во всяких git\ideone, скопипастил, заслал, прошёл на онсайт. Ну или квал не прошёл, как повезёт.

2) Модификация приёма 5, "Думайте вместе". Дайте задание своим двум сокомандникам думать над задачей, а сами тем временем попейте чаю или посидите с умным видом.

3) Приём "Подсмотреть-подслушать". Если у Вашей команды идей нет никаких по задачам, а рядом сидит команда из трёх красных и громко обсуждает решение задачи J, то стоит прислушаться к отцам и возможно "позаимствовать" их идею.

4) Приём "отсекай-упихивай". Напишите решение, которое работает за неполиномиальное время, например перебор, и путём нехитрых оптимизаций, упихиваний и огненных жертвоприношений Владыке Света затолкайте его.

Technique 2 appears to be unformatted on my browser. Anyway, thanks so much for this!

Thanks for the edit! :)

Auto comment: topic has been updated by MikeMirzayanov (previous revision, new revision, compare).

Thanks for editorial!

Когда решаешь задачу, бывает полезно поперебирать алгоритмы, которые ты знаешь. Можно посмотреть на ограничения. Например, если ограничение 10^5, то наверно решение работает за O(N * logN) и тогда стоит перебирать алгоритмы, которые работают за такую сложность (в нашем случае — это сортировка, бинпоиск для каждого элемента, кучи). Попробовать подставить каждый алгоритм в решение задачи. Один из них скорее всего верный.

Команды средней силы часто пользуются текущей таблицей результатов, чтобы определить метод решения. Умозаключения вида "если это говно сдало задачу G, значит там тупо жадник" частенько оказываются полезными для таких команд. Также, глянув на таблицу, в которой Burunduk1 не может с 10 попыток сдать E, можно понять, что куб там не упихивается.

you know you are at the right online judge when CEO himself makes time to write tutorials.<3 CF <3

" Google " is most helpful technique!

Here's another technique to find solution which I think isn't covered here. Assume that you already have generated some data or you've already solved a part of the problem. Now using those, can you solve the rest of the problem? If yes, then solve the first part now. It's kind of fast prototyping.

The Feynman Algorithm is another way to do it:

1. Write down the problem.
2. Think real hard.
3. Write down the solution.

Я бы добавил, что перед отправкой желательно протестировать задачу на крайних случаях или макстестах, если это возможно. Далеко за примерами ходить не приходится, задача 570В. Очевидно, что крайний случай n=1, m=1. Но из-за того, что многие не проверили у себя этот тест, по этой задаче было огромное количество взломов.

Can you please shed some more light on technique 4, preferably using examples? Also, one example of technique 2 that can really show the power of boiling down specific problem's solution into a general solution would make it great.

Есть старая книжка Д. Пойа "Как решать задачу". Там конечно про чисто математические задачи (и даже с упором на геометрические) но по-моему там много хороших идей которые можно перенести и на задачи из СП.

Do you know any examples for 3rd and 4th techniques ?

For the Technique 7, I wonder that in C++ using Code::Blocks, complier GCC, is there any way to pause the black window when we run a program, so that we can look the numbers we printed out?

I mean, if I print out all of the numbers I want to look, the numbers will be full of the black window and they will be quite hard to check. I want to check them step by step at different moments.

In Pascal, we can use readln;.

In Code::Blocks, I tried system("pause");, getchar();, but they didn't work.

Wonderful Tips and Techniques. Thanks a lot.

Thank you for these pieces of advice!