581A — Хипстер Вася
Первое ответное число (количество дней, которое Вася сможет быть одет по моде) это min(a, b), так как каждый из этих дней он будет надевать по одному красному и по одному синему носку.
После этого у него останутся либо только красные носки, либо только синие носки, либо не останется носков вовсе. Поэтому второе ответное число это max((a - min(a, b)) / 2, (b - min(a, b)) / 2).
Асимптотика решения — O(1).
581B — Элитные дома
Данная задача решается следующим образом. Пойдем по массиву справа налево и будем поддерживать в переменной maxH максимальную высоту дома, который мы уже рассмотрели. Тогда ответом для i-го дома будет число max(0, maxH + 1 - hi), где hi количество этажей в i-м доме.
Асимптотика решения — O(n), где n — количество домов.
581C — Развитие навыков
Данную задачу можно решать несколькими способами. Рассмотрим самый понятный способ, который укладывается в заданное время.
Отсортируем заданный массив следующим образом — из двух чисел левее должно стоять то, к которому нужно добавить меньше единиц улучшений, чтобы оно стало кратно 10. Обязательно добавлять хотя бы одну единицу энергии. Например, если исходный массив {45, 30, 87, 26}, то после сортировки он должен выглядеть следующим образом — {87, 26, 45, 30}.
Теперь проитерируемся по отсортированному массиву слева направо по i от 1 до n. Пусть cur = 10 - (aimod10). Если cur ≤ k, присвоим ai = ai + cur, а из k вычтем cur, иначе, если cur > k выйдем из цикла.
Следующим шагом проитерируемся по массиву аналогичным образом.
Осталось посчитать ответ ans — проитерируемся по массиву по i от 1 до n и присвоим ans = ans + (ai / 10).
Асимптотика решения — O(n * log(n)), где n количество заданных навыков героя.
581D — Три логотипа
Данная задача решается несколькими способами, рассмотрим один из них.
Для начала подсчитаем суммарную площадь s данных нам прямоугольников. Тогда сторона ответного квадрата это sqrt(s). Если sqrt(s) не целое число, выводим -1. Иначе сделаем следующее.
Переберем порядок, в котором будем добавлять заданные прямоугольники в квадрат (это можно сделать с помощью next_permutation()), а также для каждого порядка переберем будем ли мы переворачивать текущий прямоугольник на 90 градусов или нет (это можно сделать с помощью двоичных масок). Изначально на каждой итерации квадрат c, в который мы добавляем прямоугольники ничем не заполнен (пустой).
Для каждого из добавляемых прямоугольников сделаем следующее — найдем самую верхнюю левую свободную клетку free в квадрате c (напомним, что мы также перебираем, поворачиваем ли мы прямоугольник на 90 градусов или нет). Попытаемся наложить текущий прямоугольник в квадрат c, причем его левый верхний угол должен совпадать с клеткой free. Если текущий прямоугольник полностью помещается в квадрат c и не накладывается на уже занятую каким-то другим прямоугольником клетку, заполним соответствующие клетки в квадрате c нужной буквой.
Если после добавления всех трех прямоугольников не нарушилось ни одно из условий и весь квадрат c оказался заполненным мы нашли ответ — выводим квадрат c.
Если ответ не нашелся ни для одной перестановки прямоугольников — выводим -1.
Для произвольного количества прямоугольников k асимптотика решения — O(k! * 2k * s), где s — суммарная площадь заданных прямоугольников.
Также данная задача для 3 прямоугольников имеет решение с разбором случаев с асимптотикой O(s), где s — суммарная площадь заданных прямоугольников.
581E — Кодзиро и Furrari
Пусть f — стартовая позиция, а e — конечная. Для удобства реализации и дальнейших рассуждений добавим заправку в точке e типа 3.
Первое замечание: никогда нет смысла идти налево из стартовой точки ведь мы в ней уже стоит с полным баком лучшего бензина. Замечание верно и для любой заправки, в которой мы можем оказаться (если в оптимальном ответе мы должны пойти налево до некоторой заправки pv, то почему бы не выкинуть весь путь из pv в текущую заправку v и обратно и от этого ответ станет только лучше). Теперь поймем как нам следует действовать если мы находимся в некоторой заправке v.
Первый случай: на расстоянии не более чем s находится заправка в качеством бензина не хуже, чем в нашей (можно считать, что в момент старта мы находимся на заправке типа 3, но добавлять такую заправку нельзя). Зафиксируем ближайшую из них nv (ближайшую справа, так как мы уже поняли, что идти влево нет смысла). В этом случае дозаправимся так, чтобы возможно было доехать до nv. И поедем в nv.
Второй случай: из нас достижимы только заправки с худшим качеством. Заметим, что это возможно лишь в случае, если мы находимся в заправке типа 2 или 3. В случае заправки второго типа у нас нет никакого выбора кроме как заправиться на полную и поехать в самую последнюю достижимую вершину (то есть вершину на расстоянии не более чем s). Если же мы находимся в вершине типа 3, то нужно идти по возможности в самую дальнюю вершину типа 2, если же такой нет то идти в самую дальнюю типа 1. Эти рассуждения верны в силу того, что нам в первую очередь необходимо минимзировать бензин типа 1, а при равенстве типа — 2. Как можно дальше нужно идти потому, что бензин в нашей вершине строго лучше достижимых, а тип 2 нужно выбирать, поскольку если мы можем доехать до типа 1 и он находится правее заправки типа 2, то мы можем это сделать, проехав через заправку типа 2, возможно улучшив ответ.
Это основные рассуждения необходимые для решения задачи. Далее будем считать диманику на всех суффиксах i заправок — ответ на задачу если мы стартуем из заправки i с пустым баком. Переходы мы должны сделать, рассматривая описанные выше случаи. Для пересчета динамики в v нам нужно взять значение динамики в nv и сделать пересчет в зависимости от случая. Если случай 1, то нужно просто к соответствующему значению прибавить расстояние d от v к nv. Если это случай 2 и мы в заправке типа 2 нужно ко второму значению ответа прибавить s, а из первого вычесть s–d. Если это случай 2 и мы в заправке типа 3, то нужно из значения, определяемого типом заправки nv вычесть s–d.
Теперь, чтобы ответить на конкретный запрос стартовой позиции нужно найти первую завправку правее стартовой позиции, сделать один переход и взять уже посчитанное значение динамики (конечно, пересчитав это значение в соответствии с вышеописанным).
Сложность решения по времени: O(n logn) или O(n) в зависимости от того как искать позицию в списке заправок (первое в случае бинпоиска, второе в случае двух указателей). Сложность решения по памяти: O(n).
581F — Зубликанцы и мумократы
Пусть количество листьев дерева (вершин степени 1) равно c. По условию c четно. Если вершин всего 2, то ответ 1. Иначе в дереве есть вершина не лист, подвесим дерево за эту вершину.
Теперь будем считать 2 динамики. Первая z1[v][cnt][col] — наименьшее количество разноцветных ребер в поддереве с корнем в вершине v, если вершина v уже покрашена в цвет col (col равен 0 либо 1), а среди листьев поддерева вершины v должно быть ровно cnt вершин цвета 0. Если мы в листе, то это значение легко посчитать. Если мы не в листе посчитаем значение с помощью вспомогательной динамики z1[v][cnt][col]: = z2[s][cnt][col], где s — первый сын в списке смежности вершины v.
Вторая динамика z2[s][cnt][col] нам нужна для того, чтобы распределить cnt листьев цвета 0 среди поддеревьев сыновей вершины v. Для подсчета z2[s][cnt][col] переберем цвет сына s — ncol и количество листьев i цвета 0, которые будут располагаться в поддереве вершины s и пересчитаем значение следующим образом z2[s][cnt][col] = min(z2[s][cnt][col], z2[ns][cnt–a][col] + z1[s][a][ncol] + (ncol! = col)), где ns — следующий после s сын вершины v. Заметим, что не имеет смысла брать a больше, чем количество листьев в поддереве s, ну и тем более — больше количества вершин в поддереве sizes (поскольку у нас просто не хватит листьев для покраски).
Оценка сверху для такой динамики O(n3). Покажем, что в сумме решение будет работать за O(n2). Посчитаем количество переходов: 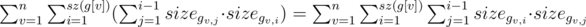 . Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n2).
. Заметим, что в последнюю сумму каждая пара вершин (x, y) войдет ровно один раз, именно при наименьшем общем предке v = lca(x, y). Таким образом переходов не более O(n2).
Сложность решения по времени и памяти: O(n2).











Thank you for fast editorial
Thanks for fast editorial :)
Wow you certainly came prepared with this! :) Thanks!
Such a fast system testing, thank you :D
problem C: what about if you have input
how you solve problem for much greater K where you need more then modulo 10
Answer is 20.
Because hero's skill can't be greater than 100, there is no need to use all K
For problem C it's easy to derive a O(n) solution if we consider sorting the numbers with a radix/bucket sort, as we only need to check the last digit.
C have solution O(n) 13267229
O(S) solution for problem D : https://ideone.com/HomOtB
Problems were very interesting. so good... thanks for making this contest!!!
What is test #5? Author, could you kindly share this test somewhere? It looks like random test, but my solution fails on it. (It seems it works fine for all small tests from your test set).
Мне всё понравилось, спасибо!
Can someone please explain the solution to F in more detail: I do not get how we are calculating z2[s][cnt][col] using information from the next child of s. How can we use a value in the DP table that is being computed in the same "level". As in won't z2[ns][ * ][ * ] be uncomputed when we are trying to calculate z2[s][cnt][col]?
You can calculate DP from the right to the left, from last child to the first. Also you can use "lazy DP" — if needed value is not calculated — calculate it recursively. Else just take calculated value.
I have a 20 line brute force solution for D that passed during contest which you may like: http://codeforces.me/contest/581/submission/13283931
Wow, very interesting solution. Congratulations on such a large rating increase ;)
This was a really interesting contest! Thanks for it :)
I have a question regarding the solution's time complexity for problem F, though, and if anybody could explain it in intuitive terms, I would be much obliged! (I don't really understand the last summation, I only understand that the first summation is 'for each node v', and the second summation is 'for each child i of node v')
Can somebody explain to me how works the DP solution of problem F? I didn't understand very well :/
PS: Very interesting contest :)
The overall idea of the dp is to try to color (starting from the root node) each node either 0 or 1, and to find the minimum number of 'bad' edges — edges which connect nodes of 2 different colors — within the subtree of that node, at the same time asserting that there must be a certain number of leaf nodes colored one color (in the editorial's case, 0).
The dp introduced in the editorial is termed like such: z1[v][cnt][col] (the first dp) which is the minimum number of bad edges in the subtree of v when v has col (0/1) for its color, and exactly cnt # of leaves in subtree of v are colored 0. So, the answer for the entire problem is min(z[root of tree][number of leaves / 2][0], z[root of tree][number of leaves / 2][1]).
Make sure you understand everything above before proceeding on because otherwise it might be difficult to understand the 2nd dp introduced in the editorial.
Now, how do you transition from z1[v][cnt][col] to another state? I.e. you have colored node v with color col, and you need to color cnt # of leaves with color 0. How do you proceed to color the nodes in the subtree to satisfy all these conditions? When you are z1[v][cnt][col], you have a list of children — call it C — of node v (say size m). You can color each of the children in C 0/1, but there is one condition that you must satisfy; for the transitions to the children in C, i.e. z1[C1][cnt1][0/1], z1[C2][cnt2][0/1], ..., z1[Cm][cntm][0/1], you must ensure that cnt1 + cnt2 + ... + cntm = cnt. You do this with the 2nd dp, that is a knapsack-style dp.
Now for the 2nd dp, it is termed like such: z2[s][cnt][col]. This one is complicated, so let me define some terms. p = parent of s. Define 'suffix subtree' of s to be the subtree of p excluding all the subtrees of the children of p which come before s in the child list of p and the edges that connect them to p. E.g. for a simple tree rooted at node 1, and 1 has children in its list C as 2, 3, 4, 5, in this order, then the 'suffix subtree' of node 3 will be the subtree of its parent, 1, excluding the subtree of 2 (because 2 is a child of 1 that comes in the list of children before 3) and the edge 1-2.
Now, with the terms above defined (and hopefully understood — especially the important idea of 'suffix subtree'), z2[s][cnt][col] is the minimum number of bad edges in the 'suffix subtree' of node s such that cnt # of leaves in the 'suffix subtree' are colored 0, and col is the color of parent p.
At this point, you should be able to understand why the transition for the first dp z1[v][cnt][col] is just the 2nd dp z2[s][cnt][col], where s is the first child of v.
Ok, so we have completely solved the first dp at this point, yay!
Finally, to finish off, we need to be able to solve the 2nd dp. How do we transit from z2[s][cnt][col]? Well, we know that we have to color s either 0/1, so try both colors (i.e. z1[s][ ][0] and z1[s][ ][1]) and take the minimum. So how do we know how many leaves in subtree of s we should color (I left blanks on purpose in above 'z1[s][ ][0] and z1[s][ ][1]')? Actually, we don't know. So, try all possibilities, i.e. z1[s][0...min(#leaves in subtree s, cnt)][0/1]. After putting i leaves in the subtree rooted at s, we have cnt-i leaves left to color, which we leave as a job for z2[ns][cnt-i][col], where ns is the child that comes directly after s in the list of children of p.
Hence the formula: (trying i from 0...min(#leaves in subtree s, cnt), and trying each color 0/1, called ncol) z2[s][cnt][col] = min(z1[s][i][ncol] + (ncol != col) + z2[ns][cnt-i][col]). Note that (ncol != col) is necessary because when the node s is colored differently from the parent node p, then p-s is a bad edge.
I have left out the base cases because I think you can figure that out yourself easily after you've understood the main bulk of the dp idea!
Hope I managed to help; I was quite confused at first, too! :)
Thanks for the brilliant explanation. Can you also explain why the dp is asymptotically order n^2 ?
Unfortunately I am still not able to understand the analysis in the editorial that proves it to be O(n^2) :(
...
One funny thing on F:
Even though the editorial specifically mentions the special case n=2:
"If in given graph only 2 vertices the answer is equal to 1"
there is no case with n=2 in the test data. You can be sure that quite a few wrong solutions pass in this way :P
Also just to add one thing:
You can do F with only one dp and without the extra parameter {0,1}. Think of it as coloring each node white or black. Then, can[x][j] is the minimum number of bad edges using the subtree of vertex x with exactly j dead zones colored black, where vertex x is colored white (almost...).
To do transitions we iterate over the children of vertex x and do it knapsack-style. In this setup, the number of bad edges is exactly the number of times we take a subtree rooted at a black node, which according to our earlier setup never happens (oops).
The fix here is to notice that we can flip an entire subtree, making the root black and inverting the colors of each dead ends within, so after calculating can[x], we apply the transitions can[x][s[x]-i]=min(can[x][s[x]-i],can[x][i]+1), where s[x] is the number of dead ends in x's subtree.
DO NOT see 13290307 for an implementation.
EDIT:
OK another weak thing about tests: O(n^3) solution without exploiting the property making it O(n^2) passes, for example my linked submission above. A countertest (like a long chain with a high-degree vertex at the end) is
Two fixes here:
Keep track of which values in cnt[x] are already filled in to be used, which reduces the complexity as desired, such as in 13291603.
Add size as you go (s[x] only includes already-processed children) — 13291744.
EDIT 2: Okay oops I'm dumb replace 5000 with 4999
F: where s — the first child int the adjacency list of vertex v. in ? :)
Here's my implementation to D problem. The same algorithm can be used to solve the problem with arbitrary k triangles. I hope this helps.
Can you share your code for problem E, for better understanding the idea ?
Thanks for the nice contest and solutions!
Насколько сложные эталонные решения C и D.
В С важен лишь остаток на 10. Считаем за линию сколько чисел во входе заканчиваются на 1-9. Жадным алгоритмом добавляем навыки сначала ко всем 9-кам (9, 19, ...,99) — там по 1 навыку надо, это дешевле всего. Потом к 8, там по 2, и т.д., потом к 1, там по 9. Добавляем пока не кончились свободные повышения. Если ещё остались, то добавляем количество навыков, делённое на 10. Если ответ больше чем 10n то делаем его равным 10n. Всё.
В D ясно что если решение есть, то самая длинная сторона самого длинного прямоугольника — это сторона квадрата. Дальше 2 случая. Либо у всех 3 прямоугольников равная длинная сторона, тогда располагаем их один под другим. получился квадрат — хорошо, нет — -1. Либо берём прямоугольник с самой длинной стороной, а два других располагаем под ним. Если этот самый длинный прямоугольник имеет размеры k*n, то два оставшихся должны иметь одну сторону равную n-k, а другие стороны в сумме давать n. Получилось — выводим, нет — -1. Всё.
+1 по обоим пунктам, так же делал. и в E динамика не нужна
Here is an alternate solution to E, which I think allows queries of pairs (f_i, e_i) rather than just f_i.
Let's think about the problem in this equivalent way:
We have a number line and several segments of length s labelled with 1, 2, or 3. We have queries of the form (f_i, e_i), meaning we want to go from f_i to e_i minimizing the time spent on first segments labelled 1, then segments labelled 2. We also begin with a free segment labelled 3 at f_i.
Here is how we answer one query:
First let f_i = f_i+s. The purpose of the free segment is to ensure it isn't better to first go backwards, but it's probably manageable without this restriction as well.
1: We check if it's possible at all — check if the entire length of the line between the two points is covered by some segment. If it isn't possible return (-1, -1), since there is some point we cannot pass.
2: If it is possible, we check how long we must spend on segments labelled 1. Convince yourself that this is simply the distance between the two points minus the length covered by only segments labelled 2 and 3.
3: We check how long we must spend on segments labelled 2. By similar reasoning, this is equal to the entire distance minus the length covered by segments labelled 3, minus the answer found in step 2.
To implement this for problem E, we use coordinate compression and prefix sums for what is covered by each set of numbers used above ({1,2,3}, {2,3}, {3}). The span between the query and the first compressed point must be dealt with as a special case.
Overall, it is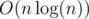 time (which can be made O(n) after sorting with two pointers) and O(n) memory. Here is my implementation: 13309041.
time (which can be made O(n) after sorting with two pointers) and O(n) memory. Here is my implementation: 13309041.
EDIT: You can also remove the special case by doing it offline: 13309187.
Hello :),
Did anyone implemented problem F according to the editorial?
I didn't understand the complexity analysis of the problem F.
Can someone explain it in detail?
.
.