А. Зеркальные числа.
Во-первых, заметим, что если интервал содержит число, состоящее из a цифр, а также число из b цифр (где a > b), то нет смысла рассматривать число из b цифр (так как вес числа 10^k больше весов чисел, меньших 10^k).
Если же рассмотреть числа с фиксированным числом цифр (s + 1), то для них сумма числа и его отражения — константа. Таким образом, учитывая что произведение чисел с фиксированной суммой растет при их сближении, картина у нас следующая: вес числа растет от 10^s до 5· 10^s -  1, затем он такой же у 5· 10^s, затем он убывает и достигает своего минимального значения в 10^s + 1 - 1.
Это доказательство, решение же такое: максимальный вес достигается либо в l, либо в r, либо в числах вида 5· 10^s (можно, например, проверить все s, такие, что 5· 10^s лежит в интервале).


B. И снова тетрис.
Легко видеть, что поле можно замостить фигурками всегда, когда на нем нет изолированных клеток.
Есть множество различных способов сделать это, мы приведем лишь некоторые из них.

1. Замощение доминошками.
Будем строить жадное паросочетание на клетках нашей фигуры объединяя их в доминошки. Идя слева-направо и сверху-вниз по нашей фигуре будем объединять все еще свободные пары соседних горизонтальных клеток, потом проделаем то же самое со все еще свободными клетками и вертикальными доминошками. Естественно, некоторые клетки не попали ни в какую из вертикальных или горизонтальных доминошек. Тем не менее, если клетка не была изолированной, то она прилегает к какой-нибудь из доминошек. Каждую из этих клеток можно отнести к любой из прилегающих к ним доминошек. Так как оставшиеся клетки не могут быть соседними и не могут прилегать к доминошкам слева (в силу порядка нашего обхода) все получающиеся фигурки будут состоять из не более 5 клеток.

Последнее, что осталось сделать — раскрасить наши фигурки указанным в условии образом. Это можно сделать, например так: раскрасим всю плоскость в 9 цветов, клетку (i ,j) в цвет (i % 3) * 3 + j % 3 (красим 3 × 3 в 9 цветов и замощаем им плоскость). Затем красим каждую доминошку в цвет ее черной (при шахматном раскрашивании) клетки. Каждую фигурку красим в цвет
доминошки вокруг которой она образована.

2. Жадность.
Будем снова пробегать массив содержащий поле слева-направо, сверху-вниз и жадно подбирать для каждой все еще свободной клетки фигурку. При этом будем выбирать ее так, чтобы никакая из свободных клеток, после этого не становилась изолированной. А именно будем докидывать к нашей фигуре каждую клетку, которая оказывается изолированной. Сделав это в правильном порядке получим фигурку из не более 5 клеток.

Красить фигурки можно прямо по ходу их образования. Будем просто поочередно выбирать цвет для каждой фигурки, проверяя какие из цветов уже заняты соседними раскрашенными фигурками и выбирая любой из оставшихся. Легко видеть, что 10 цветов хватит.


C. Генная инженерия.
Предположим, мы построили строку wp длины k < n и хотим узнать, сколько существует способов продолжить эту строку до строки длины n, удовлетворяющей условию фильтрации.
Какие параметры нам понадобятся, чтобы строить строку дальше?
Во-первых, нам необходимо знать, до какого места строка уже покрыта (обозначим этот индекс ci и назовем индексом покрытия). Кроме того, на необоходима какая-то информация о том, что находится на конце нашей строки.
Тут на помощь приходит довольно общеизвестная идея: найдем все префиксы ALL_P строк \{si\} и добавим к текущему состоянию следующий параметр: наибольший префикс 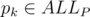, такой что wp оканчивается строкой p_k (в качестве альтернативы, можно рассматривать вершину бора, построенного по строкам из коллекции).
Теперь попробуем понять, почему этого достаточно. Во-первых, когда мы дописываем к wp какой-либо символ c мы можем легко найти p_k + 1. p_k + 1 будет равно наибольшей строке из ALL_P, такой, что p_k + c оканчивается на нее (мы можем предподсчитать все такие переходы заранее). Таким образом, единственная вещь, которую нам осталось научиться пересчитывать (чтобы использовать динамическое программирование) — это индекс покрытия. Но мы заметим, что он может измениться лишь какой-либо строкой коллекции, которая стоит на конце wp + c. Теперь заметим, что достаточно рассмотреть только самую длинную из таких строк (обозначим ее fs), и что fs обязательно содержится в p_k + 1 (и поэтому тоже легко предвычисляется для всех строк из ALL_P). Далее замечаем, что новый индекс покрытия зависит только он длины fs: он либо совпадает со старым, если fs не накрываем символ ci + 1, либо становится равным k + 1, если fs накрывает этот символ.

После вычисления всех величин d[k][k-индекс покрытия][макс. префикс] требуемое количество строк равно сумме d[n][0][mp] по всем префиксам mp.

D. Мощный массив.
Будем решать задачу оффлайн за время O(n sqrt(t)) и O(n) памяти. Для простоты рассуждений будем считать, что запросов n.

Пусть мы знаем ответ к задаче для какого-либо интервала и хотим узнать для другого. Будем двигать левый конец первого к левому концу второго, аналогично поступим с правыми концами. Сдвигая конец на один и поддерживая для каждого числа в массиве количество его вхождений в текущий интервал, мы сможет пересчитывать как нужную нам величину, так и поддерживать вхождения чисел за O(1). Назовем процедуру сдвига на один шагом.

Обход запросов в произвольном порядке, разумеется, обойдется нам в O(nt) шагов.
Пусть p = sqrt(n). Разобьем массив на p равных частей Q_1, ... Q_p. Теперь рассмотрим запросы вида (Q_i, Q_j) по всем i и j (их будет приблизительно n). Очевидно, никакой порядок обхода не даст нам количество шагов, меньшее O(n sqrt(n)), так как на переход от одного интервала к другому в
любом случае потребуется хотя бы sqrt(n) шагов.

Тем не менее, порядок обхода, гарантирующий O(n sqrt(n)) ходов в худшем случае, существует.
Отсортируем интервалы запросов по следующему правилу: сначала идут те, левый конец которых лежит в Q_1, затем те, левый конец которых лежит во Q_2 и так далее до Q_p. Если же левые концы запросов лежат в одной части, то раньше идет тот запрос, у которого правый конец меньше.

Проследим за шагами левых и правых концов при таком подходе. Левые концы в одной группе Q_i совершают <= n / p шагов, при переходе к Q_{i+1} <= 2 * n / p шагов. Поэтому всего левые концы совершают <= n / p * n + 2*n шагов (второе слагаемое порядка O(n), оно неинтересно).
Правые концы в одной группе движутся только вправо, это дает <= n * p шагов в ходе всего процесса, при переходе же к следующему Q_i грубо оценим переход n шагами, поэтому в итоге имеем <= 2 * n * p шагов.
Итого количество шагов <= n/p * n + 2 * n * p. Выбирая p, равное sqrt(n), получаем нужную асимптотику.

Решение: сортируем запросы по описанному правилу, затем в лоб переходим от одного запроса к другому в этом порядке.

Замечание 1. Никакой особенности, кроме неаддитивности, у функций из условия не было.

Замечание 2. В случае n, не равного t, получается оценка 2 * n * sqrt(t), и она точна (если внимательно проследить за доказательством, легко построить подпирающий оценку тест).

E. Длинная последовательность.

Для начала заметим, что есть только 49 вариантов входных данных.
Поэтому решения, которое предподсчитает все ответы за конечное время (даже если оно будет превышать лимит) будет вполне достаточно.

Для начала решим чуть более частную задачу. Предположим, что c₁, c₂, ..., c_k и a₀, a₁, ..., a_k - 1 нам уже даны и мы хотим проверить является ли последовательность {a_i} построенная по ним длинной. Если она периодична, то среди k-кортежей a_s, a_s + 1, ..., a_{s + k - 1} встречаются все ненулевые k-кортежи. Поэтому нет разницы с какого из них начинать последовательность. Поэтому свойство последовательности <<быть длинной>> зависит только от c_i, и a₀, a₁, ..., a_k - 1 мы можем выбрать любыми удобными. Будем теперь считать, что a₀, a₁, ..., a_k - 2 --- нули и a_k - 1 = 1.

Рассмотрим матрицу перехода A последовательности: при i < k ее i-ая строка равна (0, 0, ... 0, 1, 0, ..., 0), где 1 стоит на (i + 1)-ой позиции, а последняя строка равна (c_k, c_k - 1, ..., c₂, c₁).

Обозначим x_s вектор-столбец (a_s, a_s + 1, ..., a_{s + k - 1})^T.
Тогда для любого целого s: A· x_s = x_s + 1.
Последнее равенство это просто переформулировка рекуррентного соотношения:

a_n = c₁ * a_n - 1 + c₂ * a_n - 2 + ... + c_k * a_n - k.

Тогда, применяя A последовательно получаем: A^p· x_s = x_s + p для любого p ≥ 0. Таким образом p --- период тогда и только тогда, когда для всякого вектора x, появляющегося в нашей последовательности: A^p· x = x. Если последовательность не длинная, то априори не очевидно, что A^p единичная матрица, поскольку x принимает не все возможные значения. 

Но мы выбрали x₀ = (0, 0, ..., 0, 1), поэтому ясно, что вектора x₀, x₁, x₂, ..., x_k - 1 образуют базис. Отсюда если A^p· x_i = x_i для всякого i, то A^p --- единичная матрица.

Таким образом, нам достаточно сделать следующее:

1) Построить матрицу A по коэффициентам c_i.

2) Проверить, что A^2k - 1 --- единичная матрица. (Если нет, то 2^k - 1 не период.)
Если 2^k - 1 период, то нам осталось проверить, что он минимальный. Любой период делится на минимальный, поэтому нам надо проверить лишь делители 2^k - 1.

3) Построить все максимальные делители 2^k - 1 и проверить, что они не периоды (снова с помощью A).

(Под максимальным делителем n подразумевается делитель вида n/q, где q --- простое).

Все что нам осталось заметить, так это то, что такие последовательности всегда существуют. Более того, количество подходящих наборов c_i довольно велико. Можно показать, что их ровно 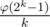(так как они соответствуют коэффициентам неприводимых множителей круговых многочленов над 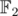). Поэтому можно просто брать произвольный набор и проверять его, достаточно скоро мы получим подходящий.