Codeforces Round #315 Editorial

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

569A - Music

Пусть перед очередным запуском прогружено S секунд песни, найдем, сколько будет прогружено перед следующим запуском. 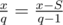$\text{[math]}$ . Отсюда x = qS.

Тогда решение: будем умножать S на q пока S < T. Количество таких умножений — это ответ.

Сложность — 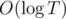$\text{[math]}$

569B - Inventory

Подойдём к задаче с другой стороны: а сколько максимально можно оставить номеров, чтобы получилась перестановка? Очевидно, что эти номера должны быть от 1 до n, причем среди них не должно быть повторяющихся. И понятно, что это условие необходимое и достаточное.

Такую задачу можно решать жадным алгоритмом. Если мы встретили число, которого ещё не было, при этом оно от 1 до n, то мы его оставим. Для реализации можно завести массив used, в котором отмечать уже использованные числа.

Затем нужно ещё раз пройти по массиву и распределить неиспользованные числа.

Сложность — O(n).

568A - Primes or Palindromes?

Известно, что количество простых чисел, не превосходящих n, — число порядка 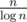$\text{[math]}$ .

Если мы зафиксируем длину числа k, то количество палиндромных чисел такой длины будет порядка 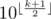$\text{[math]}$ . Это $\text{[math]}$ .

Таким образом, количество простых чисел асимптотически больше количества палиндромных чисел, а значит для любой константы A найдётся ответ. И для такого ответа 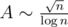$\text{[math]}$ . В нашем случае n будут не больше 10⁷.

Поэтому мы можем для всех чисел до 10⁷ проверить, являются ли они простыми (с помощью решета Эратосфена), а также являются ли они палиндромными (с помощью наивного алгоритма, или же можно динамикой считать зеркальное отображение числа). Затем мы посчитаем префиксные суммы, а потом линейным поиском найдём ответ.

При A ≤ 42 ответ не превышает 2·10⁶.

Сложность — 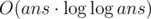$\text{[math]}$ .

568B - Symmetric and Transitive

Давайте сначала разберёмся, в чем же конкретно неправ Вовочка. В доказательстве хорошо всё, кроме того, что мы сразу взяли a, b такие, что 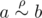$\text{[math]}$ . Если такие есть, то действительно 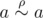$\text{[math]}$ . А если их нет? Если для a нет такого b, что 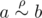$\text{[math]}$ , то, очевидно, не 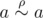$\text{[math]}$ (иначе мы бы взяли b = a).

Отсюда понятно, что наше бинарное отношение — это какое-то отношение эквивалентности, к которому присоединили такие элементы a, что для всех них не существует таких b, что 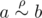$\text{[math]}$ .

Тогда решение можно разбить на две части:

Посчитать количество отношений эквивалентности на множествах размеров 0, 1, ..., n - 1
Посчитать, сколькими способами туда можно добавить недостающие "пустые" элементы.

Отношение эквивалентности можно задать разбиением на классы эквивалентности.

Тогда первую часть задачи можно решить динамическим программированием: dp[elems][classes] — кол-во способов разбить elems первых элементов на classes классов эквивалентности. Переход — каждый элемент мы можем либо отнести в один из уже существующих классов, тогда их количество не изменится, либо же создать новый класс, тогда их количество увеличится на 1.

Вторая часть задачи. Зафиксируем m — размер множества, над которым мы посчитали количество отношений эквивалентности. Тогда нам нужно добавить к нему ещё n - m "пустых" элементов. Позиции для них можно выбрать C[n][n - m] способами, где C[n][k] — биномиальные коэффициенты. Их можно заранее посчитать треугольником Паскаля.

Тогда ответ — $\text{[math]}$ .

Сложность — O(n²)

568C - New Language

Пусть мы зафиксировали буквы на каких-то позициях, как проверить, что на остальные позиции можно расставить буквы так, чтобы получилось слово из языка? Ответ — 2-SAT. Действительно, для каждой позиции есть два взаимоисключающих варианта (гласная и согласная), а правила языка — это импликации. Таким образом, такую проверку мы можем сделать за O(n + m).

Будем уменьшать длину префикса, который мы оставляем таким же, как у слова s. Тогда следующая буква должна быть строго больше, чем в s, а весь дальнейший суффикс может быть любым. Переберём эту букву и проверим с помощью 2-SAT, есть ли решения. Как только мы обнаружили, что решения есть, мы нашли правильный префикс лексиграфически минимального ответа. Затем будем обратно наращивать префикс, какая-то из букв точно подойдёт. Мы получили решение за O(nmΣ ). Σ из решения можно убрать, заметив, что каждый раз нам нужно проверять только минимальные подходящие гласную и согласную буквы.

Также нужно не забыть случай, когда все буквы в языке одной гласности.

Сложность — O(nm)

568D - Sign Posts

Предположим, что решение есть. Если n ≤ k, то мы можем на каждую дорогу поставить по столбу. Иначе рассмотрим любые k + 1 дорогу. По принципу Дирихле среди них найдутся две, для которых будет общий указатель. Переберём эту пару дорог, поставим столб на их пересечение, уберем дороги, которые тоже проходят через эту точку. Мы свели задачу к меньшему числу столбов. Таким рекурсивным перебором мы решим задачу (если решение существует).

Решение это работает за 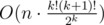$\text{[math]}$ . Если написать аккуратно, это может зайти.

Но это решение можно ускорить. Заметим, что если у нас есть точка, через которую проходит хотя бы k + 1 дорога, то мы обязаны поставить столб в эту точку. При достаточно больших n (у меня в решении отсечка n > 30k²) такая точка точно есть (если решение существует), причём её можно искать вероятностным алгоритмом. При условии, что решение существует, вероятность, что две произвольные дороги пересекаются в такой точке не меньше 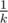$\text{[math]}$ , поэтому если попробовать 100 раз, то с вероятностью 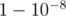$\text{[math]}$ такая точка найдется, и мы сможем уменьшить k.

Все проверки можно делать в целых числах.

Сложность — 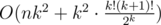$\text{[math]}$ .

568E - Longest Increasing Subsequence

Будем поддерживать массив c: c[len] — минимальное число, на которое может заканчиваться возрастающая подпоследовательность длины len (Одно из двух стандартных решений задачи о наибольшей возрастающей подпоследовательности). Элементы этого массива возрастают и добавление очередного элемента v к обработанной части последовательности сводится к нахождению такого i, что c[i] ≤ v и c[i + 1] ≥ v. При обработке пропуска нам нужно попробовать вставить все числа из множества b. Предварительно их отсортировав и двигаясь двумя указателями вдоль массивов b и c мы можем проделать нужные обновления за O(n + m).

Авторами подразумевалось использование O(n) памяти для восстановления ответа. Этого можно добиться следующим образом: 1. Параллельно с массивом c будем хранить массив c_index[len] — индекс элемента, на который заканчивается оптимальная НВП длины len. Если она заканчивается в пропуске — будем хранить, например, - 1. 2. Также сохраним для каждого не пропуска — длину НВП(lenLIS[pos]), заканчивающейся в этой позиции (это несложно делается в процессе вычисления массива c) и позицию(prevIndex[pos]) предыдущего элемента в этой НВП (если это пропуск, опять же - 1).

Теперь приступим к восстановлению ответа. Пока мы не наткнулись на пропуск — можно спокойно восстанавливать НВП с конца. Сложность обнаруживается, когда несколько следующих элементов последовательности попали в пропуски. Но можно несложно определить что это за пропуски и чем их заполнить. А именно: пусть сейчас мы стоим в позиции r. Нам нужно найти такую позицию l (не пропуск), что мы сможем заполнить ровно lenLIS[r] - lenLIS[l] пропусков между l и r возрастающими числами в интервале (a[l]..a[r]). Позицию l можно итеративно перебирать от r - 1 до 0, параллельно насчитывая число пройденных пропусков. Проверку условия описанного выше можно несложно сделать с помощью пары бинпоисков.

Немного подробнее и с деталями:

Как узнать, что между позициями l и r можно заполнить пропуски так, чтобы не ухудшить генерируемый ответ?
Пусть countSkip(l, r) — количество пропусков на интервале (l..r), а countBetween(x, y) — количество различных чисел из множества b, лежaщих в интервале (x..y). Тогда позиции l и r хорошие тогда и только тогда, когда lenLIS[r] - lenLIS[l] = min(countSkip(l, r), countBetween(a[l], a[r])). countSkip можно насчитывать в процессе уменьшения границы l, countBetween(x, y) = max(0, lower_bound(b, y) - upper_bound(b, x)).
Что делать, если НВП заканчивается или начинается в пропуске (тогда мы не знаем, откуда начать/где закончить)?
Наиболее простым решением будет добавить - ∞ и + ∞ в начало и конец нашего массива соответственно. Это позволит избежать проблем с такими крайними случаями.

Сложность — 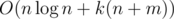$\text{[math]}$ времени, O(n + m) памяти

Комментарии (83)

Показать архивные | Написать комментарий?

Um_nik

9 лет назад, # |

Auto comment: topic has been translated by Um_nik(original revision, translated revision, compare)

→ Ответить

Frez

+17

thanks for fast editorial :)

CMaster

-9

Будет ли авторские решении?

m.khooryani

-42

"Music", worst problem I've ever seen!

kalimm

9 лет назад, # ^ |

+10

"Misic", wirst priblim I'vi ivir siin.

-19

kisi bibit

bichi kiini

shamir0xe

البته باید با ننش کار می‌داشتی :))

بله حق با شماست

هرچی بگی کمشه

:))

Bat-Orgil

-34

Fast Editorial

bicsi

For problem 568B — Symmetric and Transitive I propose an alternate view:

Let's suppose we see the relation as a graph. In essence, a-R->b will mean the edge (a,b) in our graph. Now, the properties translate to:

(u, v), (v, w) exist => (u, w) exists (transitivity) The graph is undirected (symetry) There is (u, u) for each u (reflexivity).

Now, we notice some properties: - (u, v) exists => (v, u) exists => (u, u) exists (by reflexivity and transitivity). - also by transivity, we can see that each vertice of a graph is either isolated (has no incident edges) or is part of a clique — this is important.

So, the graph is a reunion of cliques of size >= 1 plus a number of isolated vertices. Now, let's suppose that k vertices are isolated. Then n-k of them are part of the "reunion of cliques". Now, we can choose the k isolated vertices in (n choose k) ways. The rest is a reunion of cliques. Simply, every node is part of a clique (of size >= 1).

If we consider Cliques[i] -> the number of graphs that are "reunion of cliques" with i vertices, then the answer is sum(1, n-1) (n choose k) * Cliques[n-k] + 1. The "1" represents an empty graph, which was not considered earlier.

To calculate Cliques[i], we can think of every node taking part of a clique. It's easy to see why this relates to partitions. In particular, Cliques[i] is the total number of ways to partition i numbers. It is equal to S[i][1] + S[i][2] + ... + S[i][i], where S[i][j] is the 2nd Stirling's Number (i.e., the number of ways we can partition i items in j groups).

So, basically, we calculate S[i][j](Stirling), C[i][j](Combinations), and then Cliques[i] (as S[i][1] + S[i][2] + ... + S[i][i]). Now, the answer is C[n][1] * Cliques[n-1] (1 isolated node) + C[n][2] * Cliques[n-2] (2 isolated nodes) + ... + C[n][n-1] * Cliques[1] (n-1 isolated nodes) + 1 (empty graph). I hope it was clear enough, I don't know how to write explanations that well :)

AnonymousBunny

← Rev. 9 →

+24

I used a different dp for computing the number of equivalence relations on a set of size n in 1B/2D: let dp[i] be the number of equivalence relations on a set of size i. While computing dp[i+1], consider a particular number (say i+1)- let's say there are x other elements belonging to the equivalence class of that number. Once we select those x numbers (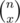 $\text{[math]}$ ways to do that), we have dp[i-x] possibilities for the remaining numbers, giving the recursion

$\text{[math]}$

sunkuet02

Please explain "For A ≤ 42 answer is smaller than 2*10^6." for 569C - Простые или палиндромы?

What don't you understand? It is statement about maximal answer, it is true.

I ain't understand that why it is less than 2*10^6 ? My code have failed, because I have used until 10^7.

(Sorry for my bad English)

We have proved that it is less than 10^7 and then found real answer.

I can't understand your question.

Sorry for my misconception. Thanks .

MiniFake

← Rev. 3 →

In your code:

if(q*cntprime[i] <= p*cntpal[i]){
            cout << i << endl;
            return 0;
}

q*cntprime[i] and p*cntpal[i] can be >= 2^32 but you used type int it makes overflow.

evenharder

I guess the doubt of sunkuet02 originates from the fact that there is no strong mathematical proof with the upper bound in this logic. Although we, the competitive programmers often think like 'Accepted = Correct Logic'. Honestly, I also set the upper bound as 2 * 10⁶ with vague guess(with the prime number theorem), hoping that there won't be any countercases.

Strong mathematical proof was used to proof the 10⁷ bound.

numbertheorist17

+14

See, the actual proof gives the bound of 10⁷. You can actually run the program with 10⁷ on your computer during the contest to make the bound to be 2·10⁶ which is much better.

baal-hammon

I really don't inderstand why n<10^7

Can anyone explain it rigorously ??

balalaika

I don't understand logic of editorial too, but I understood for n>40 pi(n)/rub(n) > pi(n-1)/rub(n-1). Then with brute-force found for A = 42 answer is 1179858.

It isn't true.

Oooopss.... My bad. Looks like my proof of that was wrong.

Swistakk

← Rev. 4 →

+57

Using randomization in D is really unreasonable. Assume n is high and take just first 26 lines. We can check all O(26^2) intersections and if there is no such one that it has at least 6 lines passing through it we can answer NO, and if there is one, we need to take it and proceed recursively.

After that phase we can assume that n<=25 and k<=5, what we need to do here is a creative bruteforce, I used an observation that we need to take at least one point which has at least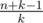 $\text{[math]}$ lines passing through it. Another important observation is that if we consider two sets of lines passing through common point then they have at most 1 lince in common, so there can't be many points having many lines passing through it (if n=25 there won't be more than ~7 of them), so that's the point where I used my common sense which told me that branching over "big" points will be sufficient.

Btw, what I'm pretty proud of is that I managed to use one code for both parts (http://codeforces.me/contest/568/submission/12452255) :P

It's great, thank you for your solution!

dj3500

FWIW, what you did in the first phase is called kernelization :) Too bad I didn't read the problem, it's quite nice.

aaaaajack

Wow, great solution!

geniucos

I have a question about your solution. Somewhere there, when you've just found a point which is on at least min_sz lines(of course min_sz from the first, on your example, 26 lines, in general from the first K ^ 2 + 1 lines) you have 2 cases. In the case when you have N > K ^ 2 you directly return the recursive result, but there may be some other ways to get a solution(if this way returns 0, than everything will be 0, but you didn't even try some other way to choose a point which is on at least K + 1 lines). So my question is, in case of N > K ^ 2, why do you stop the recursivity at the first point which meets the condition?

If I have n > k^2 then min_sz = k + 1 and if this point won't be taken into solution then since those k+1 lines don't have anything in common but this point I will need to use at least k+1 points to cover those lines, which is too much. Because of that I'm 100% sure that if solution exists then it has to contain that point, so I can directly return result of recursive call here.

Thanks a lot. I understood it. That's an awesome solution :)

kingofnumbers

← Rev. 2 →

Could explain how did you compute complexity of recursive solution of Div1 D?

UPD: ok because it's O(N * C(2,2) * C(3,2) .. * C(K,2) )

We should try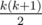 $\text{[math]}$ variants for fixed k. To mark used lines we spend O(n) time.

Product of this fractions is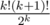 $\text{[math]}$

Complexity —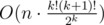 $\text{[math]}$

PLUkraine

Can someone explain how to solve div 2 A? I didn't get it from this editorial. What is x?

mohammad74

← Rev. 5 →

x is downloaded seconds of music when we must replay music again.

speed of downloding music seconds = q-1

speed of listening to music = q reachtime = the time that will spend from the moment that we play music for the first time until we reach download limit.

This "reachtime" for both actions "downloading" and "listening" must be equal. So we will calculate "reachtime" for both actoins.

reachtime for listening = x/q (why? because: (downloaded amount)/(speed) is equal to time (eg. distance/speed=time)).

reachtime for downloading = (x-s)/q (!when we play music for the first time we have downloaded s seconds of music and must download (x-s) seconds more)

and now:

reachtime for listening = reachtime for downloading

x/q = (x-s)/(q-1)

after solving above equation:

x=qs

Another approach for 568B - Симметричное и транзитивное:

Let B_n be the number of ways that a set on n elements has an equivalence relation. It is known that a relation R is an equivalence relation on {1, 2, ..., n} if and only if it partitions the set. Therefore, B_n counts the number of ways to partition the set {1, 2, ..., n}.

Now, let C_n be the number of binary relations on {1, 2, ..., n} that are symmetric and transitive but not reflexive. The number C_n is what we are looking for. Note that for any binary relation counted by C_n, there is a set of elements that are partitioned already and a set of elements that are not in any part of the partition.

I claim that B_n + C_n = B_n + 1. This will be established by a bijection. Take any partition of {1, 2, .., n} and add the set {n + 1} to it. This will create a partition of size n + 1. Now for anything counted in C_n, take all the elements that are not in a partition yet and put them together in a set with n + 1 and this will create a partition for n + 1. This is easily seen to be a bijection.

Thus, the answer is C_n = B_n + 1 - B_n. Fortunately, B_n is a really well know sequence called Bell numbers: https://en.wikipedia.org/wiki/Bell_number. The relation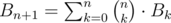 $\text{[math]}$ helps compute B_n in O(n²) time and O(n) memory. Then it is easy to compute C_n.

jzh

Dang you are a cool guy

lnishan

Now for anything counted in C_n, take all the elements that are not in a partition yet and put them together in a set with n + 1

I love the idea here :)
Also thank you for pointing us to Bell numbers (I love combinatorics!).
It took me a day (not in a good health condition atm, feeling stupid) to grasp all these.

yaksha

7 лет назад, # ^ |

-20

sorry for necroposting but I love you.

Sammarize

+16

Очень хороший разбор, спасибо

xyz222

+19

I think this code is really easier to understand than this big editorial for B div1.

The idea is a dp that iterates over all i < n, and put it on a existent group, ignore it or create a new group with this i. The third parameter only says if already ignore some i.

Wow, man, that's impressive :)! I have though that mine code is clever, but you definitely beat it :). Even any binomial coefficients!

duckladydinh

{ You code is great. I understand your code but I just don't understand what it is that the problem requires us to do. ( Sorry but the problem statement looks confusing to me :'( }

gupta_shvm

Can someone explain what this means from Div1 B, in a simpler way, or with pseudocode?:

So first part can be solved using dynamic programming: dp[elems][classes] — the numbers of ways to divide first elems elements to classes equivalence classes. When we handle next element we can send it to one of the existing equivalence classes or we can create new class.

waterfalls

+23

One slight hole in the test data for div 1 C — solutions that just use a "topological" sort of the entire implication graph rather than of the SCC-condensed graph still pass: 12459610

Example test breaking my above solution (uses some things specific to my implementation, and almost all AC submissions during contest pass it):

CV
6 9
1 C 2 C
1 C 2 V
3 C 5 V
5 V 4 C
4 C 3 C
3 C 6 C
6 C 3 V
6 C 5 V
6 C 4 C
aaaaaa

innok96

Poblem div1 B. Can you explain me why in test 4 answer is 37

jugal_sahu

Can anyone please tell me what we have to do in problem "Symmetric and Transitive" i didn't get? please explain.. :(

What is 2-SAT ? please explain or give some useful links...?

https://en.wikipedia.org/wiki/2-satisfiability

Can't you google "2-SAT" yourself?

uttom

Problem:DIV2 C In editorial The number of palindrome O(sqrt(n)) but when n=10 then the number of palindrome is=9 but sqrt(10)=3.16 i found mismatch .. Please explain it ..

Don't you familiar with big-O notation?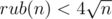 $\text{[math]}$

I know it,but i could not think in that way.. thanks

No_mercy_

Div1 B. Can you please name relations when n = 3?

1) empty

2) (x x)

3) (y y)

4) (z z)

5) (x x); (y y)

6) (x x); (z z)

7) (y y); (z z)

8) (x x); (x y); (y x); (y y)

9) (x x); (x z); (z x); (z z)

10) (y y); (y z); (z y); (z z)

P.S. I have a question: how to write a new line (I use Shift + Enter and get empty lines between maybe there is alternative way)?

You can print two space after the line
like this

Thanks!

Thank you!

SomeRandomGuy

<Br>

pyrexshorts

Sorry, this is a bit late, but I'm not sure why set #8 is not reflexive, since it contains (x, x) and (y, y).

rkanine

8 лет назад, # ^ |

but it doesn't contain (z,z)....since n=3 for the relation to be reflexive it must contain (i,i) for all i from 1 to n

+11

Рихаил Мубинчик

Ofegenia

Problem 569A has a shorter solution. Because sequence {x_n} is geometric progression with ratio q, x_n = S·qⁿ > = T. Thus,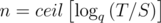 $\text{[math]}$ .

chemthan

Yes, that is correct formula. But computing directly the formula can get WA.

Isn't there a paradox in div2 A? For example, if it takes t time to listen to the x seconds downloaded, then when t is reached, some seconds of the song has been downloaded in that time. Then this repeats over and over again, so that you can never really reach the end of the song?

Zeno's paradoxes
No, there isn't.

dush1729

Infinite Geometric progression with common ratio less than 1.

Guliash

А для того, чтобы решить 2sat с частично заданными аргументами, то необходимо для этих аргументов добавить условия: (x_i||x_i), если x_i = true, и (!x_i||!x_i) для x_i = false?

suraj021

Problem C Div2:"Then we can calculate prefix sums (π(n) and rub(n)) and find the answer using linear search." What is Prefix sums in the statement?

Bera

Prefix sums : ith number keeps the sum of 1-i.

limed

FWIW: solved Div1C without any 2SAT: 12578725 Unfortunately, not during the contest:)
Precomputed all possible implications transitively from the given ones (O(n^3), Floyd-Warshall like). Then used them to check feasibility of a fixed prefix in O(n^2). Overall complexity — O(n^3), which is the same as given in the editorial (O(nm)), but IMHO the logics is somewhat simpler.

Can someone help me? I tried solving div1E problem and I'm getting Time Limit exceeded: http://codeforces.me/contest/568/submission/12902289 What's strange is that function Read () is getting TLE alone...I really don't understand why it is moving so slow. All it does is to read the input and sort vector B :(. Thanks in advance

Megumi233

Problem div1D, I have a question that why the probability of the two arbitrary roads are intersects in such a point is at least 1/k

+18

There is also a hole in the test data for div 1 D:

I thought this was a really nice problem when solving in practice, kudos to authors. Unfortunately my solution back then was wrong :(

Some people (me) thought that if a point goes through at least N / K points, then it must be in any good configuration. Some other people thought that any point with a maximum number of lines through it is in any good configuration. Both of these statements are false. For example, consider

N=4, K=2

test

The red point has both N / K lines and a maximum number of lines through it. However, if we use this red point, we cannot find a solution. Of course, there is a solution, demonstrated by the green points.

Mine (12458083) fails on

4 2
1 0 2 (point 1)
-1 1 100 (point 2)
1 0 1 (point 3)
1 1 100 (point 4)

By rearranging the points (to account for randomness), 12453450 fails on 2413 and 12448661 fails on 1324.

Of course, it is rather hard to catch such bugs, since for this test we would need 6 tests, one for each choice of the first two points. Also, some people did the same thing with multiple iterations (12453811) which is probably almost impossible to break, so there is an alternate solution to be found here.

sithope

The solution of 568D is helpful for me.

miguelmaurizio

In problem D-div 1, could anyone explain me why if a point belongs to at least k + 1 roads it must be in the solution? Thank you!

I did Div2 A by Geometric progression ( Complexity -> O ( 1 ) )

Code

We have S seconds of song available and q seconds of playback gives ( q — 1 ) seconds of download. So for S seconds we will have S * ( q — 1 ) / q more download. For S * ( q — 1 ) / q seconds we will have S * ( q — 1 ) * ( q — 1 ) / ( q * q ) more download and so on. This will go till infinity and total sum of these values will give total time music played until music stops because of incomplete download. This is geometric series where first term is S and common ratio is ( q — 1 ) / q. So sum will be S / ( 1 — ( ( q — 1 ) / q ) ) which is equal to S * q.

So for S seconds of download we can listen till S * q seconds and then we will have to restart. Now we will have S * q seconds of download for which we can listen upto S * q * q seconds. This will go until it is greater than or equal to T. So we will have something like S * q * q * q . . . * q = T. Answer is number of times q.

Number of times q = log ( T / S ) to the base q.

Reckt

wonderful solution ! and well-explained.

markysha

Maybe i'm wrong, but why logl( X ) where X is some number works in O(1).

So I think your solution works in O(log(t) + log(q)).

animeshf

I can't understand the solution to Div 1B.

We're trying to compute the number of equivalence relations in a set of size x.
How does this transform into a "partition x numbers into g groups" dp?
What does a group/equivalence_class actually denote?
Could someone please elaborate?

ankeshgupta007

check this http://math.stackexchange.com/questions/676519/how-many-equivalence-relations-on-a-set-with-4-elements

An equivalence relation divides the underlying set into equivalence classes. The equivalence classes determine the relation, and the relation determines the equivalence classes.

I don't understand how an equivalence relation divides the set into equivalence classes :(
Can someone elaborate on this? (Sorry for such n00b questions)

Блог пользователя Um_nik