How to solve this Recurrence equations using matrix exponentiation for large n (n < 109) with modulo 106 :
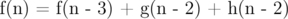


With base cases as 
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
How to solve this Recurrence equations using matrix exponentiation for large n (n < 109) with modulo 106 :
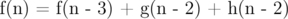


With base cases as 
| Name |
|---|



For any n you have vector having values for f(n),..,f(n-2),g(n),..,g(n-2),h(n),..,h(n-2) in some order, Then just make a matrix s.t. you get the right vector for n+1 when multiplying that vector from the left with that matrix.
Thank you adamant, Can you tell me what could be the possible values for 2nd matrix ?
What do you mean?
There's one nice trick. Notice 2nd & 3rd equations. Let p(n)=g(n)-h(n):
g(n)=f(n-2)+h(n-1), h(n)=f(n-2)+g(n-1)
Let's subtract: g(n)-h(n)=h(n-1)-g(n-1) => p(n)=-p(n-1) But g(0)=h(0) => p(0)=0. So, p(n)=0 for every n. It wields that g(n)=h(n). So, original system can be rewritten as following:
f(n)=f(n-3)+2g(n-2), g(n)=f(n-2)+g(n-1)
From here it can be easily shown that both of them satisfy the same equation: x(n)=x(n-1)+x(n-3)+x(n-4). Only initial conditions differ. If x=f, then x(0)=x(1)=x(2)=1. If x=g=h, then x(k)=k for k=0,1,2. So, you need only one matrix of order 4 to solve it. By the way, for x=f it's known sequence: OEIS.
Of course, it makes no sense because there is a simple solution as adamant shows =) But I think it's sometimes interesting to understand what's going on behind the scene.
Well, if this problem were on SPOJ it could be that your solution passes and mine not because of TL :)