Given x and y, we need to find smallest a and b such that
a + b = x
a xor b = y
How to solve this?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Given x and y, we need to find smallest a and b such that
a + b = x
a xor b = y
How to solve this?
How to calculate the fibonacci entry point for N numbers p1, p2, p3, ...., pn. (1 < = pi < = 109)
FEP(pi) = j such that jth fibonacci number is the first fibonacci number Fj divisible by pi
How can we find it efficiently for N numbers.
Ex,
input = 2, output = 3
input = 5, output = 5
input = 13, output = 7
Plane division by a common shape is a very well known topic of computer science. The pictures below shows some such diagrams. In figure 1 we find that four circles divide a plane in maximum 14 zones, four ellipses divide a plane in maximum 26 zones and three triangles divide a plane in maximum 20 zones. It is a common practice to find out the maximum number of regions when m shapes of same type intersects. For example the general formula for circles is m2 - m + 2. When the situation is hybrid (More than one type of shapes intersect) the maximum possible number of regions is also not very difficult to find out.
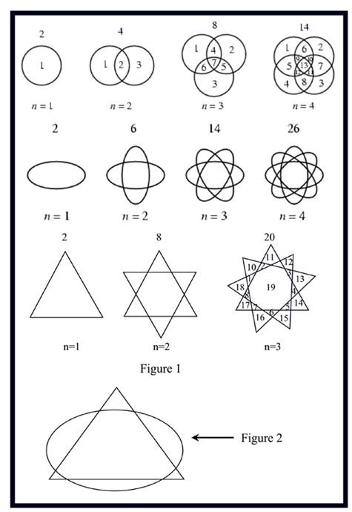
In figure 2 we can see that eight regions are created when one ellipse and one triangle intersect. In this problem you will have to think in the reverse direction. You will be given the maximum number of regions created and you will have to find how many ellipses, circles and triangles were involved.
Input
The input file contains less than 300 lines of inputs. Each line contains a 32-bit unsigned integer N, which is the maximum number of regions, created by m ellipses, n circles and p triangles. Input is terminated by a line, which contains a –1. This line should not be processed. All input numbers other than the –1 in the last line are positive numbers.
Output
For each line of input you have to produce two or more lines of output. The description of output for each line is given below:
The first line is the serial number of output. Each of the next lines contains three integers. These three integers are possible values of m, n and p for which maximum N regions is created. When there is more than one solution then the solutions should be sorted in ascending of m and then by ascending order of n. If there is no valid solution output a line “Impossible.” instead. Look at the output for sample input for details. Please note that for a valid solution 0 ≤ m < 100, 0 ≤ n < 20000 and 0 ≤ p < 100.
Input Ex
20
10
-1
Output Ex
Case 1:
0 0 3
0 1 2
1 0 2
1 3 0
Case 2:
Impossible.
How to solve this Recurrence equations using matrix exponentiation for large n (n < 109) with modulo 106 :
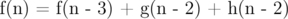


With base cases as 
In how many ways can you tile a 2 * n rectangle with triominoes? A triomino is a geometric shape made from three squares joined along complete edges. There are only two possible triominoes:
For example, you can tile a 2 * 3 rectangle only in 3 different ways. As the answer can be quite big, you just need to find the number of ways modulo 106.
Constraints : Number of test cases t (1≤t≤100). Each of the following t lines contains the value of n(0 < n < 109).
Output : Answer modulo 106.
How to count numbers whose binary representation has number of 1's multiple of 3 for all numbers between 1 to N.
For ex — N = 19 then ans = 5 Since, 7, 11, 13, 14, 19 have number of 1's multiple of 3.
Constraint : n < 1016
We call a natural number supernatural if it does not contain any ones in its decimal representation and the product of its digits is equal to n. For given n, find how many supernatural numbers exist.
Constraint : The input contains a single integer n not exceeding 2×109.
Output modulo 101.
I got this problem on link
UPD : I solved this problem but only 80% test cases are passing, rest giving TLE, can anyone please suggest how can i improve the below code using some trick or memoization:
#include<bits/stdc++.h>
using namespace std;
#define MOD 101
#define LL long long
#define out(x) cout << #x << " : " << x << "\n";
bool isPrime(LL n) {
for(LL i = 2;i * i <= n; i++) {
if(n % i == 0) return false;
}
return true;
}
LL ans = 0;
void solve(LL n) {
if(n <= 1) return;
if(isPrime(n)) {
if(n < 10) ans = (ans + 1) % MOD;
return;
}
if(n < 10) ans = (ans + 1) % MOD;
for(int i = 2;i < 10;i++) {
if(n % i == 0)
solve(n / i);
}
}
int main() {
ios_base::sync_with_stdio(false); cin.tie(NULL);
LL n; cin >> n;
solve(n);
cout << ans << endl;
return 0;
}
For two given integers n and k, How to find
(Zn + Zn - 1 - 2Zn - 2) mod 10000007,
where Zn = Sn + Pn and
Sn = 1k + 2k + 3k + ….. + nk and
Pn = 11 + 22 + 33 + …… + nn
Constraint : (1 < n < 2 * 108, 0 < k < 106)
I got this problem on link
Given the area of 3 triangles S1, S2 and S3 as shown in figure. 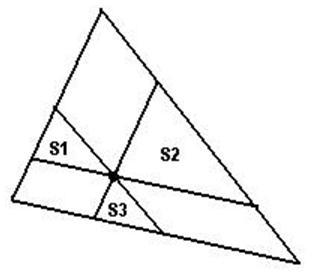
How to find the area of large triangle. ?
For example — if areas given are S1 = 1.0, S2 = 2.0 AND S3 = 3.0
Then Area of large Triangle = 17.19150823
I got this problem on link
Given value of n, how can we find the power(p) of 2 such that the result 2^p starts with n.
For ex —
n = 12 then answer is 7 i.e., 2^7 = 128.
n = 82 then answer is 209 i.e., 2^209 = 822752278660603021.........
If no such power exist then p should be -1.
I have coded it, but giving WA and TLE on some test cases. Here is the link to my code : link
How can we find power efficiently ? I got this problem on link
UPD : Thank you all, Temirlan's approach helps me to get AC. In case anyone interested, here is the link to my code : link
| Name |
|---|


