Сегодня в 17:00 по Москве начинается третий раунд Google Code Jam, топ-25 участников которого отправятся на финал соревнования в Сиэтл. Всем удачи!
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:39:38
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:39:38
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 05:55:23 (k3).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Auto comment: topic has been translated by Zlobober(original revision, translated revision, compare)
is tourist or Petr Participate?
is tourist or Petr Participate?
No . Tourist was the winner of Code Jam 2014, so he got a direct entry to this year's final .
tourist is Participating!
TankEngineer missed by just 15 seconds
At least two teenagers (me and jcvb) are in top 25. And champion(tourist) in the last year. I'm not sure whether ecnerwala and JoeyWheeler are adults. So I think people ranked 26, 27 and 28 will advance.
He will advance because tourist is in top-25.
В D я научился получать модули всех чисел. как теперь восстановить их(в Large)
Написать ДП за 10000*60 -- суммы всех подмножеств ведь уже известны.
Omg, спасибо
What solution was supposed in C-small? N <= 25, almost all maxtests in the small test =( Too tight for an O(2N * N2) with optimizations that came to my head.
I've splitted cases in two runs.
If that was what intended then it's the first time I see such tight constraints on GCJ. I'm sure there were no solutions with wrong asymptotic authors were trying to cut off, but then why not use n <= 20?..
Nevertheless, respect to everybody who suceeded to the onsite finals.
I'm sure that on fast computer my solution could be optimised twice.
Well, I think it can be solved in O(2^n * n) because we always should go to the fastest person on the left or the fastest person on the right
It can be O(2N·N) (on each step I choose where to go — to the right or to the left). I also return from the function if current answer is worse than current best answer, and it helps a lot.
How to solve B?
First of all let's break all temperatures into k groups. ti will belong to group
i mod k.Then do binary search on the answer D. Let's say the interval which will fit all temperatures will be [L;L + D]. For every temperature ti with i < k you can calculate the range relative to L where ti might be such that all temperatures from its group will fit into [L;L + D] interval. Let's denote this interval for i-th group as [L + mni;L + mxi]. So you have k such intervals, you sum them up and get the final range relative to L, you just need to check if exists L such that this interval will include sums0.
Better than binary search:
Note that we can find si + K - si = sumi + 1 - sumi for any valid i; by repeating it, we can find si + nK - si. Compute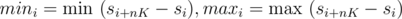 , so that group
, so that group 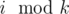 spans the range [si + mini, si + maxi]. Clearly this also means the minimum difference is maxi - mini.
spans the range [si + mini, si + maxi]. Clearly this also means the minimum difference is maxi - mini.
But in fact, this is almost enough; let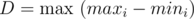 , then the answer is either D or D + 1. To find this, compute
, then the answer is either D or D + 1. To find this, compute 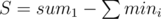 and
and  . If S ≤ T then the answer is D, otherwise the answer is D + 1.
. If S ≤ T then the answer is D, otherwise the answer is D + 1.
The idea is like this. This might not make sense; I'm not sure how to word it.
We know that each group has a difference of minimum and maximum that we cannot change. However, we can try to arrange the groups so that their minima line up. For example, given K = 3, sum = (3, 4, 2, 5, 2), we obtain group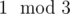 to have s1, s4 = s1 + (4 - 3), s7 = s4 + (2 - 5), group
to have s1, s4 = s1 + (4 - 3), s7 = s4 + (2 - 5), group 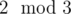 to have s2, s5 = s2 + (2 - 4), and group
to have s2, s5 = s2 + (2 - 4), and group 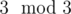 to have s3, s6 = s3 + (5 - 2). In other words, group
to have s3, s6 = s3 + (5 - 2). In other words, group 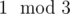 spans [s1 - 2, s1 + 1], group
spans [s1 - 2, s1 + 1], group 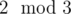 spans [s2 - 2, s2], and group
spans [s2 - 2, s2], and group 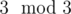 spans [s3, s3 + 3].
spans [s3, s3 + 3].
Now, we begin by lining up everything. Let s1 = x1 + 2, s2 = x2 + 2, s3 = x3, so that our ranges become [x1, x1 + 3], [x2, x2 + 2], [x3, x3 + 3]; this also means x1 + x2 + x3 = - 1.
Now, if we can use fractional temperatures, we can just set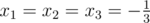 and we're done. But this is not the case, so unfortunately we have to fiddle a little. Let's begin with x1 = x2 = x3 = - 1, and we will increase two of the xi's (may be the same) so that their sum becomes - 1. Our intervals are [ - 1, 2], [ - 1, 1], [ - 1, 2], and we want to slide two of them to the right, trying to keep the difference between minimum and maximum as small as possible.
and we're done. But this is not the case, so unfortunately we have to fiddle a little. Let's begin with x1 = x2 = x3 = - 1, and we will increase two of the xi's (may be the same) so that their sum becomes - 1. Our intervals are [ - 1, 2], [ - 1, 1], [ - 1, 2], and we want to slide two of them to the right, trying to keep the difference between minimum and maximum as small as possible.
Unfortunately, this is impossible without making some of the upper bounds to exceed 2 (there is only one move available, the middle one moved to the right once to [ - 1, 2], [0, 2], [ - 1, 2]), so we must necessarily break the upper bound 2. But now this is always possible; after moving the maximum extent possible, we just move as many intervals as necessary (in this case one more, to [0, 3], [0, 2], [ - 1, 2]). This will never reuse the same interval if we take the starting value of x1, x2, x3 to be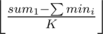 ; that is, the largest equal value for x1, x2, x3 so that their sum doesn't exceed the required sum. The difference to the required sum will be strictly smaller than K, hence why we won't increase the upper bounds. We also won't be able to get rid of the original value - 1, since if we can that means we will increase all K intervals by at least once each, but we don't have that many moves.
; that is, the largest equal value for x1, x2, x3 so that their sum doesn't exceed the required sum. The difference to the required sum will be strictly smaller than K, hence why we won't increase the upper bounds. We also won't be able to get rid of the original value - 1, since if we can that means we will increase all K intervals by at least once each, but we don't have that many moves.
After setting x1 = 0, x2 = 0, x3 = - 1, this corresponds to the solutions s1 = 2, s2 = 2, s3 = - 1, and thus follows s4 = 3, s5 = 0, s6 = 2, s7 = 0, making the sequence s = (2, 2, - 1, 3, 0, 2, 0) which can be verified.
Had sum5 = 3 instead, we have s7 = s4 - 2 (and thus s7 = s1 - 1), making the first interval to be [s1 - 1, s1 + 1] instead, so that we obtain s1 = x1 + 1 and x1 + x2 + x3 = 0. This time we can just set x1 = x2 = x3 = 0, and we're done already, giving s = (1, 2, 0, 2, 0, 3, 0).
Don't mean to invade privacy of any sort here but, who is user "linguo" ranked 5? Does he compete here on CF or on TC?
It's particularly interesting to me as all his solutions are in python which is very rare among the top participants. :)
https://en.wikipedia.org/wiki/Luke_Pebody
WOAH
And he even won Round3 in 2011 by Python: https://code.google.com/codejam/contest/1158485/scoreboard
Couldn't get his solution of D-large.
Added to the gym — 2015 Google Code Jam Round 3 (GCJ 15 Round 3)
rng_58 tomasz.kociumaka tourist Xhark linguo iwiwi tomek simonlindholm kevinsogo vepifanov bmerry fagu dzhulgakov pashka BaconLi betaveros JoeyWheeler yeputons qwerty787788 Merkurev wrong wuzhengkai peter50216 TankEngineer semiexp Romka