UPD. Появился разбор задачи Е. Мы просим прощения за задержку, он получился действительно трудоемким, и, чтобы как-то загладить свою вину, мы публикуем несколько интерпретаций решения.
A. Определение лиц
Автор: Monyura
Для решения этой задачи следует перебрать все квадраты 2х2 и проверить, что переставив буквы можно получить слово "face". Это можно удобно сделать, например, отсортировав буквы квадрата в алфавитном порядке и проверив, что отсортированное множество равно "acef"(Отсортированный порядок букв слова "face").
B. Вечеринка в Looksery
Автор: Igor_Kudryashov
При любом раскладе существует такое множество людей, что, если они придут и разошлют сообщения своим контактам, то каждый сотрудник получит количество сообщений отличное от того, что указал Игорь. Покажем как построить это множество. Рассмотрим 2 случая.
Ни одно из чисел, предложенных Игорем, не равно нулю. Тогда если никто не придет на вечеринку, то всем сотрудникам придет по 0 сообщений, и, следовательно, искомое множество — это пустое множество.
Хотя бы одно из чисел Игоря равно нулю. Пусть он предполагает, что i-ому сотруднику достанется 0 сообщений. В этом случае добавим i-ого сотрудника в искомое множество. Он разошлет сообщения всем своим контактам и у него самого количество пришедших сообщений станет равно 1. При добавлении других сотрудников в искомое множество, количество сообщений, пришедших i-ому не уменьшится, а, значит, его можно удалить из рассмотрения. Для людей из списка контактов i-го сотрудника Игорь предсказал некоторые количества сообщений, и т.к. по одному сообщению этим людям уже пришло, из желаемых Игорем чисел нужно вычесть единицу. После этого можно перейти к той же задаче, считая что у нас имеется n - 1 сотрудников. Если оставшееся количество сотрудников равно 0, то искомое множество построено.
C. Игра чётности
Автор: olpetOdessaONU
Если n = k, то ни один ход не может быть совершен. Победитель определяется изначальной суммарной четностью количества жителей. Иначе заметим, что игрок, который делает ход последним, может гарантировать себе победу, если на момент его последнего хода остаются как четные, так и нечетные города — он просто выберет, город с какой четностью сжечь, чтобы получить нужную итоговую четность. Поэтому задача его противника — уничтожить все города какого-то одного типа. Иногда все равно какого, а иногда — нет, это зависит от имени игрока и четности k. Поэтому дальнейшее решение задачи заключается в сравнении количества ходов (n - k) / 2 «непоследнего» игрока с количествами четных и нечетных городов — хватит ли ходов, чтобы их уничтожить. Если последним ходит Станнис, то, в случае четного k, Дейнерис должна сжечь все четные либо все нечетные города. В случае нечетного k, Дейнерис следует сжечь все нечетные города. Если последней ходит Дейнерис, то, в случае четного k ее противник не имеет шансов на победу, а, в случае нечетного k, Станнис должен сжечь все четные города.
D. Признаки Хаара
Автор: Monyura
Эта задача имела сложное условие, но максимально близкое к реальности.
Один из вариантов решения задачи состоит в изучении структуры ответа. Предположим, что у нас есть ответ, т.е последовательность операций: взятие сумм на префикс-прямоугольнике и коэффициентов, на который умножается сумма. Мы можем менять порядок операций, значение признака при этом меняться не будет. Тогда отсортируем операции по правому нижнему углу прямоугольника. Будем применять операции начиная от последний к первой. Решение состоит в том, что бы не применять операции, которые не нужны и применить все те, которые мы обязаны применить. Для этого для каждого пикселя будем поддерживать коэффициент с которым он сейчас входит в значение признака. Изначально этот коэффициент равен 0. Пройдем по каждому пикселю начиная с нижнего правого угла. Если текущий коэффициент не равен + 1 для пикселя покрытого W и - 1 для пикселя покрытого B, то пиксель входит в значение признака с неправильным коэффициентом и нам надо его поменять, для этого используем одну операцию. Единственный способ поменять значение этого пикселя теперь, после того как все большие и по ряду и по столбцу просмотрены — это взять сумму на префикс-прямоугольнике с правым нижним углом в этом пикселе. Предположим значение коэффициента должно быть X ( + 1 или - 1 в зависимости от цвета), а сейчас равно C. Тогда мы должны прибавить сумму на прямоугольнике с коэффициентом X - C к значению признака. Но сделав это, мы так же прибавим X - C к коэффициентам всех пикселей на префикс-прямоугольнике. Это решение может быть реализовано так, как описано за O(n2m2) или за O(nm).
Так же хочется добавить, что от настоящих признаков Хаара данное определение отличается только тем, что настоящие применяются к региону изображения, а не ко всему изображению. Но минимальное число операций можно посчитать по такому же принципу.
E. Саша Круг
Авторы: Krasnokutskiy, 2222
Сложность авторского решения составляет O((n + m) * h + n * logn + m * logm), где h — максимальное(среди двух множеств) число точек выпуклой оболочки. Ниже будет доказано, что для данных ограничений имеет место более точная оценка O((n + m) * С2 / 3 + n * logn + m * logm), где С — максимальная координата.
Существует две интерпретации решения, мы приведем обе. Для начала докажем независимую оценку на число точек выпуклой оболочки:
Пусть есть множество точек на плоскости с целочисленными неотрицательными координатами. Докажем, что количество точек в выпуклой оболочке, в которой никакие три точки не лежат на одной прямой, равно O(C2 / 3), где C — максимальная координата.
Пусть выпуклая оболочка в порядке обхода против часовой стрелке образуется последовательностью точек P0, P1, …, Pn - 1. Рассмотрим последовательность векторов P1 - P0, P2 - P1, .., Pn - 1 - Pn - 2, P0 - Pn - 1 Обозначим элемент этой последовательности Vi = P(i + 1)modn - Pi. Рассмотрим такие Vi = (xi, yi), что 0 ≤ xi, yi ≤ C. т.е. вектора, лежащие в первой координатной четверти. Заметим, что эти вектора будут идти подряд в последовательности векторов всех четвертей из-за свойств выпуклой оболочки. Докажем, что их количество равно O(C2 / 3), а доказательство для других четвертей будут аналогичны.
Ключевой факт — любая частичная сумма векторов, дает точку из выпуклой оболочки, включая сумму всех векторов. Тогда сумма по каждой координате всех векторов первой четверти не превышает C. Так же, напоминаю, что никакие три точки не лежали на одной прямой в выпуклой оболочке, а значит не существует одинаковых векторов(даже коллинеарных). Посчитаем сколько максимум можно набрать векторов из первой четверти, что бы сумма по каждой координате не превосходила C:0 ≤ sumX, sumY ≤ C. Ослабим ограничения до 0 ≤ sumX + sumY ≤ C, от этого максимальное количество векторов, очевидно, не уменьшится. Будем набирать наше множество жадно, очевидно, что сначала имеет смысл брать вектора с как можно меньшей суммой координат. Возьмем максимальное количество векторов, сумма координат которых 1 , таких векторов всего два: (0, 1), (1, 0). Добавим вектора с суммой 2: (0, 2), (1, 1), (2, 0), их всего три. В общем случаи, если сумма координат равна k, то с такой суммой существует (k + 1) различных векторов. Нам надо набирать вектора до тех пор, пока сумма координат не превзойдет C. Т.е. 1 * 2 + 2 * 3 + 3 * 4 + … + k * (k + 1) = O(C). Можно честно посчитать эту сумму, но её порядок будет O(k3). Отсюда следует, что k = O(C1 / 3). Теперь посчитаем количество векторов, которые мы взяли: 2 + 3 + … + (k + 1) = O(k2). Таким образом максимум можно взять O(C2 / 3) векторов в первой четверти. Во всех других четвертях оценка такая же, из-за соображений симметрии.
Теперь можно переходить к разбору решения.
Первый вариант интерпретации решения, автор Sklyack:
Назовём множества точек A и B разделимыми, если существует окружность, содержащая внутри или на границе все точки одного множества, и не содержащая ни внутри, ни на границе точек другого множества, такую окружность назовём разделяющей. Пусть для определённости точки множества A находятся внутри или на границе окружности, а B -- снаружи. Точки из A на границе разделяющей окружности допускаются, так как немного увеличив радиус, получим A строго внутри, B -- строго снаружи окружности.
Пусть A содержит хотя бы две точки. Разделяющую окружность можно сжать так, что она пройдёт через хотя бы две точки из A. Можно перебрать все пары точек 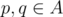 и через каждую такую пару попытаться провести разделяющую окружность. Центр искомой окружности лежит на серединном перпендикуляре отрезка pq. Обозначим точки серединного перпендикуляра как l(t), где
и через каждую такую пару попытаться провести разделяющую окружность. Центр искомой окружности лежит на серединном перпендикуляре отрезка pq. Обозначим точки серединного перпендикуляра как l(t), где 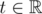 -- параметр. Все точки, не лежащие на прямой pq, ограничивают параметр t сверху или снизу, точки на прямой pq должны лежать за пределами отрезка pq. Например, на следующем рисунке синяя точка ограничивает центр разделяющей окружности слева, а красные точки -- справа, поэтому центр должен лежать внутри отрезка cd.
-- параметр. Все точки, не лежащие на прямой pq, ограничивают параметр t сверху или снизу, точки на прямой pq должны лежать за пределами отрезка pq. Например, на следующем рисунке синяя точка ограничивает центр разделяющей окружности слева, а красные точки -- справа, поэтому центр должен лежать внутри отрезка cd.
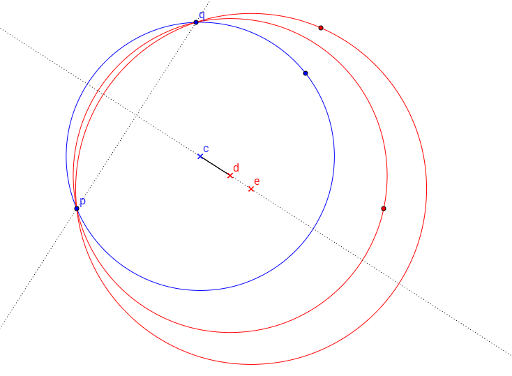
Переберём все точки и проверим, что найдётся значение t, которое удовлетворяет всем ограничениям. Это даёт нам решение задачи за O((|A|2 + |B|2)(|A| + |B|)).
Рассмотрим параболоид z = x2 + y2 и проведём произвольную не вертикальную плоскость ax + by + z = c. Пересечение параболоида и плоскости удовлетворяет уравнению ax + by + x2 + y2 = c, или 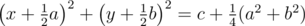 . Если проецировать точки параболоида (x, y, x2 + y2) на плоскость,
. Если проецировать точки параболоида (x, y, x2 + y2) на плоскость, 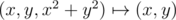 , то сечение параболоида плоскостью проецируется в окружность, точки параболоида ниже плоскости проецируются во внутренние точки круга, выше плоскости -- в точки снаружи круга. Так как соответствие
, то сечение параболоида плоскостью проецируется в окружность, точки параболоида ниже плоскости проецируются во внутренние точки круга, выше плоскости -- в точки снаружи круга. Так как соответствие 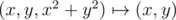 взаимно-однозначно, то верно и обратное: при проекции точек плоскости на парабалоид
взаимно-однозначно, то верно и обратное: при проекции точек плоскости на парабалоид 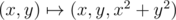 окружность проецируются в сечение параболоида плоскостью, внутренние точки -- в часть параболоида ниже секущей плоскости, внешние -- выше плоскости.
окружность проецируются в сечение параболоида плоскостью, внутренние точки -- в часть параболоида ниже секущей плоскости, внешние -- выше плоскости.
Таким образом, проекция точек на параболоид задаёт взаимно-однозначное соответствие между окружностями и плоскостями (не вертикальными), а для разделения множеств A и B точек плоскости окружностью достаточно разделить их трёхмерные проекции на параболоид A′ и B′ не вертикальной плоскостью. Такую плоскость назовём разделяющей (при этом по аналогии с разделяющей окружностью, разделяющая плоскость может содержать точки из A′).
По аналогии с разделяющей окружностью, разделяющую плоскость можно провести через две точки множества A′. При этом остальные точки A′ будут лежать ниже или на плоскости. Другими словами, разделяющая плоскость пройдёт через ребро верхней выпуклой оболочки множества A′. При проекции рёбер верхней выпуклой оболочки A′ на плоскость xOy получится некоторое разбиение плоской выпуклой оболочки множества A непересекающимися рёбрами, а разделяющей плоскости соответствует разделяющая окружность, проходящая через ребро разбиения. Обозначим выпуклую оболочку A как coA. В случае, когда никакие 4 вершины coA не лежат на одной окружности, все грани верхней выпуклой оболочки -- треугольники, а полученное разбиение -- триангуляция. В противном случае, достроим полученное разбиение до триангуляции.
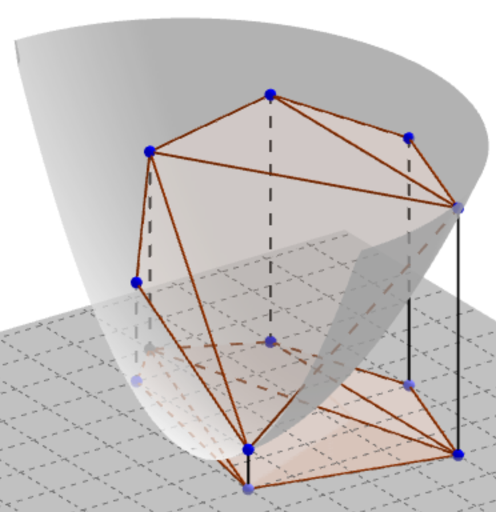
Для построения разделяющей окружности достаточно перебрать рёбра триангуляции и проверить возможность провести окружность через ребро как описано выше.
Полученная триангуляция характеризуется следующим свойством: окружность, описанная около любого треугольника, содержит весь многоугольник coA, так как соответствующая грань трёхмерной выпуклой оболочки проходит выше, чем все трёхмерные точки A′. Эта триангуляция "противоположна" триангуляции Делоне, в которой окружность, описанная около любого треугольника, не содержит внутри других точек исходного множества. Её можно назвать триангуляцией Анти-Делоне, вроде бы такой термин где-то используется.
Используя характеризующее свойство, триангуляцию Анти-Делоне можно построить методом "разделяй и властвуй" без перехода в трёхмерное пространство, работая только с точками плоскости и окружностями. Пусть мы триангулируем многоугольник, образованный вершинами coA при обходе против часовой стрелки с i-й по j-ю. Найдём третью точку треугольника, в который войдет ребро (i, j), то есть такую точку k, что окружность, описанная около треугольника (i, j, k), содержит текущий многоугольник. Для этого переберём вершины текущего многоугольника и выберем ту, которая даёт крайнее положение центра описанной окружности на серединном перпендикуляре ребра (i, j). Окружность будет содержать весь многоугольник coA, так как ребро (i, j) входит в триангуляцию Анти-Делоне. Рекурсивно триангулируем многоугольники с вершинами с i-й по k-ю и с k-й по j-ю. База рекурсии -- отрезок, его триангулировать не нужно.
Для решения исходной задачи следуют поменять множества A и B ролями и ещё раз применить описанный алгоритм. Вычислительная сложность решения составляет O(|A|log|A| + |coA|(|coA| + |B|) + |B|log|B| + |coB|(|coB| + |A|)=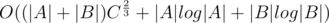 , где C — максимальное абсолютное значение координат заданных точек.
, где C — максимальное абсолютное значение координат заданных точек.
Вторая интерпретация, автор 2222:
Предположим, что возможно построить разделяющую окружность. Тогда обозначим множество точек внутри окружности как A, а множество точек снаружи, как B.
Для простоты описания решения, предположим что никакие 4 точки не лежат на одной окружности. В таком случае, если мы найдём разделяющую окружность, проходящую через несколько точек, то мы всегда сможем немного увеличить радиус и, возможно, немного сдвинуть окружность так, чтобы одно множество точек стало лежать строго внутри окружности, а другое — строго снаружи.
Обозначим множество вершин выпуклой оболочки множества A как CH(A), тогда один из вариантов решения задачи — перебрать пары точек из CH(A) и попытаться провести через них окружность, которая содержит все точки CH(A) (а следовательно, и все точки A), а все точки из B лежат снаружи, или на границе окружности. Обозначим пару точек из CH(A) как p и q. Так как все точки из CH(A) должны лежать внутри окружности, а все точки из B — снаружи, то каждая из этих точек задаёт некие ограничения на радиус окружности и на расположение центра окружности относительно прямой, проходящей через точки p и q. Например, на следующем рисунке, точки c, d и e — центры синей и красных окружностей. Заметим, что любая окружность с центром на отрезке cd будет содержать все синие точки, а все красные точки будут снаружи или на границе окружности.

Таким образом, мы можем проверить существует ли разделяющая окружность, проходящая через точки p и q, просто проверив вступают ли ограничения на разделяющую окружность в противоречие или нет, это можно сделать за 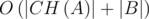 . Cложность всего алгоритма составит
. Cложность всего алгоритма составит 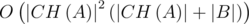 . Для того, чтобы понять быстро это или нет, воспользуемся следующим фактом:
. Для того, чтобы понять быстро это или нет, воспользуемся следующим фактом: 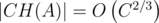 , где C — максимальная по модулю координата точек из A, тогда сложность алгоритма составит O(C2 + C4 / 3|B|). Очевидно, что этот алгоритм слишком медленный, чтобы уложиться в лимит по времени.
, где C — максимальная по модулю координата точек из A, тогда сложность алгоритма составит O(C2 + C4 / 3|B|). Очевидно, что этот алгоритм слишком медленный, чтобы уложиться в лимит по времени.
Назовём пару точек Ai, Aj хорошей, если существует окружность, проходящая через эти точки, которая содержит в себе все точки CH(A).
\textbf{Лемма 1}. Если каждую хорошую пару точек соединить отрезком, то никакие 2 отрезка, соответствующие 4-ем различным точкам, не пересекаются.
Допустим, что это не так, тогда существуют 2 разные окружности с хордами ab и cd соответственно, такие что точки a, b, c и d лежат внутри или на границе этих окружностей.
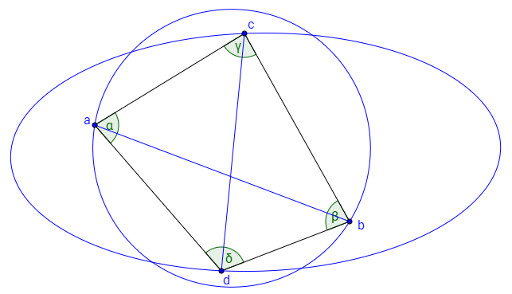
Так как точки c и d лежат внутри окружности с хордой ab, то α + β < π, аналогично точки a и b лежат внутри другой окружности, поэтому γ + δ < π, где α, β, γ и δ углы при a, b, c и d соответственно в четырёхугольнике с вершинами в этих точках. Но так сумма углов четырёхугольника равна 2π, то получили противоречие, значит лемма 1 верна.
Пронумеруем вершины CH(A) по часовой стрелке от 1 до h, обозначим i-ую вершину CH(A) как chi. Построим рекурсивную процедуру нахождения всех хороших пар точек на промежутке [i..j], при условии, что пара точек (chi, chj) хорошая. Выберем на промежутке [i + 1..j - 1] такое k, что окружность проходящая через chi, chj и chk содержит CH(A), а следовательно пары точек (chi, chk) и (chj, chk) являются хорошими. Заметим, что такая окружность всегда существует, так как пара (chi, chj) является хорошей. Такое k можно найти за O(j - i) по аналогии с алгоритмом нахождения разделяющей окружности проходящей через 2 точки. Теперь решим задачу для [i..k] и [k..j]. Заметим, что пара точек (ch1, chh) является хорошей, так как соответствующий отрезок является ребром выпуклой оболочки, поэтому для решения всей задачи, выполним данную процедуру для промежутка [1..h]. Данная рекурсивная процедура имеет сложность O(h2) и будет вызвана h - 1 раз, а значит количество хороших пар — O(h).
Финальный алгоритм выглядит следующим образом. Переберём все хорошие пары точек, для каждой пары, найдём разделяющую окружность, которая проходит через эту пару точек. Если разделяющая окружность не была найдена, то поменяем множества A и B местами и повторим процедуру. Сложность данного алгоритма составляет 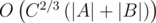 .
.
Для того, чтобы не было проблем с точностью, необходимо все вычисления делать в целых числах.
F. Юра и разработчики
Автор: Rubanenko
Посмотрим на следующее решение:
Пусть f(l, r) — это решения для подмассива [l, r]. Легко заметить, что f(1, n) — это ответ на поставленную задачу. Как считать f(l, r)? Пусть m — это индекс максимального элемента подмассива [l, r]. Все хорошие подмассивы могут быть разбиты на два непересекающихся множества: те, которые содержат m, и те которые его не содержат. Чтобы посчитать последние можно просто вызвать f(l, m - 1) и f(m + 1, r). Осталось посчитать количество "хороших" подмассивов, которые содержат m, другими словами, количество пар (i, j), что l ≤ i < m < j ≤ r и g(i, m - 1) + g(m + 1, j)%k = 0 (g(s, t) означает as + as + 1 + ... + at). Пусть s — это последовательность частичных сумм массива из условия, то есть si = a1 + a2 + ... + ai. Для всех j нам интересно количество i, что sj - si - am%k = 0, так что если мы переберем все возможны j, то нам интересно количество таких i, что si = sj - am(modk) и l ≤ i < m. Имеем ряд запросов на отрезке вида "сколько есть чисел на отрезке (l, r), что они равны x". Это можно сделать за O(q + k) времени и памяти, где q — количество запросов, которые сгенерировались в ходе рекурсивного вычисления f(1, n). Авторское решение обрабатывает эти запросы в режиме оффлайн, с помощью массива подсчета.
Можно заметить, что в худшем случае мы получим O(n2) запросов, которые очевидно не дадут уложиться в ограничения. Тем не менее, мы можем выбрать, что быстрее: перебрать все возможные j или i. В обоих случаях мы получаем простую сравнимость и запрос на отрезке, описанный выше. Если идти только по меньшему отрезку, то каждый раз, как мы "проходим" по элементу w, он переходит в отрезок, который, как минимум, в два раза меньше, чем тот, которому он принадлежал до этого. Таким образом, каждый элемент окажется в отрезке единичной длины(база рекурсии) за O(log(n)) "проходов" по нему.
Сложность алгоритма O(n × log(n) + k).
G. Счастливая очередь
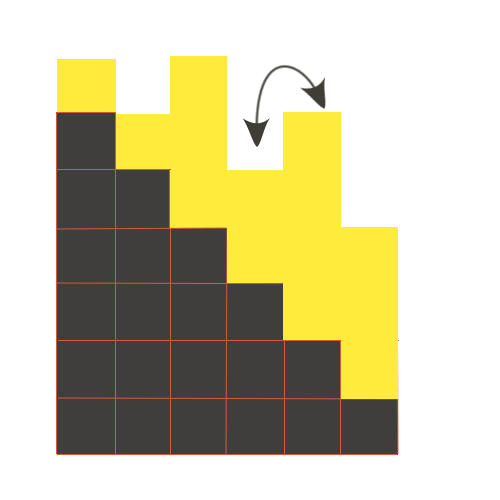
Давайте переформулируем условие в терминах башен определенной высоты, которые будут находиться на лестнице. Тогда количество денег соответствующего человека в очереди будет равно высоте башни вместе с высотой ступеньки, на которой башня стоит. А процесс продвижения в очереди будет эквивалентен подъему одной башни на ступеньку вверх, а та, на чье место она взошла — вниз, как показано на иллюстрации. Тогда, становится очевидно, что чтобы все башни на ступеньках были отсортированы, достаточно отсортировать башни без учета высот ступенек. Итого сложность сортировки O(nlog(n)).

H. Вырожденная матрица
Автор: Igor_Kudryashov
У вырожденной матрицы строки линейно зависимы, а значит можно представить матрицу B в следующем виде:
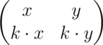
Пусть

Положим, что элементы первой строки матрицы A являются координатами точки a0 на двухмерной плоскости, а элементы второй строки — координатами точки a1. Представим, что строки матрицы B также являются координатами точек b0 и b1. Заметим, что в этом случае прямая, проходящая через точки b0 и b1, также проходит через точку (0, 0).
Будем искать ответ на задачу — число d — бинарным поиском. Предположим мы зафиксировали некоторое число d0 и хотим проверить, существует ли такая матрица B, что

В геометрической интерпретации это означает, что точка b0 находится в квадрате, с центром в точке a0 и длиной стороны 2·d0, а точка b1, соответственно, в квадрате с такой же длиной стороны и центром в a1. Таким образом, нам нужно проверить, существует ли прямая, проходящая через точку (0, 0) и пересекающая эти квадраты. Чтобы это сделать, достаточно перебрать вершины одного квадрата, построить прямую, проходящую через выбранную вершину и центр координат и проверить, что она пересекает какую-нибудь из сторон второго квадрата. Затем нужно сделать то же самое, обменяв квадраты. В итоге, если прямая нашлась, то нужно уменьшить границу поиска, иначе расширить.










В задаче H при минимальном ответе прямая проходит сразу через вершины обоих квадратов, то есть элемены ||A-B|| по модулю одинаковы. Получаем 8 квадратных уравнений, решаем каждое, берём минимальный ответ.
А еще можно ограничиться только линейными уравнениями (почему, кстати?). 11478456
Линейные уравнения, кстати, соответствуют случаям, когда det(A — B) = 0
В F можно сделать (относительно) простой divide-and-conquer : для того, чтобы посчитать число хороших отрезков, полностью входящих в [l, r), надо сложить число отрезков, входящих в [l, m) или [m, r), где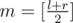 , а также число хороших отрезков, пересекающихся как с [l, m), так и с [m, r). Первые два слагаемых считаем рекурсивно. Для подсчёта третьего слагаемого переберём, в какую половину попадёт первый максимальный элемент хорошего отрезка (именно первый максимум выбирается, чтобы не посчитать отрезок 2 раза).
, а также число хороших отрезков, пересекающихся как с [l, m), так и с [m, r). Первые два слагаемых считаем рекурсивно. Для подсчёта третьего слагаемого переберём, в какую половину попадёт первый максимальный элемент хорошего отрезка (именно первый максимум выбирается, чтобы не посчитать отрезок 2 раза).
Пусть, например, первый максимум попал в левую половину (то есть в [l, m)). Посчитаем префиксные максимумы в правой половине и суффиксные максимумы в левой. Будем перебирать левую границу нашего отрезка в порядке убывания (она всегда лежит в [l, m)), а при это поддерживать максимальную такую правую границу, что первый максимум на отрезке лежит именно в левой половине (такая правая граница движется только вправо, так как префиксные максимумы не убывают), сумму на текущем отрезке в левой половине, сумму на текущем отрезке в правой половине и массив
cnt—cnt[x]равно количеству уже рассмотренных префиксов второй половины, сумма на которых равна x по модулю k. С помощью таких данных несложно пересчитывать ответ.Случай с правой половиной почти аналогичен с точностью до строгости/нестрогости неравенств.
Код: 11475666 (хак с
cntиvaluesпозволяет быстро обнулять массив).Крутое решение и хак с обнулением
H можно попроще, так же перебираем d получим 4 неравенства: |a - a'| < d |b - b'| < d, |c - c'| < d, |d - d'| < d, где a, b, c, d — элементы матрицы А, а a', b', c', d' — элементы матрицы B. Из неравенств мы получим 4 отрезка — какие значения могут принимать a', b', c', d', а значит можем узнать, какие значения могут принимать произведения k = a'd' и l = b'c'. Если отрезки возможных значений k и l пересекаются (то есть B может быть выражденой), то существует матрица B удовлетворяющая всем условиям, сдедовательно, answer ≤ d, иначе answer > d.
Код: 11465692
I still don't know what problem D was asking for. What is this value, why are we multiplying etc Can someone please clarify?
You have an n*m matrix initially containing zeroes. You have a pattern of W's and B's, and want to transform the matrix such that it has a 1 where the pattern has a W, and a -1 where the pattern has a B. The only allowed operation is "add k to each position in this rectangle whose topleft is the topleft of the matrix, for some integer k". What is the minimum nummer of operations?
How on earth did you unravel this enigma? Thanks a lot though!
Jeez! Thanks for clarification. I would have had more chance understanding the problem without reading the problem statement :/
E. Sasha Circle
Authors: Krasnokutskiy, 2222
Coming soon???
Am I the only one who found it impossible to understand problem D's statement?
No No No No
I was going to abondon it at some time (especially the first time I read it)
of course NO!
In my opinion, it is good example, when easy problem complicated an incomprehensible statement to make this problem more difficult.
I thought D's statement was straightforward. I suspect the confusing aspect for all of those who found it incomprehensible was the gap between face detection and Haar features, i.e. why would we want to compute such features. Maybe once we lose the thread of motivation, things become harder to understand?
I wanted to describe the Haar features usage at a face detection but then look at the amount of text :)
Yes, peer review sometimes mutilates a problem's enlightenment potential. But well done for trying to teach Viola-Jones to 5000 people! (Worked for me, by the way. Now I know more than just the famous name.)
Don't read this xd
k = 106
Omg, I'm such a moron >_>
I was reading problem D. When I perfectly understood problem D, I found that contest is over.
I can't open the problemset... Any ideas why, it shouldn't be blocked anymore, right?
On problem B, I believed that by
it was meant that
because of my distrust in English statements of contests made by Russian-speaking guys. :/
In Problem C,
Shouldn't this be
yes, you're correct. there is an error in the editorial.
Fixed, thank you!
Problem H could be solved in O(1) without any binary search. Consider the case when a, b, c, d ≥ 0. Then define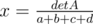 . One may note,
. One may note,
Take B as the above matrix. Then the answer in this case equals |x|. (But we strictly proved only that answer $\leq x$ ).
If some of a, b, c, d are negative, this also holds, but better answer exist. We wanna get |a| + |b| + |c| + |d| in the denominator of x. One may note that if we have an even number of negative elements, it is possible to use the same B matrix, but reverse somewhere signs for x'es (and get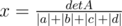 , and |x| as an answer). For example, if a < 0 and c < 0, we take
, and |x| as an answer). For example, if a < 0 and c < 0, we take
Only essential case is if we have an odd number of negative elements in initial matrix. Then we have to subtract minimal element of (|a|, |b|, |c|, |d|) instead of adding, and answer equals
However, I was unable to prove the minimality of x chosen this way during the contest (but solution got AC). Any ideas?
Hey! Really nice idea. :)
How did you come up with such an idea in the very beginning?
I found this code in the announcement page. Is this same as yours? Though it seems different. http://codeforces.me/contest/549/submission/11467650
You can come up with such an idea when you see at example tests. Futhermore, this idea is similiar to Equioscillation theorem (http://en.wikipedia.org/wiki/Equioscillation_theorem) from numerical analysis, which is used to finding polynomial of bounded degree, that maximal absolute value of difference between given function and this polynomial is as smallest as possible. This helped me with coming up with similiar idea.
this idea is really fantastic! sadly i failed to deal with the negative elements...
math is awesome
My approach was similar. I proved it using contradiction which I hope is correct. Let the optimal solution be x and x ≠ xd. Thus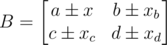 (It doesn't matter where we put x due to symmetry).
(It doesn't matter where we put x due to symmetry).
Since det(B) = 0, (a ± x)(d ± xd) = z1 . I won't make it lengthy, but it can be easily proved that there is an optimal mid value xd < x' < x which can replace both x and xd, contradicting the optimal solution x itself. Similarly we can assume xb = xc. Moving on, again assume x to be the optimal answer.
How can Problem D can be implemented in O(n,m)?Can someone please explain?
Check 11483301.
Create an array b, such that b[i][j] = 1 if (i, j) is white and b[i][j] = - 1 if (i, j) is black.
Keep a counter for the answer. For every (i, j), we want to determine if we need a rectangle whose bottom-right vertice is (i, j). The rectangles (except the one whose bottom-right vertex is (i, j)) containing (i, j) must also contains (i + 1, j) or (i, j + 1), so the sum of those rectangles' values is b[i + 1][j] + b[i][j + 1]. But, we will count some rectangles twice, those containing both (i + 1, j) and (i, j + 1), which must contain (i + 1, j + 1)! So, the effect of previous rectangles on (i, j) is b[i + 1][j] + b[i][j + 1] - b[i + 1][j + 1]. If this value doesn't equal b[i][j], we'll need another rectangle whose bottom-right corner is (i, j), so we increment the counter.
Cool trick,definitely going to remember this.Thanks johnathan
I don't get it. Could somebody explain it in other words (maybe even with pictures)? :)
My understanding of this problem might be wrong, but let me try. We will start operations from rectangle (0, 0, n, m). This way we satisfy at least point (n, m), forget about it and move on. Now all array is filled with -1's or 1's. Find next point that is not ok and do operation again. Now, for every point (i, j), how will all bigger rectangles (0, 0, i+a, j+b) effect it? Effect is b[i+1] + b[i][j+1] — b[i+1][j+1]. By effect I mean this. If we want to satisfy point (x, y) we add some value to all rectangle (0, 0, x, y). This effects points (0, 0), (0, 1), (1, 0), (1, 1) and so on to point (x, y). Hope I got it right and my explanation is not misleading :)
Be careful, this is not always possible (if the top row is 0).
Then we will not write 0,0 in the top row. Suppose the 2 points are (0,0) and (6,5). We will write in the following way.
Edit: Oh..u r right...The one with the (0,0) in top row is also degenerate but cannot be written in that form.
ad-bc=0. => ad=bc => b/a=d/c = t (problem is here. if a=0 or c=0. Then we cannot write like this) => b=at and d=ct.
in problem B, in the second case,
solution said: Suppose Igor thinks that i-th employee will receive 0 messages. Then we should add i-th employee in the desired set.
why we should add i-th employee? maybe we don't add i-th employee and we add someone else that messages him.
You forgot that every employee is messaging himself.
No, DartJaf means why i-th employee MUST be selected. Think of the case: 110 010 011
You can select 1th and 3rd employee to send 2 messages to 2nd employee.
i got it!
with the strategy that explained in the solution we can solve any input and there is no "no solution"! if for some input this method dose not give us a solution then we can ask: why you choose i-th people while you have other choice.
so this should is different from that should!!
i had the same doubt as you did, but your words inspired me a lot!
since there's N+1 possible value for A_i, but only N employees in total. so with the method mentioned above there's always a solution to the problem! so we don't have to consider other ways to construct but just to select the point itself is OK!
Problem H, suppose we use binary search to check answer d. Let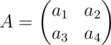 .
.
We want to check if there exists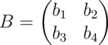 , such that |bi - ai| ≤ d and b1b4 = b2b3.
, such that |bi - ai| ≤ d and b1b4 = b2b3.
Since a1 - d ≤ b1 ≤ a1 + d and a4 - d ≤ b4 ≤ a4 + d,
we have min(S) ≤ b1b4 ≤ max(S).
where set S = {(a1 - d)(a4 - d), (a1 - d)(a4 + d), (a1 + d)(a4 - d), (a1 + d)(a4 + d)}.
Similarly, we can calculate the upper and lower bounds of b2b3.
If the range of b1b4 and b2b3 intersect, d is a possible answer; otherwise not.
Your explanation is so helpful! Thank you! And I saw someone use another way to solve problem H, just like this. I have difficulty proving its correctness. Please help me!
below is some part of your solution can you please tell me logic behind this..
REP(i, 10000) { double m = (lb + ub) / 2; auto p1 = mm(a, d, m); auto p2 = mm(b, c, m); if (p1.second < p2.first || p2.second < p1.first) { lb = m; } else { ub = m; } }
It's just binary search.
-
lb: current lower bound-
ub: current upper bound-
m: mid-point of the two bounds, corresponds to d in my previous explanation-
mm: a function returning the ranges of a * d and b * cIf those ranges don't intersect, then m is not large enough, let lower bound = m; otherwise m is large enough, let upperbound = m
your solution is awesome but why did you looped till 10000 in ur solution ?
I see most people use 100 times only. But I thought 10000 should also fit the time limit easily.
You could also stop when the difference between upper and lower bounds is less than 10 - 6.
can someone explain solution of problem H by binary search.
I hope my comment above is helpful.
Does anyone know how to avoid getting WA on Pretest 10 on Problem E?
I cannot understand why and how the solution of problem G is working. Can anyone explain more? :|
We have an array of persons (we will call it persons, persons[n - 1] — the head, persons[0] — the tail). For each person we will calculate this number val = money of a person — (number of steps to reach the head of the queue). Next we sort persons by val.
Suppose there is an answer ans. (ans[0] — the tail, ans[n - 1] — the head). ans[i].money — how much money is left with ith person in ans.
persons[n - 1].val ≥ ans[n - 1].money, so we can transform the answer so that persons[n - 1] is in the head.
persons[n - 2].val + 1 ≥ ans[n - 2].money, so again we can transform the answer. Why val + 1? Because we need to get to n - 2, no to n - 1.
Then persons[i].val + (n - i - 1) ≥ ans[i].money. So you can put persons[i] in the ans on ith position with money persons[i].val + (n - i - 1).
Excuse me for my mistakes.
http://codeforces.me/contest/549/submission/11481852
P.S. If we want to move a person to a specific position, then no matter which steps we take, the person will be left with the same amount of money. I think that's the main observation.
Hi dears The contest was not bad,but question D has been translate to English very badly...!
I have to read problem D for more than 15 times :D
Lol :D. I thought it happend just for me :D
For problem C I am thinking in a greedy manner . Initially I can find whether my total sum is even or odd store the parity in a variable sum and accordingly maintain two variables which would store count of even and odd numbers present . Now say the player A wins when the total sum of remaining cities is odd and B wins when the total sum is even. When looping through N-K(Number of cities to destroy) if parity of my sum is even then A would try to take an odd number in doing so count of odd number would be decreased and parity of my sum would be flipped and accordingly B would also approach in a similar manner . If at any time in between the loop if count of a variable goes to 0 then other player wins else after the loop has completed we check the sum variable if it is 1 A wins and if 0 B wins . Is this intuition right ?
This statement is already incorrect. If the count of a variable goes to 0, then the game is fully determined afterwards, but it's not true that the other player wins. (For example, if Daenerys destroys the last odd city, then Daenerys is the winner, not Stannis.)
I did not understand one bit, the explanation for problem G. Can someone please explain a little more clearly? Thanks
Nor did I ...
I had to read some solutions from some top coders to figure it out on my own.
Denote A[i] as the money of the ith person standing in the queue. First realize that the coin difference after performing a number of swaps ultimately depends on the absolute displacement of each person. In other words, if a person was at position i, their position changed to j, and they had c money initially, then their new amount would be c + (i - j).
So instead of performing the +1 and -1 operations we will increase the money of each person standing at i by i, i.e., A[i]: = A[i] + i. After we performed some swaps, we then subtract the money of the person standing at j by j, i.e., A[j]: = A[j] - j. This is equivalent to gaining i - j units at the end.
Now, after we increased every A[i], we must sort the array, and we must check if A[i] is strictly increasing because if A[i] = A[i + 1], then A[i] - i > A[i + 1] - (i + 1), and this would mean, we failed our original goal.
That made it very clear, thanks a lot :)
Just to add a final bit to your nice explanation:
Why we sort after adding i to every A[i]?
Ans: Consider a permutation of the A[i] + i different from the sorted order and now subtract j from A[j]. Now some consecutive pair of elements exists such that A[j] > A[j + 1]. The equality A[j] - j ≤ A[j + 1] - (j + 1) should hold. Which cannot hold if A[j] > A[j + 1]. Hence, we need to sort.
That's cool. But how could someone possibly come up with the idea of those towers and stairs of the tutorial or adding i to A[i]? Pretty much 'bolt from the blue'. :P
On a serious note, how to actually come up with such an idea?
Indeed, I think that solving this problem is much easier than understanding this explanation xD. Just note that money+position is an invariant for each person and there's nothing left to be done here.
I don't quite get your point — It's an invariant... so what?
Sooo, if rightmost man needs to have largest amount of money then he needs to have largest value of (money+position) and so on, so we need to sort them by that invariant and check if that's a valid arrangement.
Nice Swistakk! Something to add to the arsenal of solving techniques:
Find an invariant. Establish a realtion to the problem.
Lots of physics problems are solved that way.
Thanks for appreciation, but keep in mind that my thought process was not like "Let's find an invariant! Hmm, money-position doesn't work, money*position also, oh, money+position works!" rather "Hmmm... If guy walks one unit to right he loses one coin and if he walks one unit to left he gains one coin, so money+position is invariant!"
Thanks for showing your thought process.
Here's ITDOI's solution for H that is O(1) : 11490362
It is based on the guess that there is one desired matrix B, which entries of matrix A-B have equal absolute values! (like two sample tests)
Can anyone prove it please?
looking for proofs too
I made almost the same thing.The idea is that when you are binary searching, you obtains 2 intervals which have to intersect.if x is bigger, the intersection is bigger, and you want the smallest x, so the intersection must be exactly one point.For that, left part of the first interval must be equal to the right one of the other, and the limit cases are obtain using a difference equal to either -x, either x.In my solution I fixed the signs of difference for each cell, but is still O(1)
Generally I can prove it in a way acceptable to some people, but not really formal:
Suppose
where |a| < |b|. We'll prove that such B cannot be optimal.
Let's apply some small variation to matrix B:
where δ has the same sign as b. Then if |δ| is small enough then norm of A - B' will be |b - δ| which is obviously less than |b|. QED.
I'm not buying it. What if number of entries with biggest absolute value is bigger than 1 and less than 4? There are lots of such cases.
Ok, this is what will work in more generic case:
Worst case you have 3 biggest values (let's say all except bottom right). Then let's say,
and the signs are chosen in such way that the absolute value of corresponding elements in A - B are improved. Then can be determined in such way that
can be determined in such way that 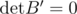 .
.
so you say that this code should not be accept?!
No, on the contrary I actually claim it's possible to prove this approach.
thanks
If we see A as two vectors, then adding B is like adding a couple of parallel vectors of possibly different lengths to these two column vectors of A (because B is degenerate). So we can slide these two column vectors on parallel rails in a direction and by distances that we choose. Now, if there is a line in 2D, I think it's easy to see that the point on the line that is nearest the origin, in the Manhattan metric, is going to always lie on the corner of some axis-aligned square centred on the origin. (In other words, either on the line x = y or x = -y.) So we have two such squares for some choice of B, and they must be of equal size, because otherwise we would rotate the line of B to reduce the size of the larger one (we can always do that because for some choice of B it goes to zero). There is always a solution for which the column vectors of A-B are opposite corners of such a square. (Which, by the way, means that A-B is also degenerate.)
Thanks, now it's been clear for me ;)
wonder why is problem E's still coming soon?
just cant wait XD
why was i getting downvote?
anyone please tell me why?
really that comment was before the update of the tutorial....
I dont know if someone already realized that and discussed here, but the editorial for C is wrong when says: "If Stannis makes the last move and k is odd, Daenerys should burn all the odd or all the even cities...", the correct is even.
sorry for my bad english, and please correct me if I'm wrong or i misunderstood the editorial.
This might be useful for Smallest enclosing circle
For problem E can it not be done by finding out convex hull for one set of points then find two most distant points on the boundary of convex hull, with the mid-point between these two points as center and half of distance as radius we can create a circle covering all the set-one points. Next we can check one by one for the points from other set if they lie outside the circle.
First of all, the circle that you described won't necessarily contain all the points from the convex hull, for example : (0, 0), (1, - 2), (4, 0), (1, 2). And even if it does, the circle could contain also some points from another set so it couldn't be taken as an answer, but answer could exist.
For problem E, why finding out the smallest enclose circle and check if there's one point from the other set in the circle to decide the answer can't be accepted?
Here's a counterexample: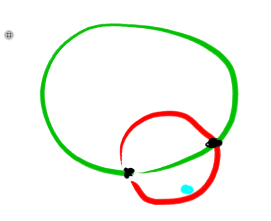 The red circle doesn't work, but the green circle splits the black and blue points. EDIT: To strengthen the counterexample, add another blue point somewhere above the diagram.
The red circle doesn't work, but the green circle splits the black and blue points. EDIT: To strengthen the counterexample, add another blue point somewhere above the diagram.
tourist solved 549D - Haar Features using BigInteger in java. submission : 11464258 He might think the difference that should applied to the image increases exponentially. Can anyone explain how the maximum difference increases according to N?
In problem B, why choosing the position with zero requirement is optimal? Why not someone who can message him?
We want to guarantee that already picked people got more than a[i] messages. If the next person to pick got less than a[i] messages then there is no guarantee that the person will have got the number of messages not equal to a[i] by the end. But.. If you pick a person which got a[i] messages, then he will get +1 from himself. So, we satisfied the requirement that "already picked people got more than a[i] messages". If there is no person which got a[i] messages, then we should not invite them to the party.
I am asking why a solution is not possible by taking someone who sends the guy a message if we do not get a solution by taking the sane guy?
In problem F , how do we find number of occurrences of a number of O(Q + K) time ? , i used a vector and lower_bound but in worst case its (Q * log(N)) . How to do it in O(Q + K) time ?
If you have queries like how many times S[pos] = val with L <= pos <= R (So you have parameters L, R and val), you cand count how many times you have S[pos] = val with pos <= R and than subtract the number of position pos such that S[pos] = val ans pos < L. This way you have just queries like how many values equal to val are on some prefix. You can keep some STL vector, storing in v[i] all val of all the queries on prefix i. Now you can just iterate with i from 1 to N and at this step process the queries on prefix i (keep in parallel a frequency array). Here is my source: http://codeforces.me/contest/549/submission/12921309 .Look at fucntion add_query and at the end where ai process the queries for better understanding
why these two images from the last problem dose not appear well?!
I tried many browsers and none of them showed these images!!
would anyone please explain this method for solving 549H - Degenerate Matrix
Pictures for H are 404'ing... maybe Monyura or someone else can reupload them?
E is much harder than a 2700 problem, even tourist didn't solve it during contest. Why is it rated only 2700?