Можно найти всю информацию о столкновениях i-той машинки в i-той строке матрицы A. А именно, если в i-той строке есть хотя бы одна из цифр 1 или 3, то i-тая машина не является хорошей (она перевернулась при каком-то столкновении). Иначе, i-тая машина — хорошая. Теперь нам просто нужно проверить это условие для каждой машинки.
Можно заметить, что если si = ti для некоторого i, то значение pi для нас не важно. В самом деле, если pi равно si, то оно также равно и ti. И если pi не равно si, то оно также не равно и ti. Так мы получаем ответ, который одновременно ближе или дальше от обоих строк s и t.
Тогда нам интересны такие позиции i, что si ≠ ti. Если мы положим pi равным si мы увеличим расстояние от p до t. Если мы положим pi равным ti то мы увеличим расстояние от p до s. Это означает, что нам необходимо разделить эти позиции на две равные по количеству группу, чтобы получить равноудалённую строку. Например, мы можем сделать так, чтобы первая из этих позиций была ближе к s, вторая к t и т.д. Если таких позиций чётное количество, то мы получим ответ, если нечётное, то ответа не существует.
Временная сложность — O(n).
Задачу можно решить с помощью динамического программирование или с помощью жадного алгоритма. Начнём с динамики.
Обозначим через stayi, lefti and righti наибольшее количество деревьев, которые дровосеки могут повалить, если существует только деревья с номерами с 1 по i, и i-тое дерево не срублено, i-тое дерево срублен и повалено влево, i-тое дерево срублено и повалено вправо соответственно. Теперь мы можем посчитать эти значения для каждого i от 1 до n за O(n) времени, потому что для вычисления каждой следующей величины нам нужно только две предыдущих. Ответом будет наибольшее из stayn, leftn, rightn.
Также эту задачу можно было решить жадным алгоритмом. Давайте повалим самое левое дерево влево (это никогда не ухудшает ответ). После этого, попробуем повалить следующее дерево. Если мы можем повалить его влево, сделаем это (потому что это также никогда не ухудшает ответ). Если не можем, тогда пробуем повалить вправо. Если это возможно, делаем это. Последний шаг справедлив, потому что сваливание некоторого дерева вправо может помешать только сваливанию следующего дерева. Так что мы можем "обменять" одно дерево на другое, не ухудшив ответа.
Временная сложность — O(n).
Можно решить задачу с помощью жадного алгоритма. Докажем, что всегда можно найти ответ (очередь с наибольшим числом довольных людей), в которой все довольные люди стоят вначале очереди. Предположим противное — существует позиции i и j, такие что i < j, все люди с i-го по j - 1-го недовольны, а j-тый человек доволен. Тогда просто поменяем местами людей на позиции i и j. После этого люди на с i-го по j - 1 будет по-прежнему недовольными (или некоторые станут довольными), а j-тый будет по-прежнему довольным. Таким образом, ответ не ухудшился.
Значит, нам нужно находить человека с минимальным ti, который можно обслужить сейчас и он будет доволен. Это можно сделать, отсортировав всех людей по возрастанию ti и пробуя обслуживать их по очереди. Если кто-то будет недоволен, можно отправить его в конец очереди и не добавлять время на его обслуживание к текущему времени ожидания.
Временная сложность — — O(n + sort).
Это правда, что модификация алгоритма Дейкстры, в которой среди разных расстояний выбирают то, в котором последнее ребро минимально, даёт правильный ответ.
Чтобы доказать это, немного модифицируем граф. Для начала найдём кратчайшие пути из u до каждой вершины. Обозначим через di длины кратчайшего пути из u в i. После этого можем удалить некоторые рёбра. Конкретнее, мы можем удалить ребро с концами x и y и весом w если |dx - dy| ≠ w, потому что оно не содержится ни в одном кратчайшем пути, а значит не содержится и в дереве кратчайших путей. После этого можем ориентировать рёбра от вершин с меньшим d в вершину с большим (потому что веса рёбер положительны). Легко доказать, что если взять по одному входящему ребру в каждую вершину, то эти рёбра будут образовывать дерево кратчайших путей. Тогда нам достаточно взять для каждой вершины, входящее в неё ребро минимального веса. Почему? Потому что мы должны взять хотя бы по одному ребру, входящему в каждую вершину, чтобы получить связный граф. Мы не можем взять ребра с меньшим весом, чем минимальное. И если мы возьмем минимальные рёбра мы также получим дерево кратчайших путей. Так что это и есть дерево кратчайших путей с минимальным суммарным весом.
Можно заметить, что такая модификация алгоритма Дейкстры выполняет точно такие же действия.
Time complexity — 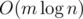










Thank you for the editorial. I ended a 4-hour contest about one and a half hour ago, and I'm not that good at greedy, so I hope I can get a better score next time...
how did u improve in greedy sir , any tips ?
I think time complexity of D is O(n log n) due to sort.
I think we don't count 'sort' in when we calculate time complexity.
on the contrary, we do count 'sort' while calculating time complexity.
thx
Thanks, fixed.
For Problem E, there is a O(m) solution by using SPFA algorithm.
Wow! Could you tell me this method?
You may read about SPFA here.
Actually, SPFA does not run in O(m) time complexity. It's just really fast on random-generated testcases, and in other special cases, it can be O(nm), the same as the original Bellman-Ford.Not a good choice on some platform which allows hacking, isn't it? :P
man, next time no 'greedy'
what is wrong with 'greedy'?
Because too much of everything is bad.. Eg me commenting too much
Can someone explain how to approach problem E ? I didn't quite get it from editorial. i.e What it means by saying where in case of equal distances we take one with shorter last edge . Thanks in advance.
Running the dijkstra's algorithm gives you a tree with minimum distances from source to any other vertex ( tree rooted at source ). Suppose this case :
Now if we have to make a choice between these two in terms of minimum distance, we can see that choosing either is fine. But in case of forming the tree with minimum weight , we need to minimise sum of edge weights. If we choose A->B and A->C , it is a valid dijkstra tree with sum of edges = 3 , whereas choosing A->B and B->C is also a valid tree with sum of edges = 2. So whenever distance is same during relaxation in dijkstra, choose the smaller edge.
Did you mean that we have to find MST here?
sorry , edited. We dont have to find the MST. Rather we have to find a spanning tree which satisfies dijkstra. If multiple trees are possible, then the one with minimum cost should be taken.
Cant you just consider the weights to be the distances between the nodes and run a normal Dijsktras on it.
It would be easier if you read my explanation above once and read up my code : 11189526 .. I have added lots of comments in the code to make it clear for everyone to understand.. Feel free to ask doubts.
A test case where normal dijkstra might fail :
1 2 1
2 3 1
1 3 2
source : 1
Here you can go from 1->3 in cost 2 , but you should select 1->2->3 instead of 1->2 and 1->3 in your tree. You can easily see that both the solutions are valid dijkstra trees.
Народ, подскажите пожалуйста, почему TLE? :)
засыл
strlen в цикле плохая идея
Зашло, спасибо, чудеса! :) Неужели strlen за линию работает? :)
похоже на то, вот уже обсуждалось
Спасибо! :)
'maked worse'?
Can anyone tell me why this solution gave WA for test 11 question C? I used DP where prev=0 means previous tree wasn't cut, prev=1 means previous tree was cut to left, prev =2 means previous tree was cut to right Solution Also I always cut the 1st tree to the left and when I am at i-th tree, I check if prev value was 0,1,2 and accordingly I move forward. And I cut the last tree to the right
Hii, in the line 47 use this : "if(p[i].first-p[i].second>p[i-1].first+p[i-1].second) x=func(i+1,1);" instead of: "if(p[i].first-p[i].second>p[i-1].first+p[i].second) x=func(i+1,1);".
Not sure... what did I do wrong here http://codeforces.me/contest/545/submission/11155373
Getting WA on 5th test case for E problem. Does someone have an idea what is wrong with my code? Or maybe I can somehow view input of 5th test case :-) ? http://codeforces.me/contest/545/submission/11175222
I've managed to get AC on problem E. But I'm still confused and don't understand one fact. These are 2 solutions:
http://codeforces.me/contest/545/submission/11195293 (WA on 5th test case)
http://codeforces.me/contest/545/submission/11195260 (AC)
The difference is only in 1 line (line #40)
vs
Can someone explain me why does its really matter?
if you don't compare v and o.v when distance is equal, vertiсes (5, 0) and (5, 1) are equal
Exactly. But why is it a problem? They will be processed both in some order
TreeSet<Vertex> qif you insert (5, 0) and after it (5, 1), it will not be added. I think you don't want such behavior
No, it seems that set will contain both because vertices are not really equal. (compareTo == 0 isn't the same as equals == true)
no
Yes, you're right :-) Thank you very much for help!
hi, can anyone explain where i went wrong for 545b problem , link is http://codeforces.me/contest/545/submission/11158712 ,,,,, what i done is ,if the no of mismatch positions are odd then cout<<"impossible" else im flipping the first half of mismatch bits of first string and displaying it.
char ...n; It's wrong. You need n up to 10^5, it should be int.
Why am I getting WA in my solution ? I have covered all possible cases seland
http://codeforces.me/contest/545/submission/11184421
Maybe this can help you:
4
1 1
2 2
6 2
7 1
The answer is 3 while your answer is 4.
I think that for this test case ,
1st tree fell left, 2nd tree fell right, 3rd — left ( it can fall left ) , 4th — right
==> all 4 fell Please check phfvtm060
Sorry , I just forgot this case
If 2nd fell right, it'll take [2, 4] and 3rd fell left, it'll take [4, 6], which overlapped 2nd. So the answer is 3.
I tried to solve the problems after the contest and is successful for three(solved one during contest) and for 545E — Paths and Trees I am getting wrong answer on test 8. Here is my source http://codeforces.me/contest/545/submission/11186979 can someone help me where does it go wrong?
I debugged and found an overflow.
Подскажите пожалуйста что не так с решением 11166029. Жадность но не работает.
"It's true, that Dijkstra modification, where in case of equal distances we take one with shorter last edge, find an answer." Why do we take the shorter last edge in case of equal distances? No matter what edge we choose, it leads to shortest distance from source to that vertex. I don't see how this affects the weight of the shortest path tree. Any test case where not choosing shorter last edge fails?
The one from problem statement with 3 vertices
there is another solution for E where u can run dijkstra on the graph from u , then sort the nodes by distances , then add each node to the tree for further details check this out 11271206
I think it is the same solution
Hi anyone can please tell me why my code is getting memory limit exceed? It passes much larger cases but get memory limit exceed in a small case! My submitted code For E. Thanks.
Found it. When only updating the smallest weight no need to push into the queue again.
Even After reading the solution I thought of implementing a solution for problem C Could not find why it is wrong. TLE ok it can come as the answer is m*n may be
submission
The strategy I have implemented is
All the students attack the problem from the front. For each block ai student remain and the rest go forward and go to the next state. If a[i]>students arrived at the spot then all the student stay and remove until a[i]<less then the students the student start to pass to the next tasks.
I got wrong answer on 4th test case but could not figure out why any help would be appreciable
For the E question cant we just add the nodes in the order the that they get popped from the priority queue as this will ensure that sum of distances is also the least. Please correct me if wrong :)
The editorial for the problem C says:
__ Also this problem can be solved by the next greedy algorithm. Let's fell leftmost tree to the left (it always doesn't make an answer worse). After that, try to fell the next tree. If we can fell it to the left, let's do it (because it also always doesn't make an answer worse). If we can't, then try to fell it to the right. If it is possible, let's do it. Last step is correct because felling some tree to the right may only prevent the next tree's fallen. So we may "exchange" one tree to another without worsing an answer.
If we follows this approach then for the following:
13
5 9
16 10
24 7
30 5
34 3
36 1
would be 3 bu isn't the correct answer 6? (Fell all trees except the second one)
number of trees = 13 . You only printed 6 of them .
Guys, I didn't understand the DP solution of problem C ... Can anyone help ?
So, the idea is that you have these three DP arrays stay, left and right and you have that:
. Finally, you answer is given by max(stayn, leftn, rightn).
I hope that was good enough for you. If not, don't hesitate to ask more questions.
Thanks a lot!
Here is my solution for Div 2 — C using Top-Down DP/Memoization. 44734044
Not able to understand why greedy is giving AC.
In case tree fall in right direction then it may cover more than 1 trees right ?. Which will lead to bad result
It cant cover more than 1 tree, because even if it is covering the coordinate of first right tree, we can't make it fall on the right (thus not counting this in our answer). In fact, it can't cover any tree. Thus at worst case, we will be taking possible left "fall" of right tree, if we make the tree fell to its right (but its ok, since at the expense of 1 right tree, we are increasing the answer by 1).
vovuh could you plz explain your DP approach of 3rd problem
There's a typo in the editorial of problem E.
"egde" -> "edge"