Good day everyone.
Every programmer occasionally, when nobody's home, turns off the lights, pours a glass of scotch, puts on some light German electronica, and opens up a file on their computer. It's a different file for every programmer. Sometimes they wrote it, sometimes they found it and knew they had to save it. They read over the lines, and weep at their beauty, then the tears turn bitter as they remember the rest of the files and the inevitable collapse of all that is good and true in the world.
This file is Good Code. It has sensible and consistent names for functions and variables. It's concise. It doesn't do anything obviously stupid. It has never had to live in the wild, or answer to a sales team. It does exactly one, mundane, specific thing, and it does it well. It was written by a single person, and never touched by another. It reads like poetry written by someone over thirty.
(excerpt from http://www.stilldrinking.org/programming-sucks)
Do you have such code? For me it's code for binary power
long bin(long x, long a) {
long y = 1;
while (a) {
if (a & 1)
y = (y * x) % mod;
x = (x * x) % mod;
a >>= 1;
}
return y;
}
and Gauss algorithms (the latter is longer than nine lines, so I don't post it here).
I'll be happy to see yours masterpieces!










Quicksort in Haskell:
Nice example, but it's not quicksort!
Names are consistent for sure.
Fast exponentiation would be one of my first choices as well along with several other pieces of code that rely on bit masks, specially DP with bit masks, for example storing all ancestors of a node of a tree that are 1 << i distant from it and then using those values to calculate lca of two nodes: That's what I call perfection, the way it all fits together.
That said since we are choosing a piece of code I would like to post the code to calculate the z function:
So fast, so beautiful and so powerful!
Though a one-liner, my favorite is the recursive implementation of Euclid's Algorithm (GCD):
int gcd(int a, int b) { return a ? gcd(b % a, a) : b; }Not recursive version
what about this
__gcd(a,b)Personally I prefer this :
gcd in python, is my favourite (from fractions module, not mine)
I like my implementations of string algorithms. For example, KMP:
Does the build_pi() function work properly for strings like "aba" or "abcde"?
Let's see. pi[i] is equal to the length of the border of the string compound by the first
icharacters ofstr.The output for "aba" is:
-1 0 0 1
and for "abcde" is:
-1 0 0 0 0 0
So I think that yes, it works properly.
My bad, I didn't notice your pi[] array uses 1-based indexing. Sorry for that.
You may consider using
~kinstead ofk >= 0.I don't understand what do you mean?
~kis a way to check if k is -1 or not. In the following code, the print statement won't be executed.In your code, as you are checking if k is -1 or greater (umm, that's what I think :D), so you may replace
k >= 0with~kif you want.(explanation: -1 contains all ones in its bit representation. So it's compliment ~(-1) contains all zeros i.e. 0. For every other numbers, they contain atleast one zero in their bit representation. So their compliment contains atleast one 1, i.e. non-zero)
Yes, you are right. I got it now. Although I think that maybe this trick is too dark in this case ;)
Actually I use it pretty much everywhere (reading till EOF, traversing edge-list, custom stacks etc) :p
Stop it.
By the way, you don't have to do the matching separately. You can create a string X = pattern + SEPARATOR + text, build the pi array for X and check which indices have pi[index] = pattern.size() :).
I like my segment tree!
Computing Euler's totient function for all natural numbers <= n in O(n*log n):
Do you know some problems on Codeforces that are solvable using this function ?
http://www.spoj.com/problems/NAJPWG/
You can make it +-4x faster (though not quite as elegant):
Thank you winger, this is really elegant code. And cost me long time to think:
Full size: http://farm8.staticflickr.com/7728/17750074264_6483e46042_b.jpg
You forgot to do Phi[i]--; after it has been used because totient of prime number n is n-1
The first iteration (with i=1) does exactly that.
Will calculation using Eratosthenes sieve be faster? Seems that it has better complexity O(n loglog n)
Sparse Table Data Structure (masterpiece)
Floyd-Warshall algorithm
Computing Modular Inverses (Modulo a Prime) for Natural Numbers <= N:
This works with primes only.
If MOD=12, inv[5] relies on inv[2], which is not specified.
Fixed, thanks. It's been too long since I've worked with MOD != 1000000007 :)
A one-liner to calculate modular inverse, returns 0 if gcd(a,m) != 1.
Path compression!
On a related note, how do I add codes in comments, with proper formatting?
Click on the second last option on the menu bar, and then click on Block. Put your code inside the tildes generated.
I prefer less readable
:)
The power of Python.
:|
My bad. :|
The power of C++.
or just
No need to create a new string:
Bogosort.
You are True God of Code Formatting
Once, my friend and I were arguing why he codes that way. The explanation we agreed upon was that he absolutely loves python-like formatting.
Reminded me of this Java snippet in Python-like style =)
https://pbs.twimg.com/media/B-hLBUFIYAAKhPN.png:large
Xellos, did you code this? :D
No, >implying I code in Java unless absolutely necessary.
Speaking of Xellos's code formatting, I would also like to know how he's come to this particular style :D
It's what fits me the most.
the image doesn't show, so here
I am wondering what is the complexity of this algorithm, maybe O(n! * n)
It's not guaranteed to finish at all. The expected time to finish should be something like n!·n, the worst-case (O-notation) is O(∞).
(assuming true random, of course)
You are right!
Except for n=1 :P
Maximum flow. (Can the code be made better?)
maybe only asymptotically
This one is a bit longer but faster than most of the implementations I've seen. (My template and a sample implementation)
What means ~ i?
This
Two pointers:
Binary search without overflow:
omg xD, so useful, much trick
If you like such nasty bits tricks take a look here: http://codeforces.me/blog/entry/13410#comment-182868
It seems that the trick with
int mid = (lo & hi) + ((lo ^ hi) >> 1);is necessary evil here. Can't invent how to correctly calc mid in a more simple way.I guess that you disregard (lo + hi) / 2 since you emphsized that this binary search is "without overflow", but can you give me a link to at least one problem, when you needed to handle numbers bigger than 263, so adding such numbers will cause overflow, even when using unsigned long long? I guess no, and even if there are such problems I think that lo / 2 + hi / 2 + (lo&hi&1) is simpler.
lo / 2 + hi / 2 + (lo&hi&1)doesn't work for negative values. If lo=-3, hi=-1, result is 0 (instead of -2).Ehhhh... Playing with bits of negative numbers is something like dancing on the edge of canyon. That whole discussion is so utterly nonsense. Is this a REAL problem? If problemsetter is such an asshole that two times range overflows unsigned long long then he could as well demand bignums >_>.
Taking care about not doubling the range is something extremely not important in my opinion, I would be more interested in not doubling the EXPONENT of range in geometry.
The discussion turned out to be unfair because I initially thought about library implementation of binary search (which must work correctly for any legal input).
I agree that solving a contest problem it is usually enough to merely use 64-bit integer if there is a risk of overflow.
I've always thought
mid = lo + (hi - lo) / 2does the thing. What's the downside of such operation?If
lo = -2e9,hi = 2e9thenhi-lowoverflows.lo + ((hi - lo) >>> 1)works fine in java.Nice solution.
I use this approach instead:
Overflow stuff: it's usually better to use long longs where appropriate (with rules like "a computation that uses long longs doesn't return int"), not initialise anything to too big constants and not bother with details.
Take a Look at his codes -> Archon.JK
Seeing many binary searches here I will put mine, which is in my opinion much more clear and safe. Everybody knows that binary search is extremely prone to mistakes, especially for beginners, so here's my completely invulnerable to any mistakes approach.
What's so special?
First reason: I keep an invariant that interval [kl, kp] is something I don't know anything about. Stop condition is obvious — that interval is nonempty <=> (kl <= kp). Many people try to keep an invariant as sth like "I know that first element of my interval is good, about others I don't know" or "I know that first element is good, last is bad, rest unknown", but in my opinon this is much more complicated to maintain and demand much more thought about when to end this (look at this lo < hi - 1 in Xellos' code :<). Another kind of problems it omits are all about initialization, it may be also troublesome to those solutions with invariants other than mine.
Second reason: It's invulnerable to any bugs like "if beginning is odd, end is even and checked value is not good, then blah, blah and I will end up in infinite loop" or "if beginning is negative, end is positive, then stupid division of negative numbers will cause rounding in bad side, so blahblah, infinite loop". I got those +1 and -1 in case of success or failure, so my search interval is clearly strictly shrinking, no matter what, being even/odd/positive/negative is of no relevance.
omg, and you say it's easier to maintain then f(l) = true, f(r) = false ?
And am I right that you have to carefully choose res for the case where test is never returns true?
OK, I agree that maintaining f(l) = true, f(r) = false is equally easy (don't tell me that's my way is not easy), HOWEVER... How do you initialize your boundaries so that f(l) = true and f(r) = false? Another advantage is that kl <= (kl + kp) / 2 <= kp, no matter what, so I always check something that I have not checked so far. If my invariant was f(l) = true, f(r) = false, then what I have to be sure is that (l + r) / 2 lies inside [l+1, r-1] interval. That may also be true, but surely it demands a long thought about all possible parities, about positivity/negativity and about careful stop conditions. I don't have any of those problems.
In case when test never returns true I have res = -1 (or any other value not inside a starting interval), so it's trivial to handle this. In both indy's and Xellos' binary searches it is impossible to tell cases when test never returns true and if smallest value that test returns true is largest value in interval. However, indy handled it well since he named that largest value "toExclusive" (and probably Xellos handles it well also, but it can't be seen in that piece of code), but that's another thing to take care about, to remember that this value must be larger, in Xellos code that's at least nice symmetry, indy used "closed-open" concept which I personally hate and it makes it completely nonsymetrically between cases.
Well, (l+r)/2 is always inside a range in my code too(if I haven't finished)
Yes, sometimes it may be a bit tricky to get correct l,r if you do it for first time, but in general I would say, if you know how to write if for your -1, then you know how to write correct start condition
In contest problems I use the following symmetric version:
It is not obvious to check for correctness, but at least this version is highly symmetric and is similar to binary search in real domain:
Then look at this kl = cur + 1 and kp = cur - 1 in Swistakk's code (two more +-1s) :D
Whatever, man. As long as one doesn't mix up the boundaries of the interval, the rest is clear and easy to understand. It's just binary search, mistakes there are for noobs.
I should dig out my FFT and put it here — master trole.
I don't understand why you get some downvotes. This is also EXACTLY how I always code binary search, and I also believe that this is the most intuitive way.
Whenever I see someone write
left = midorright = mid, I am confused as how to make sure that this thing terminate correctly. It's even worse when people avoid creating new variable res and returnleftorrightat the end. I don't understand why people spend extra time to deal with all these complications to make it work, while it could be so simple & beautiful.Convex hull in O(n*log(n)) in Python:
calculate n-th Fibonacchi number (possibly modulo something) in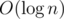
Reading single integer from input:
This actually made me laugh :D :D
Recursive Fenwick-Tree masterpiece [Please read the sentence with a proper British accent!]
Z- and prefix- functions, maybe :)
Some short code
in Java
It seems that second example is undefined behavior, because (as far as I understand) order of evaluation of
a + band(b = a)is not specified.the swap function can be like this:
This code causes undefined behaviour.
Yeah, I wasn't sure about it. I wrote it because it runs fine on CF and my machine.
Counterexample
Computing inverse modulo MOD for all natural numbers < MOD in O(n):
My favourite is implicit cartesian tree: http://pastebin.com/8fhVg3r4
my bad..
I like many many many algorithms and functions. One that comes to mind now is inclusion-exclusion principle, which I used quite recently, which can be beautifully coded in one line.
Code computing zeta and mi transformations (zeta(mi) = mi(zeta) = Id) — look at explanation here: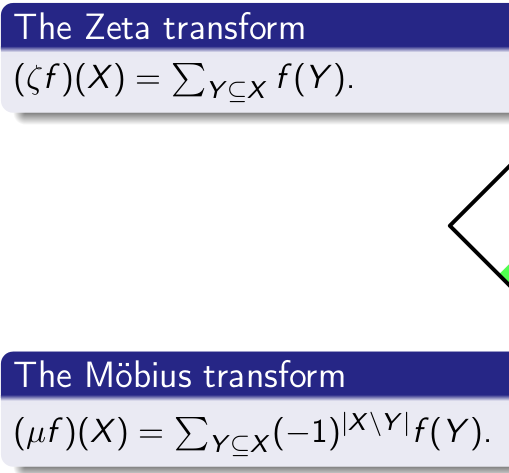
sign = 1 for zeta and sign = -1 for mi :)
Even since I learned about it, I've always been captivated by the magic of DSU.
I like this implementation of Burunduk1.
Returns next integer in input.
Check if a number is even:
~x & 1More readable version:
x%2==0You reminded me or this :p
Here's a piece of code that does some magic. Can you find out what it is? The input is a sequence V of nonnegative integers.
Something weird and absolutely wrong is in Rev. 1.
Spoilers in first edit.
Precisely (including your remark in parentheses). Good job! :)
My guess in rev1
Binary search
Quickly! Downvote it as fast as you can — the sooner we make it hidden the less people will see this and will code like that!
What is happening to me ? :'(
Malbolge is a language deisgned to be the worst ever.
Apparently, it failed.
Opps, some one added it before :P
http://goo.gl/C9QIhH
Thanks! Updated the function names :P
с[i]— i-th Catalan number modulomodHow often do you use Catalan's numbers?
Kruskal algorithm with DSU.
Considering the power of Python... I like my solution of Timus 1067
Well, the part with
reduce, maybe, is not perfectly readable, but the main trick isrecursive_defauldict.