544A - Набор строк
В этой задаче нужно написать то, что написано в условии. Для этого можно воспользоваться массивом, с помощью которого мы будем понимать встречалась буква до этого. Будем будем обрабатывать символы по очереди. И поддерживать некоторую строчку. Если текущий символ ещё не встречался, то тогда начнём новую строку, а текущую строку мы положим в массив ответа. Иначе добавим текущий символ конец текущей строки.
Если в массиве ответа окажется больше чем к строк, то тогда сконкатенируем на несколько последних в одну.
Авторское решение: 11035685
544B - Море и острова
В эти задачи нетрудно понять что оптимальный ответ всегда состоит из одиночных клеток обладающих следущим свойством: сумма индекса строчки и столбца четная. Таким образом попробуем разместить ровно k островков в этих в клетках, если не получится, то ответ на задачу NO. Попробуйте доказать почему всегда так действовать оптимально.
Авторское решение: 11035691
543A - Пишем код
Давайте для начала придумаем решение который будет работать медленнее чем нужно. Будем решать задачи динамическим программированием: z[i][j][k] — мы обработали ровно i программистов, написали ровно j строчек кода и при этом возникло ровно k ошибок. Как сделать в такой динамике переходы? Очень просто, переберём сколько строчек напишет i программист (пусть r) и прибавим к z[i][j][k] значение z[i][j - r][k - r[ai]]. Однако давайте посмотрим на переходы с другой стороны. Очевидно, что i программист либо не напишет ни одной строчки, тогда к ответу прибавится значение z[i - 1][j][k], либо он напишет одну строчку, а остальные строчки учтутся в значении z[i][j - 1][k - a[i]]. Здесь можно провести аналогию c подсчетом биномиальных коэффициентов c помощью треугольника паскаля. Таким образом получим решение за ассимптотику O(n3)
Авторское решение: 11035704
543B - Разрушение дорог
Для начала попробуем решить задачу проще: задана пара вершин, нужно определить минимальный набор ребер, который нужно оставить, чтобы существовал путь из одной вершины, в другую. Очевидно, это число в точности равно кратчайшему расстоянию между вершинами.
Теперь перейдем к искомой задаче. Пусть d[i][j] — кратчайшее расстояние между вершинами. Такую матрицу очень просто насчитать, запустив из каждой из n вершин bfs. Отлично
Теперь разберем два случая: Пути не пересекаются, тогда ответ можно обновить числом m - d[s1][t1] - d[s2][t2] (при условии, что выполнены условия на длину путей). Иначе, заметим что если пути пересекаются, то тогда тогда ответ имеет вид буквы Н. Более формально, сначала каждый из путей будет содержать различные ребра, потом несколько общих ребер, идущих подряд, и затем каждый из путей будет содержать различные ребра. Таким образом, переберем первую и последнюю общие вершины пути. Пусть эти величины равны (i, j). Тогда обновим ответ величиной m - d[s1][i] - d[i][j] - d[j][t1] - d[s2][i] - d[j][t2] (при условии, что выполняются ограничения на длину путей). Стоит отметить, что также стоит обменять вершины s1 и t1 местами, и снова обновить ответ, поскольку иногда выгодно соединить t1 и с вершиной i, а s1 с вершиной j. Решения, которые не учитывали это не проходили 11 тест
Авторское решение: 11035716
543C - Запоминаем строки
Во первых стоит отметить важный факт: количество строк меньше длины алфавита. Таким образом, всегда когда мы хотим сделать замену символа на другой, мы всегда сможем найти подходящий другой символ.
Далее возможны две ситуации: за одну операцию мы можем взять и заменить символ на любой другой, за это мы заплатим a[i][j] денег ( в зависимости от столбца, в котором мы сделаем строку уникальной). Либо за мы можем взять некоторый столбец, и рассмотреть некоторое множество строк, имеющих одинаковый символ в заданном столбце, и все сделать их уникальными. За это мы оплатим стоимость замены всех символов, кроме одного: самого дорого. Таким образом, получим решение: d[mask] — ответ на задачу, если мы сделали все строки, отвечающие за единичные биты уникальными. Как пересчитывать такую динамику? Пусть lowbit — младший единичный бит. Тогда очевидно, что мы сделаем его уникальным либо с помощью первой операции, либо с помощью второй. Для этого, переберем столбец и рассмотрим множество строк, имеющих такой же символ с со строкой lowbit. И обновим ответ соответствующим значением. Получим решение за ассимптотику O(m2n), где m — длина строки.
Авторское решение: 11035719
543D - Улучшение дорог
Подвесим дерево за вершину 1. Для начала подсчитаем вспомогательную динамику d[i] — количество способов починить дороги для поддерева с корнем в вершине i. Как такую динамику пересчитывать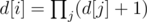 
— где j это дети вершины i. Отлично. Таким образом ответ на задачу для вершины 1 — это d[1] Далее научимся переподвешивать дерево за некоторого ребенка j текущей вершины i. Очевидно, пересчитаем величину d[i]: suf[i][j] * pref[i][j] * d[parent], где parent — это родитель вершины i, (для вершины 1 d[parent] = 1), а массивы suf[i][j] — это произведение величин d[k], для всех детей i, k < j (pref[i][j] — k > j). После этого, обновим значение d[j] значением d[j] * (d[i] + 1). Все, теперь вершина j стала корнем, и ответ для нее — текущее значение d[j]
Авторское решение: 11035737
543E - Слушаем музыку
Отсортируем песни по убыванию. Будем последовательно рассматривать песни и говорить, что теперь песня хорошая и удовлетворяет критерию качества. Пусть si = 0, если песня с номером i еще не добавлена в рассмотрение, и si = 1 иначе. Тогда пусть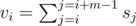 
. Очевидно, когда мы добавляем новую песню позиции idx в рассмотрение, мы должны сделать + = 1 на отрезке [max(0, idx - m + 1), idx] в нашем массиве v. Значит, чтобы ответить на запрос, мы должны поддержать структуру данных которая могла бы восстановить заданные значения в массиве v в на тот момент, когда все песни имели качество ≥ q. Кроме этого, она должна использовать мало памяти. В итоге ответ на запрос очевидно равен m - max(vi), lj ≤ i ≤ rj.
Каждые 
добавлений песен сохраним три величины: значение первого элемента в блоке позиций, максимум значения массива v на блоке, и дополнительно не более обновлений, которые пришли в текущем блоке обновлений, но не покрывали полностью заданный блок. Используя эти значения нужно аккуратно восстановить нужную информацию о массиве v и ответить на запрос.
Авторское решение: 11035739
А что случилось с задачей Е?
Разбор к ней будет написан в ближайшее время
В решении задачи B можно для соответствия условию заменить индексы на (s_0, t_0), (s_1, t_1) -> (s_1, t_1), (s_2, t_2).
Можно, конечно. Только я предпочитаю обсуждать подобное через личные сообщения: "Пост исправится, а коммент останется"
Впредь учту
I think in part
543A - Writing Code,fourth lineshoud bez[i][j][k] value z[i - 1][j - r][k - ra[i]]not canz[i][j][k] value z[i][j - r][k - ra[i]].I still don't understand about
The second case, is to give at least one task to i-th programmer.So, this value will be included in that state: z[i][j - 1][k - a[i]]. In that solution we use sameidea, which is used to calculate binomial coefficients using Pascal's triangle..Can you explain clearly for me. Thanks !
Sorry for my bad English
Ok, we have current state z[i][j][k]. we perform transitions, first z[i + 1][j][k] + = z[i][j][k], second z[i + 1][j + 1][k + a[i]] and so on. You can see, that when we calculate value z[i + 1][j + 1][k + a[i]] we already have z[i][j][k] in state z[i + 1][j][k].
[EDIT]: I had a huge misconception. I created a blog for this question. Hopefully this will help. Let's call a sequence of non-negative integers v1, v2, ..., vn a plan, if v1 + v2 + ... + vn = m.
can v1, v2, ..., vn be zero? sorry I got confused because of example input 3. as the answer is 0.
Yes, "non-negative integers" means any number >= 0.
yes, any of v1, v2, ..., vn can be zero.
Same thing using the recursive formula:
= dp(i, j - 1, k) + dp(i - 1, 0, k - jai)
English Version plss . Translator works badly for eg for Div1C .
On 543D, I don't understand why
For each children of i, the states of roads between i and any child are independent of each other, so d[i] is the product of them.
For problem B, "Let's come back to initial task. Let's d[i][j] — shortest distance between i and j. You can calculate such matrix using bfs from each vertex. ", so the complexity is O(n*E), and E may be n*(n-1)/2, so the complexity in worst situation is O(n^3), why it can be figure out in 2 seconds? Or the test data is weak?
notice that: E <= min(3000, n(n-1)/2)
oops, I'm silly, I found the solution in the contest time, but I have not writen it, because I was under the misapprehension that E maybe reach n(n-1)/2.
although i fail to solve anyone in the contest, but i still think the problem is very good. Thank you!
Failed C WA #11 but have the same idea as you and fell from 16th to 140th place because this in first contest :( :( :(
I want ask can't paths in D intersect more times not just once?
For 544A, I am getting the correct output but the Checker log says wrong answer s_1 + s_2 + .. + s_k != q. I know it is trivial but do help me understand.Submission 11025841
I resubmitted your exact code and it got Accepted. So I don't get why your code didn't get Accepted the first time around.
Would anyone please discuss the recursive dp approach to DIV 2 C ?
In editorial solution of
DIV 2 C, why we are taking the arraydp[2][N][N]? As there are i people shouldn't it bedp[N][N][N](which will cause memory limit though) ? What's the trick behind this implementation ?To compute dp[i][][], you only need values from dp[i-1][][]. So you only maintain 2 positions (current and previous).
In 543 B why is it necessary that we have to consider the shortest paths only ? Can't there be a case where there are two paths that intersect to an extent that the number of edges on these paths is lesser than the edges on the shortest paths in cases where the shortest paths dont intersect at all ?
Like for example if shortest path from s1 to t1 has 4 edges and that from s2 to t2 has 4 edges as well but they dont intersect so we can destroy m-8 edges but what if there is another path from s1 to t1 which has 5 edges and also from s2 to t2 which has 5 edges and 3 of these 5 edges are common. So total distinct edges will be 5+5-3=7 and we can destroy m-7 roads which is better than m-8.
Sorry for the long post but it would be great if someone could clear this for me :p
In the intersecting case, you don't have to find the shortest path from s1 to t1 and from s2 to t2 and then remove the common edges. Consider a H-shape with the horizontal line as common path with end points p1 and p2. You need to consider shortest distances from s1 to p1 (upper left vertical line), s2 to p1 (lower left vertical line), p1 to p2 (horizontal line — representing common path), p2 to t1 (upper right vertical line) and p2 to t2 (lower right horizontal line).
Ok seems like I misunderstood then. Thanks.
Can someone please explain 543A? I understood it using 2D dp solution 2D DP but dont understand what is given in the tutorial. How are you making the recursion?
I created a blog. Hopefully this will help.
problem e is clearly google translated, its hard to understand anything from it
div1.A can be solved by two dimension complete_knapsack.
I can't agree more
In 543 B, why are we swapping only s0,t0? Shouldn't we swap s1,t1 too and check for that case?
got it.
OK You got it, can you tell me why?
For Div1 — D, the statement said:
"Next line contains n - 1 positive integers p2, p3, p4, ..., pn (1 ≤ pi ≤ i - 1) — the description of the roads in the country."
But I didn't see anything talk about this before. So, what do these numbers mean?
Please explain more clearly. I understand the rough idea, I don't understand what you store and how you recover v.
If I understood it right: You store O(sqrt(n)) memory after every O(sqrt(n)) added songs, for O(n) memory in total. To answer a query, you go to the last stored point before the corresponding q_i, then add O(sqrt(n)) songs after that point. At every stored point, you store: The first v of each block, the maximum v of each block, and "about sqrt(n) of small updates which doesn't cover full block". What do you mean by the small updates? Which ones, and how do you store them? How do you answer the query using that?
Let's suppose that we have an query [li, ri]. First, we can notice, that li sometimes is not a start of some block. In that case, let's use value vj, where j — is first element of same block with element i. We need update value vj with no more then
updates, after that we can get original value vi using array with quality — a. Same thing we can do with ri, if ri is not a finish of some block. After that, we will have only full blocks. First thing, that we need to do, we need to apply ''small'' updates, for some blocks. For example, we have block [0, 50], then ''big'' update will update full block, and small only some part, [1, 4], [0, 20], [1, 50]. This updates we have when some updates doesn't cover full block. After that, let's process few queries [lk, rk] and full blocks, that this blocks cover. We can not do this in naive manner, but we use following trick: let's g is a first full block that is covered but query and f is last. We will do push[g] + = 1 and push[f + 1] - = 1 and after that we need to calculate partial sums here. So, now we can answer to query on such blocks. Is it clear now?
We have a slight language barrier, but we're making progress. Sorry that some people downvoted you for that.
If l_i is not the start of a block, you use O(sqrt(n)) brute force to make it the start of a block, same for r_i. Understood.
For each update, updating the blocks that are fully covered is easy, just use prefix sums. Got it.
But what do you do about the updates that don't start at the beginning of a block? You don't even store all v values inside a block, so how do you do this update?
General idea — is to separate updates that fully cover some block, and ''small'' updates that doesn't cover full block. In first case we process such updates using prefix sums when we need to answer the query, and ''small'' updates we can process in naive way, and after that keep only maximal value after update for block.
What do you mean by naive way?
You don't store all values of v, so how can you update them?
EDIT: Nevermind, got it. You don't just start a new block after every sqrt(n) indices, you also start one whenever an update starts or ends. So 3*sqrt(n) blocks in total for each stored point.
Thanks for the patience.
Would you be so kind and answer following question: why it is sufficient to store O(sqrt(n)) information at each store point? How it is possible to restore information inside the block using the stored information?
A single store point is responsible for the queries with qi in some interval [a,b], such that the interval [a,b) contains O(sqrt(n)) songs (it doesn't matter how many songs have value b). For this store point, we partition the v array (which contains information about all songs with value in [b,infinity) ) into blocks with the following properties:
First property: For every song i with a_i in [a,b], a new block starts at i and at i+m.
Second property: For each k, a new block starts at k*sqrt(n).
These two properties can be satisfied with O(sqrt(n)) blocks, since k is between 0 and sqrt(n), and there are O(sqrt(n)) songs with a_i in [a,b). For each block, we store the first, last and best v_i inside that block (so 3 values per block).
The two properties guarantee that we need O(sqrt(n)) time per query: The second property makes sure the start of a block is always nearby, and the first property makes sure that we have enough information to process all songs between the store point and the query point in O(1) time each (that's O(sqrt(n)) songs with O(1) time for each song).
Restoring the information works, because each song covers only complete blocks (first property), not any partial block. So, the first, last and best v of a block are all increased by 1 when you add a new song that affects that block. The first and last let you convert the query so it starts where a block starts and ends where a block ends, while the best lets you process each block in O(1).
But what do you do if li=j is inside any block? You have to restore (find maximum) from vj, vj+1, ... , vj+O(sqrt(n)). Do we use array of qualities? How? Thank you.
Update. Looks like this: We have v1 and we can go from vi to vi+1 in O(1) using quality array. Thank you.
We don't have just v_1, we have v_i if i is the start of a block (so distance at most sqrt(n) from j).
I think my algorithm for problem D (Div.1) is correct but get wrong on test 10 :((
Who can help me ?
CODE
sorry for bad English:|
It seems that you are using division by 0 modulo P somewhere, and result isn't correct in this case.
tanks a lot!:)
How to fix it?
Present any number x as pair < x / Pα, α > , where α is maximal degree such that x is divisible by Pα. So, 1 = < 1, 0 > and 2P3 = < 2, 3 > .
tanks!
In this problem, you just can calculate prefix and suffix product
thank you so much. and I will try to learn more about prefix and suffix product.
Hi. Do you know that a / b = a * inv(b) mod p if gcd(b,p) = 1? Are you sure that the condition gcd(b,p) = 1 is satisfied in your solution?
There's some misunderstanding. If p is prime and b % p != 0, a/b=a*b^(p-2) If p is prime and gcd(b, p) == 1, b % p != 0. So, there isn't any problem.
I'll give you an example.
a = 24; b = 6; p = 3; inv(b) mod p = b ^ (p - 2) mod p = 6 mod 3 = 0;(a / b) mod p = 1(a * inv(b)) mod p = 0 != 1So as you can see the requirement of b and p being coprime is important here.
0 / 0. Good example.
0/0? Are you serious?:) I didn't write it like
a / (b mod p)as you can see, which is absolutely different example.I suggest that you look here where it's clearly stated.
Can someone help me optimize this code? http://codeforces.me/contest/542/submission/11055397 I essentially just implemented the solution given in the editorial, but it runs in about 2.3 seconds.. I tried some small optimiziations you can see in my submission history but to no avail (the answer is printed but still shows TLE)
You could try doing this
I tried this (and the below suggestions) and now the code runs in 1.7 seconds on my machine but still gives TLE ?!?!?!!? why is this happening? (this is my new code http://codeforces.me/contest/542/submission/11066406)
http://codeforces.me/contest/542/submission/11056795 The most of the time takes the last cycle. You should precalculate pows.
Or better:
http://codeforces.me/contest/542/submission/11056795
What a great editorial for 544B:
It starts off by saying: "It's clear to understand". If it's clear then what are editorials for, you idiot? IF SOMEONE IS READING THE EDITORIAL, IT MEANS THAT IT IS NOT CLEAR TO THEM. IF IT WAS CLEAR THEY WOULD NOT BE READING THE EDITORIAL, YOU DUMB ASS. Then it gives the answer in one line without explaining AT ALL how to reach the answer. And in the end, instead of giving the proof it says: "Try to prove that this solution is optimal." TRY TO PROVE THAT IT IS OPTIMAL?? THEN WHAT THE HELL IS THE EDITORIAL FOR?
WHY DO YOU EVEN BOTHER TO WRITE THESE 2-3 LINES? WHY NOT SAY GO FIGURE IT OUT YOURSELF. At least you can be honest then, instead of writing this fake ass editorial.
You made my day man (LOOOOOL)
In 544B why do we get wrong answer if we place Land(L) on cells whose sum of row and column is ODD, instead of EVEN?
For example, you need to place 5 islands on 3x3 land. So the only answer is this
LSL SLS LSL
If we try to place land when (i+j) is odd, then the most we can get is
SLS LSL SLS
so this way we can only place 4 islands.
What's the time complexity of 543E
Does anyone know a similar task to 543A — Writing Code?
In problem B case 2 , why is taking only H shaped paths optimal not paths having some common path and then uncommon and then common ...?? Please do answer anyone!!
sorry to say, but i really dislike tutorials on Codeforces in general as usual they are very short and all i see is brief idea. 5 line of div1 D problem seems very far from enough. is it to hard to explain problem with more details like on Topcoder?. for me i can't understand well 543D div1 problem,it is not simple problem for me.i am glad, if someone can to explain it with more detail.thanks
Hopefully you are still lurking around this post after six weeks, here is a zero to one hundred explanation of Div1D.
First of all, let's simplify the problem. What if we are trying to solve the problem for a fixed capital X? Consider a dp[node][bad_road_cnt] array for processing the answer. It is not hard to see that dp[node][0] is always 1, because there is only one way to fix all the roads. For dp[node][1], there are two ways to reach this state. 1: dp[child][0] ways, we leave the road from child to node bad; 2: dp[child][1] ways, we fix the road from child to node. It is not hard to see it is unnecessary to keep dp[node][0] to calculate dp[node][1], so we will just keep a dp[node] for simple purpose.
It's not hard to see the ways of dp[node] for a subtree of nodes is the (dp[child1]+1) * (dp[child2]+1) ... of all children (Remember dp[node][0]=1). By recursion we can see that we can solve the subtrees one by one until we reach the node.
Now we can solve the problem for a fixed capital x, and that will take us O(n) time. Obviously if we stop from here we will need O(n^2) time to solve the original problem, so we still have to work better.
(The following is not the same approach as the editorial)
Consider moving the root from u to v, the only difference between the original and the new tree is that v is no longer u's child and u is v's child. Obviously we can just take away node v from dp[u] by multiplying (dp[v])^-1 = MOD, and then update dp[v] by multiplying (dp[u]+1) since it is now a parent of v.
The last thing we have to handle is zero problems. Check the comment below to learn more about it.
My implementation on 543D: http://codeforces.me/contest/543/submission/19879959
For those who are not familiar with prefix/suffix product, or doesn't have a clear visualized picture of what the prefix/suffix product is doing (just like me), here's a method using the Fermat's little theorem.
When moving the root from vertex u to v, we can simply transfer the state by d[u]*=(inverse(d[v])), d[v]*=(d[u]+1). The only problem that this method has is it is vulnerable to zero modules (Since MOD-1 is not a prime, that means we run a risk that we compute an incorrect inverse(d[v]) ).
Fortunately this is the only exception we have to handle, just keep a zero flag when handling d[u]. Whether a node where it's actual value + 1 == MOD is handled, just manipulate the zero flag of it before further calculating the value of it.
Instead of d[u]*=(inverse(d[v])) why you are not doing d[u]*=(inverse(d[v]+1)) ?? As while multiplying when v was a children of u then also for calculation of d[u] you have multiplied (d[v]+1).
I am doing dp[u] *= d[v]^-1, the brackets just juked you. :P
I m saying when v was a child of u for calculating dp[u] you have multiplied with a factor (dp[v]+1) now as you are shifting from u to v i.e making u as a child of v then to nullify the effect of vertex v on u previously why you are dividing it by (dp[v]) only instead of (dp[v]+1) ??
In function move(u, v):
pwr( (zero[v]?0:dp[v]) +1, MOD-2)
Sorry for the typo in the reply, instead of dp[v]^-1 it was (dp[v]+1)^-1
What does zero modules mean in here? Could you elaborate " (Since MOD-1 is not a prime, that means we run a risk that we compute an incorrect inverse(d[v]) "?
There exists cases where d[x] = 0 mod (MOD-1) since (MOD-1) = 2*500000003, and 0^-1 mod (MOD-1) does not exist, therefore we need to hardcode to handle this case.
Can you help?
Div1 D
Why this code got WA5, but this code got AC?!
Mystic...
Division 1 — Problem D: I will appreciate if someone can let me know why I am getting TLE for this submission: http://codeforces.me/contest/543/submission/37541129
I use DP, and I assign an index to each edge in the tree. There can be at most O(n) edges in the tree. Therefore, I would need O(n) in total. I am guessing maybe the recursive function goes in depth too much, and it causes TLE. However, I see that Judge's solution also uses a recursive function for DFS.
I figured out that when we are given a star, the recursive function turns out to be slower than I expected. This is because there are n queries, and the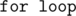
inside the recursive function can be called n times. This would yield O(n2) which definitely leads to TLE. I should have been careful about the 
in my recursive function.
[Deleted]
for problem 543B — Destroying Roads in worst case complexity is O(n^3) should get TLE but in dataset number of edges is nearly n so solution passed within bounded timelimit
For 543D, why can't you implement rerooting by multiplying dp[vertex] by the inverse of (dp[child] + 1) then multiply dp[child] by (dp[vertex] + 1)?
There's an alternative solution to problem D. So the main idea is again to do tree DP on the subtrees. $$$sub[x]$$$ is the number of ways to formulate it such that there's at most one bad road from any node in the subtree of $$$x$$$ to the "root" node $$$x$$$. There's a nice recurrence relation for $$$sub[x]$$$, namely: $$$sub[x] = \prod_{i \in \text{children}[x]} sub[i] + 1.$$$
Let's look child by child. We could have a bad edge from the "root" node to one of its children, in which case there is 1 way to proceed for that child's subtree. Or we can have a good edge from the root to the child, in which case it's just $$$sub[i]$$$. Take the product because they're independent events (one child doesn't affect the other).
The problem now is how to recompute the various values in $$$sub$$$. Good thing is that $$$sub$$$ actually doesn't change much. If we re-root the tree from $$$y$$$ to $$$x$$$, where $$$x$$$ and $$$y$$$ are adjacent, the only values that change are $$$sub[x]$$$ and $$$sub[y]$$$. They can be recomputed fairly easily too: $$$sub[y] = (sub[x] + 1)^{-1} \cdot sub[y]$$$ and $$$sub[y] = (sub[x] + 1) \cdot sub[y]$$$.
All done? Nope. There's a subtlety I missed, causing a wrong answer on the 10th test case. The issue is that if $$$sub[x] = MOD - 1$$$, then we have a 0 inverse. This doesn't happen too often, so when it does happen, all we have to do is recompute $$$sub[y]$$$ manually as $$$\prod_{i: adj[y], i \ne x} sub[i] + 1.$$$
Footnote: If we have small modulo (which we don't thankfully), my solution won't work, since we're going to have too many collisions.
Bullsh!t editorial of Div1A