Задача A. Чат
Задача решается жадным алгоритмом. Сначала найдём в строке первую букву ('h"). Далее - найдём следующую после неё букву 'e'. Если мы таким образом нашли все буквы, то ответ, очевидно, YES. Теперь давайте докажем, что если ответ был, то он обязательно найдётся. В самом деле, пусть был какой-то ответ. Посмотрим на позицию буквы 'h'. Если мы её сдвинем до самой первой влево (той, которую найдёт жадник), то ничего не изменится. Аналогично поступим со второй и следующими буквами.
Получили жадный алгоритм, работающий за O(n), где n - длина входа.
Получили жадный алгоритм, работающий за O(n), где n - длина входа.
Задача B. Монеты
В этой задаче правильным решением опять же является жадный алгоритм. Выглядит он так: перебираем все числа от 2 и далее, пока стоимость последней добавленной монеты делится на него, делим, добавляем в ответ.
Доказать корректность можно, если посмотреть на стоимости монет в разложении на простые множители. В каждой следующей стоимости все простые входят в меньшей либо равной степени, нежели в текущей (это равносильно тому, что одно делится на другое). Также очевидно, что если суммарная степень уменьшилась хотя бы на два (например, было число a = x· y· z (где y, z > 1, а стало b = x, то можно добавить еще одну промежуточную стоимость a > c = x· y > b. Таким образом, в правильном ответе сумма степеней вхождений при переходе от стоимости к следующей и меньшей уменьшается каждый раз на один. Наш жадный алгоритм именно так и поступает.
Доказать корректность можно, если посмотреть на стоимости монет в разложении на простые множители. В каждой следующей стоимости все простые входят в меньшей либо равной степени, нежели в текущей (это равносильно тому, что одно делится на другое). Также очевидно, что если суммарная степень уменьшилась хотя бы на два (например, было число a = x· y· z (где y, z > 1, а стало b = x, то можно добавить еще одну промежуточную стоимость a > c = x· y > b. Таким образом, в правильном ответе сумма степеней вхождений при переходе от стоимости к следующей и меньшей уменьшается каждый раз на один. Наш жадный алгоритм именно так и поступает.
Задача C. Деревья
Первая мысль - красивая последовательность полностью задаётся любым своим членом. Следующая мысль: хотя бы одно дерево мы трогать не будем. Доказательство: скажем, что мы не трогаем первое дерево, а высоты остальных подгоним. Они, очевидно, все будут положительны.
Решение за квадрат: перебираем, какое дерево мы не трогаем, узнаём первый член последовательности, смотрим, сколько деревьев не совпало.
Это оптимизируется до решения за линию: если мы не трогаем какое-то дерево, то у нас фиксирован первый член последовательности. Давайте подсчитаем для каждого возможного первого члена, скольки деревьям он подходит. Это делается линейным проходом по всем деревьям и операцией "инкремент" на массиве. После чего осталось найти значение первого члена, которому удовлетворяет наибольшее количетсво деревьев, и вывести n - x, где x - это значение.
Решение за квадрат: перебираем, какое дерево мы не трогаем, узнаём первый член последовательности, смотрим, сколько деревьев не совпало.
Это оптимизируется до решения за линию: если мы не трогаем какое-то дерево, то у нас фиксирован первый член последовательности. Давайте подсчитаем для каждого возможного первого члена, скольки деревьям он подходит. Это делается линейным проходом по всем деревьям и операцией "инкремент" на массиве. После чего осталось найти значение первого члена, которому удовлетворяет наибольшее количетсво деревьев, и вывести n - x, где x - это значение.
Задача D. Календарь
Для начала заметим, что так как все строки календаря должны иметь одинаковую длину, то мы легко может эту длину найти. Это просто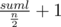 
, где suml - суммарная длина всех строк. Теперь посмотрим на строку, которую поставим самой первой. Очевидно, выгодно брать строку, чтобы s + d было минимально (где s - наша строка, а d - дописываемый символ). Понятно, что такая найдётся однозначно, иначе получается, что две строки совпадают (так как символ d нигде не встречается). Разумеется, нельзя забывать, что зафиксировав первую строку, мы зафиксируем длину второй - надо, чтобы хотя бы одна была. Отлично, с первой строкой мы определились. Теперь мы знаем длину второй строки. Здесь нам надо взять просто минимальную строку соответствующей длины (одна префиксом другой быть не может - длины равны). Таким образом, заполняем календарь по линиям.
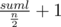, где suml - суммарная длина всех строк. Теперь посмотрим на строку, которую поставим самой первой. Очевидно, выгодно брать строку, чтобы s + d было минимально (где s - наша строка, а d - дописываемый символ). Понятно, что такая найдётся однозначно, иначе получается, что две строки совпадают (так как символ d нигде не встречается). Разумеется, нельзя забывать, что зафиксировав первую строку, мы зафиксируем длину второй - надо, чтобы хотя бы одна была. Отлично, с первой строкой мы определились. Теперь мы знаем длину второй строки. Здесь нам надо взять просто минимальную строку соответствующей длины (одна префиксом другой быть не может - длины равны). Таким образом, заполняем календарь по линиям.Задача E. Выражение
Under construction. Основная идея - кубическая динамика с переходом за 102.
I hope you complete this with write part E , good luck man :D
Good Job Man
And necroposting is not a good job
Can anyone give ideas about the DP solution for E.
I'm 8 years late, but 58C - Деревья has weak testcases. some solutions pass although they allow some tree heights to become non positive.
Case:
101 1 1 2 3 3 2 1 1 1Answer should be 8, (correct sequence:
1 2 3 4 5 5 4 3 2 1)Wrong answer is 4, (Assumes the correct sequence is:
-1 0 1 2 3 3 2 1 0 -1)Wrong submission: 51244937
Correct submission: 51245002
So when we can get the solution of E?
.
There's an another solution for C. We can notice that for the first half of the elements, if we subtract its index from the value, the values being the same is equivalent to the beautiful sequence. For the second half, the same value should be obtained when adding (index — n + 1) to the values. That value is equal to a[1]-1, so it should be >= 0. Additionally, that value uniquely defines the sequence, so we can create counter using a map to count which indexes create which values by the aforementioned rule. After that, we take the pair that has the maximum value (which must also be non-negative) — that is equivalent to the largest amount of indexes that match the same sequence. Getting the answer is the same as the editorial, it is n — x where x is the largest non-negative value in the map.