Let's discuss solutions! How to solve D, G and J?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 147 |
| 10 | TheScrasse | 146 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 19.02.2025 01:31:40 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Просто слив. =(((((
Что сдала команда Итмо в B за 5 минут?
Предпосчитаем количество делителей за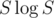 , а потом перебор в ней пишется за 2 минуты.
, а потом перебор в ней пишется за 2 минуты.
Как решать K?
И почему вот это решение падает: перебираем количество черных карт, которое мы могли вытянуть до того как вытянули последнюю красную, считаем вероятность вытянуть такое кол-во черных и кол-во способов их вытянуть вместе с красными, перемножаем, плюсуем к ответу.
Или иной вопрос: условие, что мы стараемся максимизировать выигрыш означает то, что мы не будем продолжать играть, когда красные карты закончатся, а не то, что мы будем продолжать играть, пока они есть?
Видимо речь о Div2
DP(n, m) = max(0, (1.0 + DP(n-1, m)) * n / (n + m) + (-1.0 + DP(n, m-1)) * m / (n + m))
J. Sort the edges. Binary search for the answer. Sliding window over the edges gives us a sequence of queries to add and remove edges; need to check if the graph ever becomes connected when executing the queries. This can be done using divide and conquer that uses DSU with rollbacks.
Could you please elaborate on "divide and conquer that uses DSU with rollbacks". I have never heard of this technique before, so could you please point me to some source or provide a short explanation. Thanks a lot.
Something like this: dynamic connectivity problem offline
"DSU with rollbacks" — it's partially persistent DSU. You can save all changes in stack and "rollback" to previous state when you want.
Yep, it's a part of Burunduk1's thesis.
Suppose we have a sequence of queries that add and remove edges, or get the number of connectivity components; for simplicity, each edge is added exactly once, then removed exactly once. The recursive procedure will take a segment of queries [a,b) and a global DSU that already contains all edges that are present in the graph for the whole segment [a,b) (i.e. edges that were added with queries [0,a) and removed with queries [b,n)). The procedure will answer all these queries and roll back all the changes that it makes to the DSU. To do that:
When we get to a segment [a,a+1), and query a asks for the number of connectivity components, we can just answer this query by looking at current state of the DSU.
(Actually I believe this can be implemented a little shorter if we pass the list of edges to the recursive procedure by value, but in this problem I was too paranoid about the TL to do that)
Thanks a lot. That is a very nice idea.
Just one clarification, in point 5 shouldn't it be removed with queries [b,n) instead of [c,n).
Fixed, thanks.
What is DSU with "rollback"?
G: Final order of numbers will be equivalent to sorting an array of pair(digit_sum(i), i). Now instead if you iterate through sum of digits, you can find number of numbers ≤ N and with given sum of digits using dp. For any given sum of digits at most one number can be in its correct place, which you can find by binary search.
Очень интересует решение F и B на div2?
F: Даже не знаю что может быть не ясно в этой задаче. Если 0 или 999999999 выводим -1. В противном случае можно либо вынести единичку, либо от чего-нибудь отнять единичку и к чему-нибудь прибавить. Не забыв убрать лидирующие нули если получаются.
B: Посчитаем сколько раз встречается каждое число во вводе. Переберём модуль, переберём числа имеющие остаток K по этому модулю, прибавим к ответу произведение количеств тех и других. Случай K=0 я отдельно рассматривал, там нужно учесть что i может быть равно j по условию.
Кто-то утолкал решение за O(M^2) в J?
Ага, с константой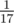 . Если было бы больше памяти, можно за
. Если было бы больше памяти, можно за 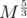 аналогично сделать.
аналогично сделать.
В чем основная идея ускорения, в двух словах? По коду просто тяжеловато понять :)
Разобьем наши ребра на K блоков, для всех подотрезков 0 ≤ i ≤ j < K этих блоков предпосчитаем СНМ, теперь на запрос является ли граф связным на отрезке мы можем отвечать за длину блока (идея аналогичная корневой декомпозиции). В итоге получаем, что время работы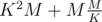 , что при
, что при  дает
дает 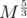
Можно ещё за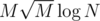 .
.
Двумя указателями по отсортированному списку рёбер ищем для каждого r такое максимальное l, что рёбра на отрезке [l, r] образуют одну компоненту. Для этого надо уметь добавлять и удалять рёбра из СНМ, но мы умеем удалять только последнее добавленное.
Тогда будем поддерживать такой инвариант: пусть сейчас рассматриваем отрезок [l, r] и p — минимальная точка в отрезке, такая, что она делится на K. Тогда в текущем СНМ-е у нас рёбра идут в порядке p, p + 1, ..., r. Теперь, чтобы пойти дальше, нужно уменьшить r (удалить последнее ребро) и пойти как можно дальше налево и обновить ответ. Теперь, если мы при этом пересекли контрольную точку левее p, то всё перестроим, иначе откатим изменения.
На яндексе заходит за 35 мс, code
Какая конструкция в H?
Вроде как, можно случайно накидать точек в треугольник и перебором найти подходящую триангуляцию.
Ну, у нас всё то же самое, только не перебор, а просто рандомно флипаем одно ребро (типа если есть рёбра ab, bc, ad, dc, ac, убираем ac и ставим bd). За несколько секунд находит ответ.
Что-то такое заходит. рисунок
strange, exactly this gives me wa1
0 0
1 2
1 3
1 4
1 5
2 1
2 2
2 3
2 4
3 1
3 2
3 3
4 1
4 2
5 1
10 0
0111110001001011
1010011000000000
1101001100000000
1010100110000000
1001000010000001
1100001001000000
0110010101100000
0011001010110000
0001100100010001
1000011000101000
0000001101011100
0000000110100101
1000000001100110
0000000000111011
1000000000001101
1000100010010110
D и E из второго дивизиона?
E вроде уже где-то видел, не могу вспомнить где.
Кто как решал E (про прямые)?
На всякий случай, я пытался делать так (wa3 :)):
1) прямые параллельны <=> их направляющие сонаправлены <=> их векторное произведение 0. Тогда беру
P = (A + C) / 2 (любая середина отрезка между точками на разных прямых), Q = P + (B — A)
2) нахожу пару ближайших точек (одна точка на первой прямой, вторая на второй), тогда
P = (E + F) / 2, Q = P + ((D — C) + (B — A)) (потому что сумма векторов будет биссектрисой угла между ними)
Угол всегда 180 :)
Все правильно, но во втором случае D-C и B-A нормализовать надо.
Спасибо! У меня стоит assert, что на координаты меньше 2000, пока что он не падал.
Что ж, буду искать баг.
UPD: кажется понял, о чём вы говорите, нужно нормализовать 2 направляющие независимо
Сдал наконец, главная проблема была в том, что ближайшие точки я искал тернарником и это не проходило по точности.
Когда подумал и написал 5 строчек формулой, то сразу зашло.
UPD: на самом деле проблема была в том, что у меня значение в тернарнике сравнивались с EPS
where can i see the problems??
http://opencup.ru/files/ocf/gp14/problems2-e.pdf
It will be here — Ural Championship 2015
Here is a solution of problem D.
If k = 2^x, the answer is always yes (Obviously). Else if k = 2x-1 or k = 2x, then f(k), the minimal n for which the answer is yes, equals to 2x+1.
f(2*x-1) >= 2x+1. |> Lets consider the last step, on which number k was obtained. (a, b) -> (a-b, 2b). 2b can't be equal to 2x-1. Then a-b = 2x-1; a >= 2x; b >= 1; n >= a+b >= 2x+1 <|
f(2*x) >= 2x+1, x is not a power of 2. |> Let p be an odd prime divisor of x. Initially all numbers equal to 1, thus are not divisible by p. The following invariant takes place: there is always a number which is not divisible by p. Indeed, if (a, b) -> (a-b, 2b) and a-b and 2b are divisible by p, then a and b are divisible by p. That means, we can not obtain a situation where one number is equal to 2x, and all other numbers equal to 0. Therefore n >= 2x+1 <|
Now if n = 2x+1, how to obtain 2x and 2x-1? The trick is to divide all the substance in two parts of volumes a and b, one of which is a power of 2. Then repeat the action on the two tubes until we are done. Why this works? Let's concider an action (a, b) -> (a-b, 2b). Since a+b = n, (a-b, 2b) = (2a%n, 2b%n). Therefore after t steps (a, b) will turn into (2^t*a%n, 2^t*b%n). Since n is odd and one of (a, b) is a power of 2, after some steps, this number will turn into 1, and on the next step it will turn into 2. Then the other number will be n-1 and n-2.
The only thing left is to divide in two parts. Let 2^x be the biggest power of 2 which does not exceed n. First unite 2^x tubes into one. Then after y steps you have (n-2^x)/(2^y) rounded up pieces of volume 2^y and one piece containing all the remaining volume. On y-th step you divide pieces of volume 2^(y-1) into pairs and unite them. If one piece was left without pair, you append it with the remaining piece. After x steps you have one piece of volume 2^y and one more piece containing all the remaining substance.