Добрый день.
Это пост о мелочах в реализации хешей.
Сегодня ребята гуглили "как писать полиномиальные хеши", но нагулили лишь две ссылки на тему "как не надо писать полиномиальные хеши" — e-maxx и habr.
А можно писать иначе — short и full. Последняя версия устойчива к антихеш тестам, её можно копипастить.
Теперь подробно. Есть два способа. Оба для краткости будут написаны по модулю 264, то есть падают на строке Туе-Морса.
Общая часть:
const int P = 239017; // Если брать простой модуль, здесь стоит писать rand()!
// s - строка, n - её длина
Первый способ (я пишу так):
// deg[] = {1, P, P^2, P^3, ...}
// h[] = {0, s[0], s[0]*P + s[1], s[0]*P^2 + s[1]*P + s[2], ...}
unsigned long long h[n + 1], deg[n + 1];
h[0] = 0, deg[0] = 1;
for (int i = 0; i < n; i++) {
h[i + 1] = h[i] * P + s[i];
deg[i + 1] = deg[i] * P;
}
auto get_hash = [&]( int l, int r ) { // [l..r]
return h[r + 1] - h[l] * deg[r - l + 1];
};
Второй способ:
// deg[] = {1, P, P^2, P^3, ...}
// h[] = {s[0], s[0] + s[1]*P, s[0] + s[1]*P + s[2]*P^2, ...}
unsigned long long h[n], deg[n];
h[0] = s[0], deg[0] = 1;
for (int i = 1; i < n; i++) {
deg[i] = deg[i - 1] * P;
h[i] = h[i - 1] + s[i] * deg[i];
}
auto get_hash = [&]( int l, int r ) { // [l..r]
if (l == 0)
return h[r];
return h[r] - h[l - 1];
};
Отличия здесь два
Направление s0Pn - 1 + s1Pn - 2 + ... + sn - 1 или s0 + s1P + s2P2 + ... + sn - 1Pn - 1?
В первом способе, чтобы сравнить две строки [l1..r1] и [l2..r2], достаточно написать get_hash(l1, r1) == get_hash(l2, r2). То есть, функция get_hash честно возвращает хеш. Можно, например, найти количество различных подстрок, положив все хеши в хеш-таблицу.
Во втором случае функция get_hash на самом деле возвращает не хеш, а хеш, домноженный на некоторую степень P, поэтому придётся писать так deg[r2] * get_hash(l1, r1) == deg[r1] * get_hash(l2, r2) (на e-maxx правда чуть страшнее). А использовать хеши иначе не получится. Можно модифицировать функцию get_hash, использовать честный хеш true_hash(l, r) = deg[n - r - 1] * get_hash(l, r), но у такого способа есть минус — мы предполагаем, что знаем максимальную длину строки. Это не всегда удобно, а при онлайн-решениях иногда и не правда.
У второго способа ещё есть вариация с делением по модулю. Так писать точно не нужно.
С чего начинать массив h? С 0 или с s[0]?
Если мы начинаем с 0, мы получаем более короткий и быстрый код (да, да, чтобы if-у выполниться, нужно время!). Оценивая скорость, заметьте, что умножений будет столько же.
Если же мы начинаем в s[0], то получаем массив длины n, то есть экономим O(1) памяти.
Как лучше, решайте сами. Я всем рекламирую первый вариант. Если есть конструктивные замечания или альтернативные версии, буду рад услышать.
Выбор простого модуля
Отдельный привет всем, кто говорит "число P можно выбирать любым". P должно быть больше размера алфавита. Если это так, то хеш, вычисленный без взятия по модулю, как длинное число, инъективен. Иначе уже на этапе вычисления без модуля могут быть коллизии. Примеры, как нельзя делать: алфавит "a..z", P = 13, алфавит ASCII 33..127, P = 31.
P.S. Кстати, как правильно пишется "хеш", или "хэш"? Моя версия — "хеш".
UPD: Подсказывают, что, если писать без unsigned, получится Undefined Behaviour. Спасибо Лёше Левину.
UPD: Чтобы хеш точно нельзя было сломать, можно точку P выбирать как max(Σ, rand()). Версия full пропатчилась. Спасибо Kaban-5, nk.karpov.











Скажите, а почему нельзя писать хеши как на e-maxx?
Их умеет взламывать не только chuck
А причём тут chuck?
А при том, что при виде Чака любое решение в страхе ломается.
А где же эталонный вариант, как писать надо, чтоб хэши не падали, в том числе и на строке Туэ-Морса?
В ссылке на full они не падают)
Сейчас еще модно делать защиту от взломов на CF: 2 модуля выбирать не 109 + 7 и 109 + 9, а два рандомных больших простых числа)
Скажите, а почему именно 2 модуля?
Ну нужно >=2 чтобы не случилось просто коллизии случайно. Можно брать и больше, просто тогда программа будет работать дольше)
Спасибо.
А как бы их покороче ещё сгенерить эти два случайных простых числа...
Ну мы обычно делали так: шли циклом от 10^9 и проверяли чила на простоту за корень. Как только сгенили приличное число простых(~10), выбираем из них 2 рандомных различных.
Почему бы просто не тыкать в случайные большие числа и проверять на простоту? Кажется, это должно не сильно долго работать. А то может найтись маньяк, который заранее нагенерит 45 котрпримеров для всех пар 10 простых(Интересная идея! Надо будет попробовать поманьячить).
Как маньяк узнает, какую под какую пару пускать тест в ход, если пара случайно выбирается?
Ну если задача специфичная, то он может эти примеры склеить друг с другом
Можно просто выбрать случайное число и от него искать следующее простое
Так может зашить штук 10, а потом случайно 2 из них выбрать?
Для этого их нужно заранее подготовить)
http://compoasso.free.fr/primelistweb/page/prime/liste_online_en.php Вот тут можно взять
Как будто эти два не рандомные)
Слишком популярные.
Казалось бы, зачем случайный модуль, если я могу взять случайную точку.
Хм, да, так вроде проще. Круто)
Казалось бы зачем два простых модуля, когда можно взять один 10e18 + 3 :)
По нему перемножать дольше? Я умею только через long double, который не везде есть.
В gcc есть __int128. Правда, я только слышал о нём, но ни разу не пользовался.
Он есть ещё в меньшем числе мест.
а где вообще есть? я уже не первый раз вижу, но никогда не удовалась скомпилировать такой код. Нужны какие-то спе библиотеки??
Нужна 64-битная версия gcc. Например, под Windows это может быть tdm-gcc-64.
А зачем брать точку простой? Нужно лишь брать точку с большим порядком по модулю основания хэша, в идеале первообразный корень (конечно, больший размера алфавита). Эти вещи, как я понимаю, слабо коррелируют.
Вы меня простите, но точку надо брать случайной (написать в коде rand()), тогда всё будет нормально работать. Иначе любому хэшу, можно легко подобрать коллизию. Я умею строить например для модулей порядка 1e36 не слишком большой тест из двух букв, за разумное время.
А можешь подробнее рассказать, как его строить?
Коля скорее всего имеет в виду метод Капуна
Хм, но вроде бы, если я буду использовать случайный модуль, то таким методом коллизию найти не получится. Т. е. видимо смысл в том, что хотя бы один из параметров хеша должен быть случайным.
Насколько я понял, Коля говорит так
Если и точка, и модуль детерминированы, то легко ломать (по ссылке алгоритм)
Значит, нужны или случайная точка, или случайный модуль. Случайную точку брать проще, так как она не обязана быть простой.
UPD: (s0 + s1 * P) % M. Здесь M — модуль, а P — точка, которую мы подставляем в многочлен.
Понятно. Просто мне, как человеку, который пишет на джаве, можно воспользоваться функцией nextProbablePrime у BigInteger, поэтому я в последнее время делаю модуль случайным простым, а точку константой.
В первом приближении да, но когда элементов становится мало (<40) можно в лоб перебирать все подмножества. Это заметно уменьшает размер теста.
А можно этот метод чуточку поподробнее описать?
Задача с чемпионата СПБГУ
Моё решение
Спасибо!
А есть какое-нибудь объяснение, почему это работает и с какой асимптотикой?
Мы хотим сгенерить 2 строки длины n над алфавитом {a, b}, у котороых (P, M) хеш одинаковый. Hash(s0s1...sn - 1) == Hash(t0t1...tn - 1) ⇔ ΣiPicoefi = 0 (mod M). Здесь coefi ∈ {-1, 0, +1}.
Осталось найти такие коэффициенты.
Возьмём a0 = {P0 mod M, P1 mod M, ... Pn - 1 mod M}.
Мы верим, что a0 содержит n случайных равномерно распределённых чисел от 0 до M.
Теперь из ai получим ai + 1.
Диапазон чисел в ai обозначим за Mi (M0 = M).
Длина ai + 1 в два раза меньше, чем длина ai.
Поскольку b[i+1] — b[i] ≈ Mi/n, то диапазон массива ai + 1 примерно в n раз меньше диапазона массива ai.
Мы верим, что если числа в ai распределены равномерно, то и числа в ai + 1 распределены примерно равномерно.
Алгоритм завершается, как только b[0] = 0.
Оцени n при котором диапазон успеет сойтись от M к единице: n(n/2)(n/4)(n/8)... ≥ M ⇔ nlogn / 21 + 2 + ... + logn ≥ M ⇔ 2log2n - logn(logn + 1) / 2 ≥ M ⇔ 2log2n / 2 ≥ M ⇔ logn ≥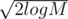 ⇔ n ≥
⇔ n ≥ 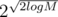 .
.
Подставляем M = 1018, получаем n ≥ 2048.
Круто, спасибо!
Позволь позанудничать. В своей оценке ты дважды делаешь преобразования не тождественные, а приводящие к более сильным неравенствам, поэтому знак должен быть не ⇔, а ⇐ или ∵. Тождественно вот так (по-прежнему предполагая, что n есть степень двойки):
Правда, после округления до степени двойки для M = 1018 всё равно получается n ≥ 2048.
А логарифм в ТеХе пишется так:
\log.…А вообще за объяснение спасибо!
Спасибо за строгую версию рассуждений =)
Мне не нравится вёрстка tex-а на CF, без нужды стараюсь tex-ом здесь не пользоваться.
У меня есть конструктивное замечание: зачем вообще упомянут второй способ, если он во всех отношениях хуже?
Валер, а ты переходил по ссылкам на хабр и емакс? Только поэтому. Потому что многие так пишут.
Да, переходил, конечно. То есть, чтобы показать, чем этот вариант плох? Окей.
Вот так лучше вообще не делать, так как без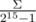 под Windows, где Σ — размер алфавита, то есть почти гарантированно упадёт на каком-нибудь тесте.
под Windows, где Σ — размер алфавита, то есть почти гарантированно упадёт на каком-нибудь тесте.
srand()это бесполезно, иначе работает неправильно с вероятностьюКстати, если уж так хочется избежать взлома, то инициализроваться надо не от
time(), а от чего-то, что может принимать очень много разных значений за короткий промежуток времени, так как взломщик-маньяк может склеить контрпримеры для всех значенийtime()на минуту вперёд.P. S. Первое замечание уже поправили, но как-то не очень надёжно выглядит...
P. P. S. "почти гарантированно упадёт на каком-нибудь тесте" — неправда, туплю, вероятность значима только есть тестов 2000 или больше.
Насколько я понимаю, если модуль простой, P можно брать любым больше Σ. Почему нет? У меня в коде стоит max(239, rand()). В посте сейчас тоже поправлю.
Когда я начинал писать комментарий, было просто
rand(). Второй пункт всё равно в силе, да иmax(239, rand())очень часто бывает равным 239.UPD: Ок, я идиот, нужно тестов 200 конкретно против точки 239, чтобы это упало с хорошей вероятностью.
Ну ооочень часто :D
В нормальных системах rand() возвращает число из [0, 231 - 1], если писать хэши по двум модулям и брать основания независимо, то вероятность события которое описанно < 10 - 15. Но если быть совсем честным, можно использовать то, что лежит в random, говорят там генераторы случайных чисел написанны хорошо.
Если есть С++11, то можно делать так:
srand(chrono::duration_cast<chrono::nanoseconds>(chrono::high_resolution_clock::now() - chrono::high_resolution_clock::time_point()).count()).И под MSVC
__rdtsc()— это не часть стандарта, на разных компиляторах она в разных библиотеках лежит и никто не гарантирует ее наличия.хотел написать, что в C++11 есть
std::random_device, но выяснилось, что в MinGW этот класс всегда возвращает одни и те же числа.Кстати,
high_resolution_clockв MinGW тоже не совсем "high resolution": возвращает время с точностью только до микросекунд, а не до нано.Ничего себе! Интересно, в libstdc++ примут патчи, исправляющие это безобразие добавлением специального кода для Windows?
FWIW, код
std::random_deviceиз libc++ подсказывает, что на Windows можно использовать функциюrand_s.Чуть короче:
Есть небольшое общее замечание, пока у меня не получается сделать из него что-либо конкретное. Речь идет об оценке вероятности ошибки сравнения строк для реализации, в которой рандомизируется MUL и фиксируется MOD в полиномиальном хеше.
Для начала, несколько общих моментов. Пусть P(x) — многочлен степени n по модулю p (разницу hash(s1) — hash(s2) можно рассматривать как такой многочлен).
Несколько утверждений:
1. Вероятность того, что заданный x является корнем случайного многочлена P равна 1/p (является корнем при ровно одном свободном члене).
2. Среднее количество различных корней многочлена P равно 1 (предыдущее утверждение суммируется по всем x).
3. В худшем случае число корней многочлена P равно n.
Таким образом, для полиномиального хеша при случайном MUL для случайных различных строк s1 и s2 вероятность равенства hash(s1)=hash(s2) равна 1/MOD, а в худшем случае относительно s1 и s2 данная вероятность равна max(|s1|,|s2|)/MOD. В общем, худший случай существенно отличается от среднего.
Если получится построить пример для приложенного кода lcp такой, что все сравнения будут проходить по худшему случаю, вероятность провала каждого запроса lcp будет иметь порядок |s|^2/(p1*p2).
К сожалению, построение многочлена, имеющего много корней в ограничениях на коэффициенты многочлена наталкивается (на моем уровне знаний алгебры) на технические сложности. Если я правильно считаю оценки, вероятность того, что при k << p случайный многочлен имеет k различных корней равна (1/k!), т.е. случайная генерация не приводит к результату. Единственное известное мне достаточно быстрое построение многочлена в ограничениях на коэффициенты, имеющего один заданный корень (тот-самый-алгоритм-с-разностями), дает степень порядка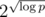 , что существенно выше степени минимального такого многочлена и, похоже, неприменимо для задачи. В общем, нужны дальнейшие исследования.
, что существенно выше степени минимального такого многочлена и, похоже, неприменимо для задачи. В общем, нужны дальнейшие исследования.
На всякий случай хочу проверить: правильно ли я понимаю, что при простых модулях точку можно брать любую, большую размера алфавита (или большую или равную?) и меньшую каждого модуля? И что 239 в твоём коде — это просто красивое число, большее любого встречаемого в задачах алфавита, но его спокойно можно заменить на, например, 256 или real_alphabet_size+1?
Да, всё так.
P.S. С вероятностью правда непонятки. I_love_natalia разбирался, но вопросы остались.
А почему " если писать без unsigned, получится Undefined Behaviour " ?
Потому что переполнение знаковых типов (например,
intилиlong long) — undefined behavior по стандарту языка.Можете привести небольшой пример на коллизию
P=3, hash(da) = 3 + 0*3 = 3, hash(ab) = 0 + 1*3 = 3
P = 264 подстроки Туе-Морса
Здравствуйте! Хотелось бы узнать правильно ли я рассуждаю: при нахождении хеша подстроки в том варианте, котором используете вы, там вычитание двух хешей return h[r + 1] — h[l] * deg[r — l + 1] после данной операции ответ будет по модулю 2^64, получим ли мы при этом правильный ответ? Дело в том что на некоторых сайтах предлагается к ответу прибавить base: h = ((hash[r] — hash[l — 1] * pow[r — l + 1]) % base + base) % base, обязательно ли это?
если делать в unsigned long long, как написано здесь, это необязательно. если же модуль будет другой, то так делать нужно
А может кто-нибудь сюда скинуть коды невзламываемых реализаций хэша с acm.math.spbu? А то не открывается почему-то сайт
upd. заработал
А где можно найти объяснение работоспособности формулы, используемой в первом способе?
h[r + 1] - h[l] * deg[r - l + 1];Можно выписать, что за многочлены хранятся в этих двух позициях в массиве
h, а потом вычесть один из другого.