В задаче нужно написать то, что просят по условию: пока в номере года есть совпадающие цифры, прибавляем к номеру 1.
Предпосчитаем для каждого числа от 1 до 105 следующее простое. Это можно сделать абсолютно любым способом. Главное — не забыть при проверке числа на простоту перебирать делители до корня из числа.
Теперь для каждого элемента матрицы легко понять, сколько к нему нужно прибавить, чтобы получить простое число. После этого остается просто найти строку или столбец с наименьшей суммой.
Если 3k > n, решения нет (потому что каждое множество должно содержать хотя бы 3 элемента). Иначе подходит, например, любое разбиение, в котором первые 3k чисел розданы следующим образом:
1 1 2 2 3 3 ... k k 1 2 3 ... k
Для каждого из k множеств, разность между вторым и первым элементами будет 1. При этом ясно, что разность между третьим и вторым элементами будет не 1 (более точно: 2k - i - 1 для i-го множества). Поэтому каждое множество точно не образует арифметическую прогрессию.
При этом не важно, как раздавать оставшиеся n - 3k чисел.
Построим из всех суффиксов строки бор (он же — несжатое суффиксное дерево). Давайте перебирать подстроки в порядке возрастания индексов, то есть сначала [1...1], затем [1...2], [1...3], ..., [1...n], [2...2], [2...3], ..., [2...n], ... Заметим, что переход от одной строки к следующей по сути означает добавление одного символа в конец. Поэтому несложно поддерживать количество плохих букв и "текущую" вершину в боре. Если количество плохих букв не превосходит k, то строка — хорошая. И соответствующую вершину в боре нужно пометить, если она не была помечена ранее. Итоговый ответ — количество помеченных вершин в боре.
Есть также более простое решение, в котором вместо бора используются полиномиальные хэши для поиска количества различных по содержанию подстрок. Нужно просто посчитать хэши для всех хороших подстрок, отсортировать, и посчитать количество различных хэшей (одинаковые хэши после сортировки окажутся на соседних позициях). Однако, решения с такими хэшами крайне ненадежны, и всегда лучше писать точное решение.
Утверждается, что любую пару вида (x, y) (x < y) можно привести к виду (1, 1 + k·d), где d — максимальный нечетный делитель числа y - x, а k — любое положительное целое число. Значит, каждое из (ai - 1) должно делится на d, то есть d является делителем gcd(a1 - 1, ..., an - 1), и его можно перебрать. Давайте посмотрим, для каких исходных пар d является максимальным нечетным делителем разности — это все пары с разностью ровно d, 2d, 4d, 8d, 16d и так далее. Вспомним, что числа в исходной паре не должны превышать m, а значит количество пар с фиксированной разностью t — ровно m - t.
Итоговое решение: просуммировать (m - 2ld) по всем d — нечетным делителям gcd(a1 - 1, ..., an - 1), при условии, что 2ld ≤ m.
Быстро однако :)
Комментарий заплюсовали больше, чем пост
Слава богу в 4 и хеши прошли
А что за решение с хэшами?
Переберем все хорошие подстроки, кол-во различных подстрок получим при помощи хэшей, это кол-во различных значений хэшей этих подстрок.
А какой тип хеш-функции удобно использовать при работе с длинными строками?
Удобно использовать полиномиальные хэши по простому модулю.
Не oбязательно по простому модулю, главное не по 2^64.
Немножко непонятно... Можно для Див2 разборы писать поразборчевее? С примерами что-ли.. Хотя бы так. Мы ведь для того читаем разборы, чтоб чему нибудь новому научится :)
Что именно непонятно?
C) Почему такое решение правильно? D) Ничего непонятно. Нету решения попроще?
Кое-что дописал.
По поводу хэшей зря так пренебрежительно. Мы всегда писали хэши по паре простых модулей, и еще ни разу не попадались коллизии. И писать в разы проще.
А если I_love_natalia взломает?
Ну чтож как говорится удачного взлома.
Кстати говоря есть же какой нибудь стандартный подход поиска строк (поправка с теорией, и например приемлемой длины) с одинаковыми хэшами , может кто ссылкой на литературу поделиться
Есть такая вещь, которая в народе ходит с названием "Метод Капуна(eatmore)".
Вкратце. Будем генерировать две строки из букв a,b. Причем так, что bb не бывает, в одной паре символов. Тогда фактически бывает ( + 1, - 1, 0) * pk к разности хешей. Надо набрать нетривиальный 0.
Будем делать так. Отсортируем, возьмем разности двух соседних. Отсортируем, возьмем разности двух соседних...
Вроде хорошо работает (эксперементально) для хеша с любыми известными параметрами.
Это решает проблему, с большими основаниями для хеша. Проблему, с много модулей можно решать как описано у I_love_natalia.
Только в определенный момент, если нет написанного кода, писать такой генератор станет не выгодно, но теоретически, чтобы быть уверенным, надо брать случайным другой параметр.
Я думаю , если добавить еще одну хеш-функцию , то не взламает , а если взламает , то можно сделать и третью )))
Если не рандомизируешь хеши — обязательно взламаю три хеш-функции. Там написано, как.
Прошел по ссылке , печаль =( Но мы сделаемь вторую и третью функции до 10^18 и все пройдет ... надеюсь )
А по модулю 10^18 множить сложно без 128-битных чисел.
кстати, Вы не могли бы поподробнее описать как это можно эффективно сделать, без 128-битных чисел?
Умножать два 64-битных числа по модулю можно за log(min(a, b)) так же как и возводить в степень. Т.е. a*b = 2*(a/2)*b(если a нечетное) и b+(a-1)*b если a нечетное
Ну... в первый раз было сложно, потом как-то привыкли :-)
Умножение за O(1): mul(a,b,m)
А как нормально объяснить, что это работает правильно? Казалось бы, всё зависит только от масштабов погрешности при вычислении (a * b) / m, почему она не будет настолько большой, что a * b — r * m повторно переполнится?
До 263 можно вообще написать так (один if вместо двух while):
Доказать можно, например, так. Заметим, что умножение и последующее деление в long double правильно вычисляют как минимум 63 знака результата, то есть значение выражения
(long double) a * b / cотличается от точного не больше, чем на c / 263 < 1. Между тем, если бы погрешность ответа была больше c или вообще больше пределов int64_t, то погрешность temp была бы больше единицы.А для чисел, больших 263, даже с модулем надо очень аккуратно писать.
Гасса, по-моему, ты не совсем прав.
Берем mingw g++ 4.7.3
Пускаем стресс твоего кода для
assert падает.
И правда не работает. Прошу прощения.
По тому, что настрессилось, похоже, что баг в утверждении
умножение и последующее деление в long doubleправильно вычисляют как минимум 63 знака результата— правильных знаков всего 62?!Для M = 262 - ε стресс-тест не падает. Ну и на том спасибо.
Больше того, если (1LL << 62) * 1.41, у меня уже не падает :-)
Ну да, а с 1.42 падает раз в четыре с небольшим миллиона тестов.
В общем, хорошо, что я в авторских решениях перестраховывался и писал за логарифм :) .
А чем плохо такое решение с хэшами? Работает достаточно быстро. http://codeforces.me/contest/271/submission/3107201 Тут просто сохраняются границы подстроки в хэш-таблицу, и при совпадении хэша стоки полностью сравниваются.
Возможно многие посчитают мой вопрос не в тему, но всё же:
Как можно сжать бор , чтоб поменьше памяти использовал? Задача у меня такая , дана строка , длина , которой в худшем 4000. Надо сделать бор из каждого суффикса. Простой бор будет использовать много памяти. Скажите, если знаете как можно сжать бор. Спасибо.
Можно хранить все переходы в большой хеш таблице.
А можно чуть подробнее? я храню переходы для каждой вершины в структуре, как описывается в emaxx. По этой причине не могу сдатьантимат, получаю ML :(
Is there any background in problem E?
In 4rth q after so many TLE's I have drawn an inference that generally map is slower than set though both being dynamic memory allocation....
I'm quiet new in Java,I keep getting TLE and use trie data structure,any advises?(Though the same code written in C++ got AC) code
It's not because you use Java, it's because you make a lot of substring() calls.
Thanks,so is there a faster way to remove the first character from string?Or i should use array of chars instead of strings or something like that
Just remember where the string really begins.
Yup thanks got it
А в Е почему нельзя получить (1,1+k*d+i)? Получили, например (1,1+k*d), i раз показали серому коню, получили (1+i,1+k*d+i), показали (1,1+k*d) и (1+i,1+k*d+i) серо-белому и получили (1,1+k*d+i). Где я ошибся?
1+k*d != 1+i, а по условию серо-белому можно показывать только пары вида (a,b) и (b,c)
спасибо
Серо-белому мы показываем (a,b) (b, c), т.е. в вашем случае i = k*d
Слегка оффтоп. Подскажите, пожалуйста, в чем проблема этого кода 3109675? Я явно не знаю чего-то важного про свой язык. Примерно догадываюсь, ибо вот так 3109702 зашло, но точно не знаю.
Как надо писать. Используй PrintWriter, а System.out.*, насколько я понимаю, после каждого вывода flush'ет все написанное, и соответственно работает долго. Ну и общее для всех языков — выводить по одному символу/числу всегда долго (т. е. порядка 10^5 скорее всего еще нормально, а 10^6 лучше не рисковать, хотя данная задача у меня на Java работает <500 мс и выводит все числа отдельно).
Обычно и использую PrintWriter, в этот раз что-то перемкнуло. Тем не менее, не знал, что Syso так сильно тормозит и почему, спасибо.
i m not getting the problem E' editorial can any one explain ?
Here is the proof for the solution given in the editorial.
Может ли кто нибудь объяснить почему "Утверждается, что любую пару вида (x, y) (x < y) можно привести к виду (1, 1 + k·d), где d — максимальный нечетный делитель числа y - x, а k — любое положительное целое число." ?
Пусть есть пара (a, a + d), где d — четное, мы ее можем привести к виду (2a, 2a + d), потом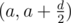
Теперь d нечетное. Получим из пары (a, a + d) пару (a + d, a + 2d). Из этих пар получим (a, a + 2d), если a нечетное, возьмем пару (a + 1, a + 1 + 2d), поделив получим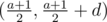
. Будем повторять операцию пока не получим (1, 1 + d).
Из пары (1, 1 + d) можно получить (1 + d, 1 + 2d), из них (1, 1 + 2d) потом (1 + d, 1 + 3d) -> (1, 1 + 3d) ...
Спасибо )
Я тупой )
Попробуй перебрать все числа x подряд до корня из d. Делителем будет либо x либо
, других делителей нет.
For problem 4, suffix array with lcp can also be used. We can first pre-compute the bad character count for all the substrings and store it in a table. Then, iterating through the suffix array and avoiding duplicate substrings using the lcp table, we can find the answer.
Hello. I am having trouble with the problem D (getting TLE). I am using the trie to solve the problem. When I build it, I already keep track of the current number of bad characters. If it is bigger than k, I leave the recursion. The final answer is the number of nodes of the tree.
Could anyone help me please? What am I doing wrong? Code
Why do you have these 2 nested loops in main() function? You are not really using
ianywhere.OMG, thanks RAD. It was something I was trying and forgot to remove.
Problem C: in each set Ui, its elements ui, 1, ui, 2, ..., ui, |Ui| do not form an arithmetic progression (in particular, |Ui| ≥ 3 should hold). What's the meaning of it ? Does it means when Ui < 3 there is no necessary to hold this condition ?
Can you tell me what's wrong of my code ? Problem D: 3145554
Complexity
I don't think so, I learned from this AC submission? Why his is ok ? 3105181
Try to find out what is the complexity of string comparisons
so you're saying that insertion in set is taking time??
You can implement it using sets but I think you have to iterate for len =1 to len=n and index 0 to n-len; after every len you have to clear your set to prevent it from exceeding memory limit
В условии задачи "271B — Простая матрица" написано: "Все числа в исходной матрице не превосходят 10^5" На 16м тесте получил WRONG_ANSWER с тестсетом: Ввод 500 500 12049 94371 7867 74623 18885 10113 26774 47637 76701 73692 74195 4160 94333 37410 66541 1199 27239 52785 71905 47842 62308 10971 8560 63210 97819 50498 12505 42028 70200 28028 44579 62078 34406 89615 57617 98120 27861 12181 85291 45956 95828 85881 81979 7839 59479 27960 16236 90485 33265 46465 76333 62455 13691 245 38380 80872 39147 39046 5339 66203 20829 48219 58478 1047 31885 714 96603 71507 97242 58909 4664 76505 88837 51661 72415 35942 5871 96425 80236 18184 67358 80272 65725 36254 30072 50642...
Это ошибка в условии? Или "не превосходят 10^5" означает, что порядок = 5?
Видимо, не превосходят 105 значит, что любое aij ≤ 100000.
Problem D 271D - Good Substrings : This is my code. I've used the concept of Rolling hash/Rabin Karp algorithm. But I guess there are some collisions happening and it's failing on test case number 8. Any help is greatly appreciated. Been trying this for a long time.
Code: 27820412
Update: Solved! I tried many different ways. Initially, I used two hash moduli instead of one, but this exceeded the Time Limit on test #8 (Which is weird!). I ended up using a really large prime (About the size of 2^50) which just passed the time limit for Testcase #8 and passed the cases as well. :)
ya i was also getting wrong answer due to collisions so just used two different numbers 31 and 67 with modulo 1e9+7 and it got accepted
D can be solved using 2 pointer and little bit of a lcp array.This is my solution. https://codeforces.me/contest/271/submission/44768791
Не могу понять, почему в D во втором тесте ответ 8, там ведь все подстроки будут хорошими
Всё, понял, не надо минусов pls
бан на**й
ето смэрть
Problem C is like using 2 hashes of 10^9 size-TLE Using 1hash of 10^9 size -WA and using a very big hash and multiplying recursive -TLE
Problem D is like using 2 hashes of 10^9 size-TLE Using 1hash of 10^9 size -WA and using a very big hash and multiplying recursive -TLE
Beautiful Year https://github.com/arsalanhub/CodeForces/blob/master/Beautiful%20Year
Hey. Please stop spamming on every tutorial blog with your solutions of Div2 A problems. There are already many solutions available in the submissions section. You're not helping anyone at all. You're just spamming and also unnecessarily bringing old posts in the Recent Actions section.
271D using Z algorithm: https://codeforces.me/contest/271/submission/68098565
prereq: distinct substring using Z ( read it from CP algo ).
Implementation: Now I am assuming you know distinct substr using Z, then: we start counting the answer for a prefix after the zmax of that prefix. ( because we'll have distinct substring only after zmax)
can enyone help me with D problem? I am tring to sove it with hash but it has wrong answer on testcase 8;
https://codeforces.me/contest/271/submission/243292259
Yeah, you will get WA because there are more than 1e6 sub-strings that you will compare using hashes, which gives a very high chance of collision. So you should use two hashes instead of a single one, I used two by just changing the modulo.
Here is my AC submission : https://codeforces.me/contest/271/submission/245638497
thanks
try submitting the same solution again, it will TLE in tc8
Yes you are right. I tried with some optimizations like using arrays instead of vectors and bit operations inside Exponentiation and it passes but barely
In D, in sample test case 1 explanation, bab is given as a good substring but not aba. As b is a bad letter, bab should be a bad substring and aba should be a good substring. In sample test case 2 also, the solution is limiting only to two characters but there is no such constraint in the problem statement. please help me understand the question.
If you will read the question carefully, it is given that If the i-th character of this string equals "1", then the i-th English letter is good, otherwise it's bad. In the first testcase, the value of k is 1 , i.e., we can have at most 1 bad letter, in this case which is 'a'. So, "aba" is a bad substring because it contains two 'a', whereas "bab" is a good as it contains only 1 'a'.
i have facing problem with D (good substring) i am facing time limit exceed but i have implemented trie and still it is slow here is my solution 272082061 any help is appreciated
thank you!!