...состоится 16 апреля в 20:00 МСК
→ Обратите внимание
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 8 | luogu_official | 150 |
| 10 | awoo | 148 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 07.03.2025 05:40:54 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Удобное время проведения матча - похоже, что сегодня будет лимит регистраций.
За 40 минут до конца - уже 1733.
В качестве альтернативы для того чтобы посчитать, какова вероятность того, что очередную деревню мы добавим раньше данной при том, что все предыдущее деревни добавим после, можно было организовать ДП в котором мы почитаем сколько способов перестановок удовлетворяющих условию выше существует.
У меня были параметры DP(pos, flag_a, flag_b, bad_villages, usual_villages). pos -- текущая позиция в перестановке, flag_a - поставлена ли очередная деревня, flag_b -- поставленна ли данная (обрабатываемая) деревня, bad_villages -- сколько деревень должно быть еще поставлено из тех, которые должны стоять строго дальше обрабатываемой, usual_vilages -- кол-во деревень которые надо поставить и которые ни как не влияют на рассчет вероятности.
Естественно порядок надо соблюдать порядок расстановки ))
Для каждой деревни посчитаем матожидание расстояния дороги, идущей из нее. Ясно, что идти она будет в ближайший к ней город или в деревню, которые еще ближе этого города. Найдем все такие деревни, пусть их n - 1(с нашей n), занумеруем их от 1 до n в порядке увеличения расстояния (n будет значить, что дорога пойдет в город).
Теперь надо посчитать вероятность, что дорога пойдет именно в какую-то из них. Если она пойдет в k-ую из них, то посмотрим в каком порядке первые k деревень плюс n-ая будут соединяться. Всего вариантов (k + 1)!, хороших из них (k - 1)!(когда идет сначала k-ая, потом наша, потом остальные в любом порядке), т. е. соответствующая вероятность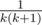
Вероятность того, что дорога пойдет в город очевидно равна 1 / k
Кстати получилось еще одно доказательство того, что
Да уж, в очередной раз понял, что меня от топа отделяют еще годы тренировок.
Сегодняшнюю 250 я уже видел, так что я точно знал правильное решение... Тем не менее, пока я дочитал условие и понял, что это именно то, что я уже когда-то решал, а после этого описал класс и метод решения, некоторые (Egor, к примеру) уже задачу сдали.
А пока я еще и написал решение, перечитал его раз и проверил на примерах и сдал, то оказался по времени на этой задаче только 27ым...
Тем не менее, "я еще только учусь", так что не все так плохо; а автору + за задачу:)
Пойду разбираться с решением 500, на контесте у меня на нее получились только комбинаторика настолько неудобная, что я в ней запутался, и очевидное решение за 2^N.