What should be the approach to find all paths with maximum flow? The graph is directed acyclic graph and the maximum number of nodes(vertices) in the graph can be 40 and edges around 80. Also, most of the edges have unit capacity.
→ Pay attention
Before contest
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:16:39
Register now »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
11:16:39
Register now »
*has extra registration
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/23/2024 06:18:22 (l1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Flow isn't fixed on a single path, that's quite trivial... but okay: maxflow along a path is just the minimum of capacities of its edges, so you want to find the maximum capacity c such that there's at least one path from the source to the sink (binseach+BFS) using only edges with capacity ≥ c, then only take edges with capacity ≥ c and find the number of paths — for DAGs, it can be found by a simple DP.
Thanks a lot !!!
I had the same question, but I'm not sure I understand the above answer.
Is there any way you could expand on this Xellos? Wont this solution only find paths for a single iteration of the maximum flow problem by finding some maximum C? I guess I'm not understanding how you handle cases where leaving more in the residual graph will allow for an overall higher maximum.
The idea of a dynamic programming solution makes sense to me, but it seems like we would still end up with a hefty exponential time (although probably improved from factorial) runtime. Any elaboration would be greatly appreciated.
Thank you.
Once you know the value of the max flow, i.e. c, as Xellos pointed out, you can calculate the number of paths from source to sink by DP. You remove all the edges with capacity < c from the graph as they can't be on a path that provides max flow. Now, to calculate the number of paths, you can first topologically sort the graph (it's a DAG, so it's possible) and then compute the dp values in the topologically sorted order. DP[source] = 1. For all others,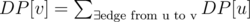 .
.
Correct me if I am wrong.