Is this problem solvable with some data structure or some other idea is required?

You have M sets of N-bit strings, numbered from 1 to M, and all of them are initially empty. Then, you have Q operations of the following kind: add to the i-th set, all the N-bit strings with the k-th bit equal to b. You must output the number of N-bit strings in the set consisting of the intersection of all the M sets after adding all the strings.

Input

The first line of input consists of 3 positive integers: M (2 ≤ M ≤ 100000), N (1 ≤ N ≤ 10000) and Q (0 ≤ Q ≤ 100000). The next Q lines consists each of 3 integers: i (1 ≤ i ≤ M), k (0 ≤ k < N) and b (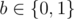), representing the operation described above in the statement.

Output

One line with one integer. The number of strings in the intersection of the M sets after all the operations. It is guaranteed that the answer will fit in a 32 bit signed integer.

Example input

3 3 3
1 0 1
3 2 1
2 1 0

Example output

1

Explanation

There are 3 initial empty sets of 3-bit strings. There are 3 operations. The first one adds to the first set all the strings with the bit 0 equal to 1. The second one adds to the third set all the strings with the bit 2 equal to 1. The third one adds to the second set all the strings with the bit 1 equal to 0. So, after all the operations, the sets consists of the following strings:

1) {100, 101, 110, 111}

2) {000, 001, 100, 101}

3) {001, 011, 101, 111}

The intersection of the 3 sets is the set {101}, so the answer is 1.

Thanks!