Теперь разбор завершен.
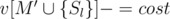
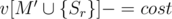
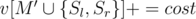
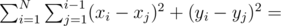
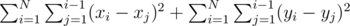
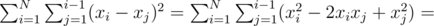
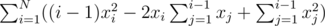
Задача A: Подарок (Роман Едемский)
Предположим, что оптимальным решением является пара (A, B), где A - количество золотых монет в подарке, а B - количество серебряных монет. Нетрудно заметить, что существуют такие 2 индекса i и j (возможно совпадающих), что gi = A и sj = B, так как в противном случае мы бы могли уменьшить A или B, не нарушив связность графа.
Обозначим через R(A,B) граф, в котором для всех i выполняется gi ≤ A и si ≤ B.
Обозначим через T(A) взвешенный граф, в котором для всех ребер выполняется ограничение gi ≤ A, а весами ребер будут si. Найдем в этом графе остовное дерево, у которого максимальное ребро - минимальное возможное. Можно показать, что для данного фиксированного A наименьшим значением B, при котором граф R(A, B) все еще связный, как раз будет это значение максимального ребра.
Утверждение. Минимальный остов графа одновременно является остовом, у которого максимальное ребро - минимальное возможное.
Доказательство. Рассмотрим любой минимальный остов L. Если существует остов P, у которого все ребра имеют строго меньший вес, чем вес максимального ребра у L. Тогда мы могли бы удалить из L макс. ребро и заменить его каким-то ребром из P, тем самым уменьшив его вес. Поскольку L - минимальный остов, мы не можем уменьшить его вес, следовательно такого P не существует.
Отсортируем все ребра исходного графа по возрастанию gi. Переберем все возможные значения A среди gi. Тогда ребрами графа T(A) для фиксированного i будут все ребра с индексами j ≤ i. Осталось научиться быстро находить мин. остов в этом графе.
Предположим, что мы для какого-то i нашли мин. остов в графе T(gi) (в случае, если граф несвязный, то в каждой его компоненте связности найден мин. остов). Добавим в него i + 1-е ребро. Если это ребро соединяет разные компоненты связности, просто добавим его, в противном случае в дереве образуется ровно один цикл. Найдем в нем максимальное ребро и удалим его из графа, получив таким образом новый минимальный остов в компоненте, куда добавилось ребро (доказательство опускается).
Поиск максимального ребра в цикле на дереве можно осуществить за O(N), а весь алгоритм будет работать за O(NM + MlogM).
Задача B: Мыши и сыр (Роман Ризванов)
Легко заметить, что количество ближайших кусков сыра для каждой мыши не превышает 2.
Найдем для каждой мыши ближайший сыр слева и справа. Из двух направлений выберем то, которое дает более короткий путь или оба, если длины путей одинаковы. Если на выбранном пути между мышью и сыром есть другая мышь, то мы это направление изымаем из рассмотрения, так как другая мышь быстрее съест тот сыр. Теперь все направления мышей непосредственно ведут к сыру и к каждому куску сыра ведет не более одного направления с каждой стороны.
Будем обрабатывать мышей слева направо. Если очередная мышь может двигаться влево и сыр слева не выбрала никакая из уже рассмотреных мышей или этот сыр выбрала мышь с таким же расстоянием до сыра, то текущая мышь двигаясь влево успеет поесть сыр, не мешая остальным мышам. Так как к сыру ведет не более одного направления, то этот выбор не повлияет на следующих мышей, а поэтому и не может в дальнейшем ухудшить ответ. В остальных случаях, двигаясь влево мы не сможем улучшить ответ, поэтому если мышь может двигаться вправо, то это единственная возможность для этой мыши поесть сыра, поэтому она выбирает движение вправо. Если мышь не может двигаться вправо, то она никак не сможит улучшить ответ.
Сложность решения O(N + M).
Также существует решение этой задачи при помощи динамического программирования.
Задача C: Мутация (Ярослав Твердохлеб)
В разборе вместо терминов "риск", "геном" и "ген" будут использоваться термины "стоимость", "строка" и "символ". Обозначим начальную строку через S.
Обозначим через M битовую маску символов, которые будут удалены. Переберем все возможные M. Для фиксированного M найдем стоимость строки, которая получилась и если она не превышает T - увеличим ответ на 1. Реализация этого алгоритма "в лоб" работает за O(2KN).
Избавиться от перебора нам не удастся, поэтому будем улучшать нахождение стоимости строки для фиксированного M.
Рассмотрим некоторую пару индексов символов из начальной строки l и r. Обозначим через M' битовую маску всех символов, которые лежат строго между ними. Если 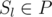 или
или 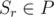 , то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного l возможных положений для r может быть не больше, чем K. Значит, всего таких пар O(NK). Определим, какой вид должно иметь множество M, чтобы после его удаления эти позиции оказались рядом? Нетрудно заметить, что для этого должны выполняться такие 2 условия:
, то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного l возможных положений для r может быть не больше, чем K. Значит, всего таких пар O(NK). Определим, какой вид должно иметь множество M, чтобы после его удаления эти позиции оказались рядом? Нетрудно заметить, что для этого должны выполняться такие 2 условия:
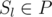 или
или 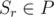 , то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного l возможных положений для r может быть не больше, чем K. Значит, всего таких пар O(NK). Определим, какой вид должно иметь множество M, чтобы после его удаления эти позиции оказались рядом? Нетрудно заметить, что для этого должны выполняться такие 2 условия:
, то, очевидно, эти позиции рядом никогда не будут. Отсюда можно сделать вывод, что для фиксированного l возможных положений для r может быть не больше, чем K. Значит, всего таких пар O(NK). Определим, какой вид должно иметь множество M, чтобы после его удаления эти позиции оказались рядом? Нетрудно заметить, что для этого должны выполняться такие 2 условия:1. 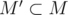
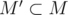
2. 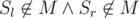
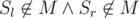
Переберем все допустимые пары l и r, для каждой найдем M'. Попутно для каждой тройки (a,b,P) будем хранить сумму стоимостей соседства всех пар l и r, для которых Sl = a, Sr = b, M' = P. После этого для фиксированного M переберем все пары символов (a, b), а так же подмножества P и просуммируем стоимости, которые мы сохранили. Прибавим к этому стоимость выбрасывания символов из M и получим конечную стоимость строки. Сложность решения O(3K * K2 + NK).
Попробуем улучшить предыдущее решение, засчет уменьшения множителя при 3K. Рассмотрим такой (неправильный) алгоритм:
Переберем все допустимые пары l и r и для каждой найдем M'. Заведем массив v, в котором для каждой маски P будем хранить сумму стоимостей соседства для всех пар l и r, для которых M' = P. Для фиксированного M найдем сумму значений из v по всем подмаскам M, прибавим к ней стоимость удаления M и получим конечную стоимость строки.
Этот алгоритм не является правильным, так как некоторые стоимости соседства мы прибавим к суммарной стоимости, но на самом деле позиции не будут соседями, т.к. один из концов (или оба сразу) будут принадлежать M, т.е. будут удалены. Воспользуемся формулой включения-исключения и при заполнении массива v сделаем следующие действия:
v[M'] + = cost
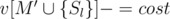
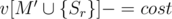
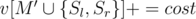
При таком заполнении v описанный выше алгоритм будет работать правильно и сложность станет O(3K + NK).
Этого все еще недостаточно, но мы уже почти у цели. Осталось научиться быстро считать сумму в массиве v по всем подмаскам M. Для этого рассмотрим следующий итеративный алгоритм:
Пусть перед первой итерацией у нас есть массив v, в котором хранятся начальные значения. После итерации с номером i в v[mask] будет храниться сумма значений из изначального массива v по всем подмаскам mask, для которых первые K - i бит совпадают с соответствующими битами маски mask. На итерации с номером i для всех масок, в которых i-й бит (нумерация с единицы) единичный сделаем сделаем такое: v[mask] + = v[mask\{i}]. Нетрудно заметить, что после выполнения K итераций этого алгоритма в новом массиве v как раз и будут находиться суммы по всем подмаскам из изначального массива v.
Сложность алгоритма O(2KK + NK).
Задача D: Плюс и XOR (Даниил Нейтер)
Рассмотрим какой-то единичный бит в X. Если соответствующий бит в Y равен 0, то мы можем их поменять местами, уменьшив X и увеличив Y. При этом их сумма и xor не изменятся. Отсюда можно сделать вывод, что если какой-то бит равен единице в X то он будет равен единице и в Y. Отсюда Y = X + B. Учитывая, что X + Y = X + X + B = A, получаем следующие формулы для нахождения X и Y:
X = (A - B) / 2
Y = X + B
Следует также учесть, что если выполняется хотя бы один из следующих пунктов:
- A < B
- A и B имеют разную четность
- X and (A - X) ≠ X, где and - побитовое "и"
то ответа не существует и следует вывести -1.
Задача E: Точки (Даниил Нейтер)
Если перегруппировать слагаемые, то можно разбить сумму на две:
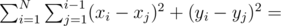
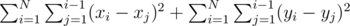
Рассмотрим подсчет суммы по иксам:
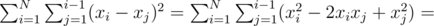
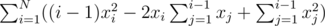
Полученная формула позволяет посчитать ответ за 1 проход. Сложность решения O(N).
Задача F: Турист (Илья Порублев)
Из события i можно попасть в событие j, если выполняются условия:
- ti ≤ tj
- |xi - xj| ≤ |ti - tj|· V
Если события представлять в виде точек на координатной плоскости с координатами (xi, ti), то предыдущие 2 условия можно представить графически, а именно:
Из события i можно попасть в событие j, если точка (xj, tj) лежит внутри угла направленного вверх с вершиной в (xi, ti), а стороны которого образуют угол arctg(V) с вертикалью. Сделаем преобразование координат, при котором точка с координатами (xi, ti) переходит в точку (pi, qi), где
pi = - xi + ti * V
qi = xi + ti * V
Тогда условие того что из события i можно попасть в событие j принимает вид: pi ≤ pj и qi ≤ qj. Отсортируем все точки по возрастанию координаты p, а при равном p - по возрастанию q. Задача (та часть, где можно самому выбирать стартовую точку) сводится к тому, чтобы в получившемся массиве найти самую длинную возрастающую подпоследовательность по q. Это можно сделать за O(NlogN).
Чтобы решить часть, в которой турист стартует из точки (0, 0) можно создать фиктивное событие со временем 0 и абсциссой 0 (если такого еще небыло) и потребовать чтобы мы обязательно посетили его первым.
Суммарная сложность решения O(NlogN).











Совершенно непонятно что имеется ввиду.
Пусть dp[i][j] = минимальному префиксу X (я перевернул числа, то есть идем от младшего бита), что есть префикс Y, что X + Y = A, X ^ Y = B (тоже префиксы A и B). При этом j - это есть перенос разряда в сумме или нет.
Ну и ответ на задачу будет лежать в dp[64][0], а Y = A - dp[64][0].
По задаче D есть несколько интересных тестов, например : 7 3
Ваше решение X=(A-B)/2 и т д должно дать ответы 2 и 5, но если их проксорить то они не дадут вам 3 . Вот вам и тестирующая система (сам сдал эту задачу с точно таким же алгоритмом).
Если xor чисел = 1 , то очевидно, что на таком разряде бит в одном числе 1 в другом 0, так как мы минимизируем 1е число , то ставим этот бит во второе число. Расставим полностью все биты для которых xor = 1. Теперь у нас остались только биты xor которых = 0, то есть они должны быть равными. Переведем число которое получилось после первого перехода и отнимем его от нужной суммы, пускай это будет ost. Зная что 2i>2i-1+2i-2+...1 получаем жадность, идем по битам , если xor равен 0 и 2i+1 <= ost то ставим на этот разряд в оба числа 1 иначе 0.
Вопрос по А. А как добавлять/удалять ребра из остова за O(1)?Но на самом деле хочется это уметь за log в какой-то степени от N.
Задачу B можно было также решать динамическим программированием - кода чуть побольше, зато думать поменьше. Я написал рекурсию с запоминанием, состояние - номер текущей мыши, последний кусок сыра, который кто-то ел до этого и количество мышей его евших.
Задачу E при заданных ограничениях можно было сдать за квадрат. Ведь различных координат всего 20001 (по x и по y). Можно было завести массив, где сказано, сколько точек с заданной координатой и в лоб посчитать ответ.
I would like to ask about problem F. Is there a particular reason why you sort by p first before you sort by q? If not, will sorting by q and then by p for tiebreak change the solution? If not, may I know if you can prove so? I can understand how you make the transformation and why the transformation is correct, but I am not convinced that you can get the optimal solution just by sorting and finding the LIS (Do you mean the longest non-decreasing subsequence? From what I understand, I think you first label the vertices according to the time when they appear. If they appear at the same time, then they have the same label.) Can you please give a proof or explanation why it works?
Thanks in advance!
Hi,
Now we can get to the event j from the event i if pi ≤ pj и qi ≤ qj. Let's sort all points in ascending order of p. If several points have the same p we will sort them by q.Can you please explain it for me?What do you want to be explained? Why "Now we can get to the event j from the event i if pi ≤ pj и qi ≤ qj."? Or what "If several points have the same p we will sort them by q." mean? Or what?
Here is more detailed tutorial. It's in Ukrainian, but you can Google-translate it (result is poor, but some things are still correct) and look at figures and equations.
I CAN try to reply on more concrete questions, but I don't want to translate the whole text...
Well, What are the significances of p, q axes and angle arctg(v)? What do they represent?
What I understand before, as I mentioned in another comment's reply was as below: to go to j from i:
abs(xj - xi) / tj - ti <= vso,xj + v*tj >= xi + ti*vand-xi + v*ti >= -xj + v*tAxis $$$p$$$ is the direction, where the tourist moves (in plane $$$(x,t)$$$), if his speed is ($$${-}v$$$), i.e.maximal by absolute value and directed to left. Its positive ray is the left-bottom border of the area where the tourist can get in time, starting from the origin of the $$$(p,q)$$$ coordiante system. Similarly, $$$q$$$ is the direction, where the tourist moves (in plane $$$(x,t)$$$), if his speed is ($$${+}v$$$), i.e. maximal by absolute value and directed to right; its positive ray is the right-bottom border of the area where the tourist can get in time, starting from the origin of the $$$(p,q)$$$ coordiante system.
It's not very obvious to look at these axes... But, from other hand, it's not unnatural: we need some effective checking of where the tourist can get in time and where he cannot, so let's try: what, if we'll consider borders of the "reachable-in-time" area as coordinate axes?
I hope this is my last query:
If tourist needs to go from i to j where xi > xj, that time the velocity is negative. Right? And, the velocity can not be positive and negative at a time,
But why do we check
Why not
The axis directed from bottom to top is $$$t$$$ (time). The tourist cannot travel in time as he wants and/or change time flow direction. All what he can is to choose
whether to stay at place with zero velocity (= move in direction of $$$t$$$, which is exactly in the middle between positive direction of $$$p$$$ and positive direction of $$$q$$$);
or to move with velocity ($$$-v$$$), negative and maximal by absolute value, which is exactly positive direction of $$$p$$$;
or to move with velocity ($$$+v$$$), positive and maximal by absolute value, which is exactly positive direction of $$$q$$$;
or to move with velocity $$$0<w<v$$$ (where $$$v$$$ is $$$v$$$ from input data, and $$$w$$$ is actual tourist's velocity), which is in the same quadrant of the $$$(p,q)$$$-system (both $$$p$$$ and $$$q$$$ positive), but $$$q$$$-projection is bigger that $$$p$$$-projection; in other words, $$$0<w<v$$$ corresponds to $$$0<p<q$$$;
or to move with velocity $$$-v<w<0$$$ (where $$$v$$$ is $$$v$$$ from input data, and $$$w$$$ is actual tourist's velocity), which is in the same quadrant of the $$$(p,q)$$$-system (both $$$p$$$ and $$$q$$$ positive), but $$$q$$$-projection is smaller that $$$p$$$-projection; in other words, $$$-v<w<0$$$ corresponds to $$$0<q<p$$$;
Whereas $$$(q_i > q_j)$$$ (for moving from $$$i$$$ to $$$j$$$) requires either moving with speed $$$w$$$ which is $$$-\infty\leq w < -v$$$, or even moving in reverse direction of time. Similarly, $$$(p_i > p_j)$$$ (for moving from $$$i$$$ to $$$j$$$) requires either moving with speed $$$w$$$ which is $$$v<w\leq\infty$$$, or even moving in reverse direction of time. So, it's required to have both $$$(p_i\leq p_j)$$$ and $$$(q_i\leq q_j)$$$
i dont understand the transformation of (xi,ti), how does it work??? can anyone tell me the answer?
What is "P"?
It seems that "P" hasn't been metioned before.
I really cannot understand this sentence.
And may "absiously" means "abviously"?
Problem D is right?
I doubts it, for expleam, A=14 and B=4
then X=(14-4)/2=5 Y=5+4=9
and A>B and A and B have some parity and A-X=Y
but X^Y=5^9=12
This is my doubts. And I think (A-B)/2=X&Y .
But I don't know the specific X and Y values
and is &
But I saw many wrong program still through the test,
and thank you very much for your patience solutions
Can someone explain the question Gift in this question it is asking for the minimum coins such that every road's gold coin and silver coin constraints are satisfied then if (A,B) is a valid solution then we can make A=infinite and B=infinite so that there will be always a solution also won't A=max(all gi's) and B=max(all si's ) where gi=minimum gold coins for ith road and si=minimum silver coins for ith road (this is what i have understood from the question can anyone tell what's wrong in my understanding )?
Problem D has weak testcases. My solution gets AC despite giving an incorrect answer on the testcase '10 6'.
Shit. This was 8 years ago.
How to solve A without MST??
Let us consider two cities $$$a$$$ and $$$b$$$. We use dfs to calculate the minimum amount of tugriks required for travelling from $$$a$$$ to $$$b$$$. And the answer will be maximum of such value among all pairs of cities.
The problem is, I think that calculation of this value requires to use Dynamic Programming. Any hints on that??