Блог пользователя NeverSayNever

How to solve this problem from codeforces ?
Автор NeverSayNever, 10 лет назад, По-английски

Problem Name : Cinema Problem Link : http://codeforces.me/contest/200/problem/A Tutorial Link : http://codeforces.me/blog/entry/4769

I am trying on this problem but not able to come with an idea. I thought of decomposing this |x2-x1| + |y2-y2| but that does not work in this case as we need to find the nearest coordinate not the farthest one.

I saw some simple short solution for this problem but not able to get any of those solutions. Please help me.

Any kind of help will be appreciated. :)

  • Проголосовать: нравится
  • +7
  • Проголосовать: не нравится

»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Can anyone help me with this problem or not ?

→ Ответить
  • »
    »
    10 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Its not the same idea with editorial but i think it is solvable with a segment tree. I will explain it if it works after my coding.

    EDT: No it doesnt working B(

    → Ответить
»
10 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

i am not able to understand what is mentioned in the editorial.

→ Ответить
»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

What part of the tutorial do you find difficult to understand?

As far as I understand the main ideas of the solution is the following.

  • For each cell (r, c) maintain the values left[r][c] and right[r][c], where the first value gives the nearest free cell to the left of (r, c) in the same row (i.e. r) and analogously for the second value and right.

  • When we get a query (a, b) and that cell is already occupied, loop through all rows in the range [a - d...a...a + d] in order of increasing distance from a, while maintaining the best answer x found so far. Break this loop when d > x.

  • When you process a row i, you can find the cell in that row closest to (a, b) in O(1) time by choosing min(left[i][b], right[i][b]).

  • The complexity of a query is in other words O(d), so how large can d get before d > x? Consider the case when all queries ask for (a, b), since this is the worst case that will maximize x. In this case all occupied seats will be centered around (a, b) in a diamond square shape. The area of this diamond is obviously at most k, and its sides is thus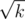 and thus the diagonal/height of the shape is less than 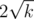. I.e. when we have reached a row i with distance 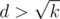from row a, we will already have found an answer x such that x < d, and thus we can give a 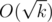bound for each query.

  • However, what if the matrix is too narrow (e.g. m = 3)? Then the diamond shape won't fit and our reasoning about the complexity doesn't hold, and that would mean that we would have to process a lot of rows! But despair not! Look what happens if we rotate the matrix 90 degrees (so if n > m rotate the matrix)! Now we have very few rows (e.g. n = 3) and this works to our advantage! This case is actually better for us than the case when the whole diamond shape fits, and our reasoning about the complexity once again holds.

  • So now we have found our answer (u, v) for the query (a, b), but now we must update left and right for some values in row u. How can we do this efficiently? The tutorial seems to suggest that we use DSU for this, but actually we don't need any additional data structure to update left and right efficiently (it suffices that we use DSU inspired ideas when we look at e.g. left[i][b]). I'll leave this as an exercise for you. ;)

→ Ответить
  • »
    »
    10 лет назад, # ^ |
    ← Rev. 2   Проголосовать: нравится 0 Проголосовать: не нравится

    Thanks Klein ,

    I just solved this problem with the understanding of editorial but not able to convince myself about the complexity of the solution but yes you made it very very clear to me. Thanks once again :)

    Yes. you are right we do not need any additional data structure like DSU to update left , right . i just simulate that row again with little optimisation and it worked :) but complexity in my case is O(K*(sqrt(K)+M)) in worst case .

    → Ответить
    • »
      »
      »
      10 лет назад, # ^ |
      ← Rev. 3   Проголосовать: нравится 0 Проголосовать: не нравится

      Just do it like this and you'll get . =)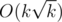

      int findNextLeft(int r, int c)
{
    if(cell[r][c] is empty) return c;
    if(left[r][c]==INF) return INF; //We define left[r][0] as INF.
    return left[r][c] = findNextLeft(r, left[r][c]);
}

      This may look daunting, since some query may take O(k) time. But in order to increase the number of calls/iterations of the function findNextLeft(r, c) you must occupy a cell in that row (i.e. r), and each cell increase the number of calls/iterations by at most 1. And because the number of cells that we will occupy throughout the whole program is k, the total amortized running time of findNextLeft is O(k).

      → Ответить