This is my version of the editorial for problem D of Codeforces Round 973 (Div. 2). It was motivated by GrishinD's great blog about his solution and presents a slower yet interesting alternative. I wanted to try this exercise to improve my thinking process and maybe become a div1 codeforcer along with GrishinD !
I first had a dynamic programming approach and got TL. Then I tried to work with binary search. I used a constructive algorithm inside the search to check for the validity of the current value. My solution got AC but I wasn't convinced by the correction and I wanted to understand in depth.
This blog explains my solution and brings a comprehensive proof. I'll first describe my algorithm and intuition, and then go through the proof.
Statement
Your are given an array $$$a_1,a_2,…,a_n$$$ of the length n
You can perform any number (possibly, zero) of operations on the array.
In one operation, we choose a position $$$i (1 \leq i \leq n-1)$$$ and perform the following actions:
- $$$a_i:=a_i-1$$$,
- $$$a_{i+1}:=a_{i+1}+1$$$
Find the minimum possible value of $$$max(a_1,a_2,…,a_n)-min(a_1,a_2,…,a_n)$$$
I — Notation and vocabulary
I will use some notations I found useful.
- $$$\forall i, 1 \leq i \leq n$$$ I will denote $$$a_i$$$ as $$$a[i]$$$.
- $$$max(a) $$$ and $$$min(a)$$$ will denote respectively $$$max_{i \in [1, n]}{a[i]}$$$ and $$$min_{i \in [1, n]}{a[i]}$$$
I had a pretty mathematical approach, but I will describe the problem as a line of columns of blocks of size $$$a[i]$$$.
II — Constructive algorithm and intuition
The solution first shows that the smallest maximum (denoted $$$alpha$$$) and the largest minimum obtainable (denoted $$$beta$$$) can be found with binary search in $$$\mathcal{O}(n*log(n))$$$. Then I bring the proof that these two values can be obtained simultaneously using the operation.
I'll describe here my first algorithm used in the binary search to check whether $$$alpha$$$ can be larger than all values of a rearranged $$$a$$$ array.
For $$$i=1$$$ to $$$i=n-1$$$, if $$$a[i] > alpha$$$:
- $$$a[i] := alpha$$$
- $$$a[i+1] := a[i+1] + alpha - a[i]$$$
Note that it is alway a valid algorithm, since it can be decomposed in separation application of the operation.
Visually, the algorithm go through columns from left to right. If a column exceeds $$$alpha$$$, the excedent is reported to the next column.
Let's start with an input array $$$a$$$. The first column excedent is reported to the next, and so on.

Eventually we reach the end of the array

At the end of the loop, $$$alpha$$$ is an admissible majorant iff the last column doesn't exceed $$$alpha$$$. In this case, $$$alpha$$$ is too low, it can't be the smallest minimum.
The same logic can be applied to show that $$$beta$$$ can be the smaller than all values of a rearranged array with the following algorithm
For $$$i=n$$$ to $$$i=2$$$, if $$$a[i] < beta$$$:
- $$$a[i] := beta$$$
- $$$a[i-1] := a[i-1] - (beta - a[i])$$$
Starting from another input array $$$a$$$, the propagation goes backwards :
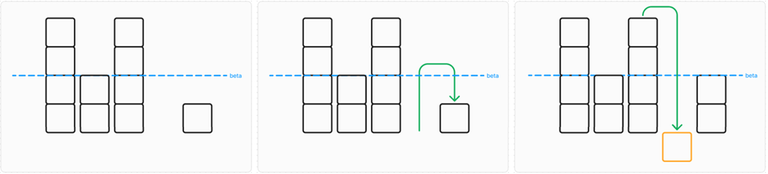
Values in $$$a$$$ can be temporarly negative as shawn in orange, only the value of $$$a[0]$$$ needs to be tested.

At the end of the loop, $$$beta$$$ is an admissible minorant iff the first column is greater or equal than $$$beta$$$. In this case, $$$beta$$$ is can be an admissible minorant.
The proof is similar.
The intuition is then that we can apply the $$$alpha$$$-algorithm and then the $$$beta$$$-algorithm to get a rearranged array with the smallest maximum $$$alpha$$$ and the largest minimum $$$beta$$$. Then the solution of the problem is $$$alpha - beta$$$.
It seemed logical at first, but I couldn't be sure of its validity. I took some time to think, and the rest of the blog is a formal proof of this result. Time for the heavy guns.
III — Formal proof of $$$alpha$$$-$$$beta$$$
Previous parts showed that we can find $$$alpha$$$ and $$$beta$$$ with a constructive algorithm starting from the initial array $$$a$$$. The idea of the proof is to show that applying $$$alpha$$$-algorithm yields an array for which it is alway possible to apply $$$beta$$$-algorithm as well.
A — Characterization of admissible maximum and minimum
The first step is to find $$$beta= max(min(\tilde{a}))$$$, where $$$\tilde{a}$$$ is the input array after performing an arbitrary number of operations. This is the largest value that can be obtained for the minimum value in the array $$$a$$$.
For a value $$$beta$$$ to be an admissible minimum of $$$\tilde{a}$$$ is equivalent to this statement : $$$\forall i, 1 \leq i \leq n, \sum_{j=1}^{j=i}{a[j]} \geq i * beta$$$
In other words, the following statements are equivalent
For any position $$$i$$$, the total amount of blocks left to this position must possible to be less or equal to $$$i$$$ columns of size $$$beta$$$.
The columns $$$1$$$ to $$$i$$$ can be rearranged using the operation to be all greater than $$$beta$$$.
Proof
(Note that this applies to the prefix of size $$$k$$$ of $$$\tilde{a}$$$.)
Initialisation
- For $$$k=1$$$, the statement is obvious.
- For $$$k=2$$$, the first column alone has to be larger than i, because it can't ever grow. The second can be smaller, as long as there is enough in a[1]. This writes as : $$$a[1] \geq beta$$$ and $$$a[2] + (a[1] - beta) \geq beta$$$, which is equivalent to $$$(H_2)$$$.
Induction
Suppose $$$(H_k)$$$ is true for an arbitrary value of $$$k$$$. Let's show that $$$(H_{k+1})$$$ is true.
$$$[A \Leftarrow B]$$$ Suppose the right part of $$$(H_{k+1})$$$. If $$$\sum_{j=1}^{j=k+1}a[j] < (k+1)*beta$$$, there is simply not enough blocks left from $$$k+1$$$ for $$$beta$$$ to be an admissible minimum. Therefore, reductio ad absurdum, $$$\sum_{j=1}^{j=k+1}a[j] \geq (k+1)*beta$$$ has to be true.
$$$[A \Rightarrow B]$$$ Suppose the left part of $$$(H_{k+1})$$$. By supposition, we can rearrange $$$a[1], ..., a[k]$$$ to be larger than $$$beta$$$. If $$$a[k+1] \geq beta$$$, the right part of $$$(H_{k+1})$$$ is true. Else,
$$$\sum_{j=1}^{j=k+1}{a[j]} \geq (k+1)*beta \iff \sum_{j=1}^{j=k+1}{a[j]} - k*beta \geq beta \iff \sum_{j=1}^{j=k}{a[j]} - k*beta \geq beta - a[k+1] \geq 0$$$
The sum $$$\sum_{j=1}^{j=k}{a[j]}$$$ represents the excedent left to $$$a[k+1]$$$ after rearranging $$$a[1], ... a[k]$$$ that can be used to get $$$\tilde{a}[k+1] \geq beta$$$
Conclusion
The two statements are equivalent. Moreover, there are also both equivalent to the statement "apply the $$$alpha$$$-algorithm yields a feasible solution". I won't write it again, but a symmetrical proof can be written to prove that the three following statements are equivalent :
$$$\forall i, 1 \leq i \leq n, \sum_{j=i}^{j=n}a[j] \leq (n-i+1)*alpha$$$
For any position $$$i$$$, the total amount of blocks right to this position must less or equal to $$$i$$$ columns of size $$$alpha$$$$$$alpha = max(\tilde{a})$$$
The columns $$$i$$$ to $$$n$$$ can be rearranged using the operation to be all lower than $$$alpha$$$The $$$alpha$$$-algorithm yields a valid array for which $$$alpha$$$ is a majorant.
The first interesting result is that this prefix (resp. suffix) sum can be used in the binary search for $$$beta$$$ (resp. $$$alpha$$$) instead of building a modified array. But the best is yet to come !
B — Use of smallest maximum and largest minimum in the solution
Finally, this last part shows that we can always rearrange initial $$$a$$$ into an array solution that has both $$$alpha$$$ as maximum and $$$beta$$$ as minimum.
With the optimal $$$alpha$$$ found with binary search and the suffix sum criterion, suppose that we apply $$$alpha$$$-algorithm to the input array $$$a$$$. We will show that it implies that the prefix sum criterion is still respected, and the $$$beta$$$-algorithm can always be applied as well.
$$$beta$$$ being the largest admissible minimum for a rearranged $$$a$$$, the prefix sum criterion is respected before applying $$$alpha$$$-algorithm.
We denote $$$a^{(k)}$$$ the state of the rearranged $$$a$$$ after applying the k-th step of the $$$alpha$$$-algorithm, i.e right after possibly modifying $$$a[k]$$$ and $$$a[k+1]$$$.
Initialisation
$$$(H_1)$$$ : after one step, $$$a^{(k)}[1]$$$ was either set to $$$alpha \geq beta$$$ or kept as $$$a[1] \geq beta$$$.
Induction
Suppose $$$(H_k)$$$ true for a fixed $$$k$$$. Consider $$$(H_{k+1})$$$ :
either $$$a^{(k)}[k+1] \leq alpha$$$ then $$$a^{(k+1)}[k+1] = a^{(k)}[k+1]$$$, and no blocks were moved after the column $$$k$$$. The prefix sum at index $$$k+1$$$ hasn't changed and the second part of $$$(H_{k+1})$$$ it true as well.
or $$$a^{(k)}[k+1] > alpha$$$, then $$$a^{(k+1)}[k+1] := alpha$$$ and $$$a^{(k+1)}[k+2] := a^{(k)}[k+2] + a^{(k)}[k+1] - alpha$$$.
By induction, $$$\sum_{j=1}^{j=k}a^{(k)}[j] \geq k*beta$$$ and $$$a^{(k+1)}[k+1] = alpha \geq beta$$$,
$$$\Rightarrow \sum_{j=1}^{j=k+1}a^{(k+1)}[j] \geq (k+1)*beta$$$.
Conclusion
$$$(H_n)$$$ is true, and the complete application of $$$alpha$$$-algorithm maintains the prefix-sum criterion, so $$$beta$$$ is still the largest minimum possible.
It is possible to search for $$$alpha$$$ and $$$beta$$$ separately, and combine them to build the final answer, $$$alpha-beta$$$.
Thank you for reading it so far, it took me much to much time, but I loved trying to formalize the proof. Let me know if you find mistakes, or simpler way of proving the result.
Thank you soullless for organizing this contest, and MikeMirzayanov for this great plateform. See ya !











Yay, let's go! Great post :)
When I saw your post, I was eager to share mine ! I also needed to justify my approach, because your solution is more efficient and really elegant, especially with the latest update
do we need to prove that $$$alpha$$$ is always greater than $$$beta$$$?
You're right, it is necessary, although I left it behind because it is straightforward.
$$$beta*n \leq \sum_{i=1}^{i=n}a[i] \leq alpha*n$$$, and $$$\sum_{i=1}^{i=n}a[i]$$$ never changes
Brilliant solution! You recieved an upvote :)
Brilliant solution! You recieved an upvote :)
That's crazy. I had the same approach but couldn't even conceive a proof
My two binary searches are actually the same thing. Given a value, if some a[i] exceeds it, it transfers all the remainder forward. Later I just check if all a[i] satisfy the condition. This always works because if I'm looking for the minimum then I can just set all the elements I can to be the minimum and end up with the last element bigger, but it doesn't matter because it's larger than the min. Also works for the maximum because if the current a[i] is greater than it I'll just transfer the remainder forward. Could probably use this to prove something in an easier manner maybe...