You are given an array S[1 . . . n] of real numbers, some positive and some negative.
Design an O(n log n)-time algorithm that determines whether S contains two elements S[i] and S[j] such that S[i] = −S[j]. The algorithm returns a “yes” if there is such a pair, and “no” otherwise. If the array S contains the element 0, then the algorithm always returns a “yes”.
Your algorithm has to be in-place (i.e. you can use only constant additional memory).
I solved it using Heap Sort, but is there any other solution? Because it is assumed that the student doesn't know Heap Sort yet.











sort and two pointers Lyova.
Yeah I did the same two-pointer thing! But what about the sorting part? which sort do you mean Sparlik? For example quick sort is O(n^2) in worst case. Merge Sort uses additional memory. (not in-place)
It is not assumed that the student must know Heap sort at this point of time.
That's why I am looking for an algorithmic solution (like a divide-and-conquer algorithm).
there is an in-place version of mergesort bitch.
Look on the Wiki page you mouse-faced faggot! https://en.wikipedia.org/wiki/Sorting_algorithm
Quicksort can be written in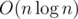 in the worst case since one can find a median in linear time.
in the worst case since one can find a median in linear time.
Could you please provide a link to an article where Quicksort is implemented in nlogn in the worst case. Because selecting random pivot takes O(1) and that's why algorithm runs in nlogn, if you waste N time to find the median, I believe the algorithm will run in O(n^2).
Google something like
linear time median.Quicksort runs in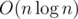 because in each step we do something in O(r - l) time and then call
because in each step we do something in O(r - l) time and then call
sort(l, mid)andsort(mid + 1, r)theremid~(l + r) / 2.So we can find median in O(r - l) time using algorithm which splits array into
n/5groups, for example.I made you my bitch!
Fuck Off.
it's for data structures with only
swapoperation allowed. However, we can use linked list in this problem. For linked lists, stable in-place merge algorithm is trivial.You cannot use additional memory like a linked list. (as I mentioned we are asked for an in-place algorithm)