In number theory, we always write a ≡ b (mod p) means that the reminder of division of a by p and the reminder of b by p are the same. Today, I have a question about this definition.
1. Same reminder of integers:
If 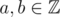 , a ≡ b (mod p) means
, a ≡ b (mod p) means 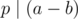 or
or 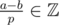 . It's quite easy to see that.
. It's quite easy to see that.
2. Same reminder of rational numbers:
We also write 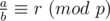 , for example:
, for example: 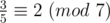 . What do they mean?
. What do they mean?
The above definition is obviously wrong, since 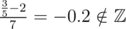 . But with the modular multiplicative inverse,
. But with the modular multiplicative inverse, 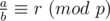 can be written as a * b - 1 ≡ r (mod p). So, in this case, I think the definition should be:
can be written as a * b - 1 ≡ r (mod p). So, in this case, I think the definition should be: 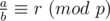 means: For every pair of integers (A, B) satisfies
means: For every pair of integers (A, B) satisfies 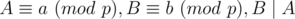 , we always have
, we always have 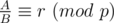 . Note that
. Note that 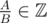 so we can use the definition for integers.
so we can use the definition for integers.
3. Same reminder of irrational numbers:
In the editorial of problem 446C - DZY любит числа Фибоначчи, the authors wrote:
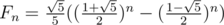
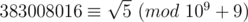
Fn ≡ 276601605(691504013n - 308495997n) (mod 109 + 9)
The correctness of the last equation can be proved easily. However, to get the final equation, we need some transform like: 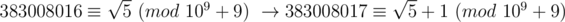 .
.
My question is, how can we define equations a ≡ b (mod p), when a or b is irretional number like that, and why the above transform is correct.
I'm looking forward to hearing your responses. Thank you for your help!
P/s: I know, this blog may have something difficult to be understood, but please do not vote down it. I have thought a lot about this problem, but I can't find the answer.











5^0.5 is a square root of x^2 = 5 (mod 1e9+9), you can calc it by wolframalpha.
From Wikipedia: For a positive integer n, two integers a and b are said to be congruent modulo n, and written as
a ≡ b (mod n)
if their difference a − b is an integer multiple of n (or n divides a − b).
How do you think about this?
That's the same thing.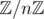 (with addition) is defined as the group of integers
(with addition) is defined as the group of integers 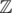 modulo the subgroup generated by n, namely
modulo the subgroup generated by n, namely 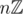 . And we have
. And we have 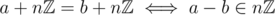
The above definition is only right in case a and b are integers. We can't use it in more general case.
I don't think it's possible or important to extend the definition of modulo on all irrational numbers. For example, how could you calculate π modulo 41?
Nevertheless, there is a useful technique called finding of discrete root. Its definition is quite simple.
Let's begin from the very beginning. Why can one divide the numbers modulo m? The result can be not an integer. Though if we invent a good definition for division modulo m, it will help us a lot further.
Let's make it this way: if
if 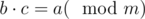 . One can simply look that such a definition doesn't take us out of integers and has all the properties normal division has.
. One can simply look that such a definition doesn't take us out of integers and has all the properties normal division has.
What about the square (or some other) root? Let's make a definition: if
if 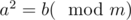 .
.
Now you can use the definition above to find the integer roots modulo m. For example, you can check this property for 383008016 you mentioned in post.
It would be consistent to define the equivalence class of π in this scenario as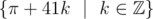 , although the question remains whether that is actually a useful tool to have. As far as finding a representative in the range [0, 41) is concerned, the
, although the question remains whether that is actually a useful tool to have. As far as finding a representative in the range [0, 41) is concerned, the
fmodfunction provides an implementationAlso your definition of a square root cannot really work like that. It assumes that there is only one such a, but that might not the case, e.g.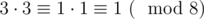
The thing is that every integer number that satisfies our definition should also satisfy all our requirements. This is some quality measure of a good definition.
So you're defining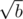 as a set? That is however inconsistent with the definition for real numbers, where it is a concrete value (the positive one that fulfills the condition).
as a set? That is however inconsistent with the definition for real numbers, where it is a concrete value (the positive one that fulfills the condition).
In fact, every number according to modular arithmetic is a set of numbers. 1 modulo 41 is a set of {...-81,-40,1,42,83...}. And yes, this really differs the modular arithmetic from the common one.
But I think one should not be feared of the sets of numbers when every number from such set has a property essential for us.
I agree with you that we don't need to make definition of modulo on all irrational numbers. But if we write a ≡ b (mod p) with some irrational number a, we should make definition about it.
Your definition for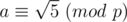 is ok. So how can you define the
is ok. So how can you define the 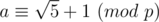 (I saw it in the editoral).
(I saw it in the editoral).
Recursively.
As now we can find the square root modulo m and we already know how to add modulo m we take some a which is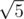 and add 1 modulo m.
and add 1 modulo m.
In fact, this works the same as in common math. When you first knew one can find square roots of every non-negative number you simultaneously knew that the result of the operation can be used in addition, subtraction etc.
I've been thinking about that exact editorial for quite a while and planned on writing the same question in a blog myself. You seem to know some about modular arithmetics so I hope you can answer me those two questions:
1) We can properly divide by modulo when it is prime, as otherwise the multiplicative inverse may not be unique and dividing is not really useful.
In the same way, to define sqrt(5) = 383 008 016 , does it mean that this is the only number which squared gives 5 modulo 10^9+9.
2) Edit: Ops, I guess I misread the editorial.
Thanks in advance! :)
1/ You should notice that, the number of x satisfies x2 ≡ b (mod p) is usually even, as x2 ≡ (p - x)2 (mod p). However, we can define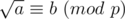 as: for every x satisfies x2 ≡ a (mod p), we always have x ≡ b (mod p) or x ≡ p - b (mod p). With this definition,
as: for every x satisfies x2 ≡ a (mod p), we always have x ≡ b (mod p) or x ≡ p - b (mod p). With this definition, 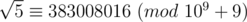 is correct. (And I think that's why the problem uses modulo 109 + 9 instead of 109 + 7 :D).
is correct. (And I think that's why the problem uses modulo 109 + 9 instead of 109 + 7 :D).
So are you saying that if we had used 616991993 instead, the answer would still be correct? I find that really counterintuitive :D
Ask your intuition a simple question: will the fibonacci formula become wrong if we take another number as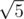 — especially,
— especially, 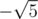 , as it also gives 5 when squared.
, as it also gives 5 when squared.
And then check the result manually :)
That's a very nice way to put it, thanks a lot :)