Apologize for my bad English.
We consider to make the answer with a fixed $$$x=2^{p_1}3^{p_2}5^{p_3}...$$$. It's $$$\displaystyle\prod^i C^{p_i}_{x+p_i-1} =\prod^i{\frac {x(x+1)(x+2)...(x+p_i-1)}{p_i!}}$$$ and is already proved in many editorials. Note that it's a polynomial of $$$x$$$, and it's highest exponent is no more than $$$\lfloor\log 2\times 10^5\rfloor = 16$$$.
To calculate the answer, we should know the value of $$$\displaystyle\sum_{i=0}^x i^d$$$. Actually, we have an equation:
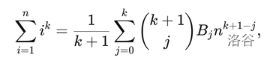
From Chinese OI-wiki, where $$$B_i$$$ stands for the i-th Bernoulli's Number.
Thus, we can solve the problem in $$$k\log^2 k$$$ time. Very slow, bro!
Code:











Auto comment: topic has been updated by Wind_Lyric (previous revision, new revision, compare).