Subsequences: they’re like the wardrobe combinations of coding—every possible way to arrange your elements without messing up the order. A subsequence is any sequence derived by deleting some (or no) elements of the array without changing the order of the remaining elements. This is my first blog on Codeforces ^-^ In this blog, I’ll guide you through the process of generating all subsequences of a given array using recursion. Along the way, we’ll explore the logic, implementation, and common pitfalls, with just the right mix of fun and formality.
What Are Subsequences?
A subsequence is any sequence derived from an array by deleting some (or no) elements, without changing the order of the remaining elements.
For example, given the array [1, 2, 3], the subsequences are: [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3] Notice how the order is preserved, and yes, the empty set [] is part of the deal—because sometimes doing nothing is a valid choice. :P
The Recursive Approach
Recursion is basically your lazy friend—it works by delegating smaller parts of the problem to itself. For subsequences, here’s the plan:
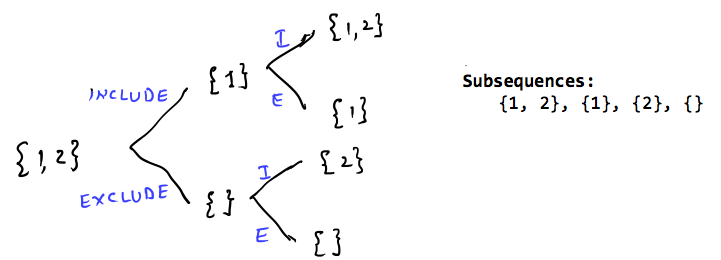
- At every index, you have two choices: — Pick the element: Include it in the current subsequence. — Don’t pick the element: Skip it and move forward.
- Keep repeating this until you’ve processed all elements.
- At the end, print (or store) the current subsequence.
Visualizing the Recursion Tree
For the array [1, 2, 3], the recursion tree looks like this:
[]
/ \
[1] []
/ \ / \
[1,2] [1] [2] []
/ \ / \ / \ / \
[1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] []
- At the root: Start with the empty set
[]. - First level: For each element, decide whether to pick or not pick it.
- Second level: Repeat the same decision for the next element.
- Third level: Continue until all elements are processed.
- Leaf nodes: Represent the final subsequences.
By the time the recursion is complete, you’ll have all possible subsequences.
Code Implementation
Here’s how to bring this concept to life with C++:
#include <iostream>
#include <vector>
using namespace std;
void generateSubsequences(int idx, int arr[], int n, vector<int> &ds) {
// Base case: If we’ve processed all elements
if (idx == n) {
if (ds.empty()) {
cout << "{}"; // Represent the empty subsequence
} else {
for (auto it : ds) {
cout << it << " ";
}
}
cout << endl;
return;
}
// Pick the current element
ds.push_back(arr[idx]);
generateSubsequences(idx + 1, arr, n, ds);
// Don’t pick the current element (backtrack)
ds.pop_back();
generateSubsequences(idx + 1, arr, n, ds);
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]); // Size of the array
vector<int> ds; // To store the current subsequence, we are passing this data structure (ds)
generateSubsequences(0, arr, n, ds);
return 0;
}
Feel free to share your thoughts or questions below. Happy coding! :D











I don't want to end up as rude but, how is this useful and isn't this trivial?
I suppose OP wants some contribution points.
it's basic coding of complete search, not something unique
world's most chatgpt blog ever
Even though people might find this as a "Basic" or "Anyone could have googled this" blog. But for me it kinda makes sense tho...
ofc it's not as advanced as you want to see in a CP website's blog. But you cant deny that content like this belongs to CF. (making CF more newbie friendly).
can this be modified for contiguous subsequences?
if you really want recursive approach go here, but it can be solved by using 3 nested loops
Why bro is sending GPT generated content as a Newbie?