Subsequences: they’re like the wardrobe combinations of coding—every possible way to arrange your elements without messing up the order. A subsequence is any sequence derived by deleting some (or no) elements of the array without changing the order of the remaining elements. This is my first blog on Codeforces ^-^ In this blog, I’ll guide you through the process of generating all subsequences of a given array using recursion. Along the way, we’ll explore the logic, implementation, and common pitfalls, with just the right mix of fun and formality.
What Are Subsequences?
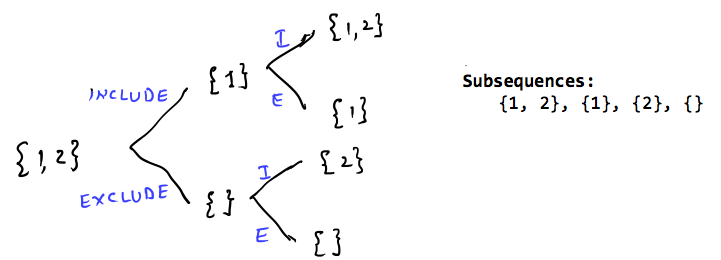
A subsequence is any sequence derived from an array by deleting some (or no) elements, without changing the order of the remaining elements.
For example, given the array [1, 2, 3], the subsequences are: [], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3] Notice how the order is preserved, and yes, the empty set [] is part of the deal—because sometimes doing nothing is a valid choice. :P
The Recursive Approach
Recursion is basically your lazy friend—it works by delegating smaller parts of the problem to itself. For subsequences, here’s the plan:
- At every index, you have two choices: — Pick the element: Include it in the current subsequence. — Don’t pick the element: Skip it and move forward.
- Keep repeating this until you’ve processed all elements.
- At the end, print (or store) the current subsequence.
Visualizing the Recursion Tree
For the array [1, 2, 3], the recursion tree looks like this:
[]
/ \
[1] []
/ \ / \
[1,2] [1] [2] []
/ \ / \ / \ / \
[1,2,3] [1,2] [1,3] [1] [2,3] [2] [3] []
- At the root: Start with the empty set
[]. - First level: For each element, decide whether to pick or not pick it.
- Second level: Repeat the same decision for the next element.
- Third level: Continue until all elements are processed.
- Leaf nodes: Represent the final subsequences.
By the time the recursion is complete, you’ll have all possible subsequences.
Code Implementation
Here’s how to bring this concept to life with C++:
#include <iostream>
#include <vector>
using namespace std;
void generateSubsequences(int idx, int arr[], int n, vector<int> &ds) {
// Base case: If we’ve processed all elements
if (idx == n) {
if (ds.empty()) {
cout << "{}"; // Represent the empty subsequence
} else {
for (auto it : ds) {
cout << it << " ";
}
}
cout << endl;
return;
}
// Pick the current element
ds.push_back(arr[idx]);
generateSubsequences(idx + 1, arr, n, ds);
// Don’t pick the current element (backtrack)
ds.pop_back();
generateSubsequences(idx + 1, arr, n, ds);
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]); // Size of the array
vector<int> ds; // To store the current subsequence, we are passing this data structure (ds)
generateSubsequences(0, arr, n, ds);
return 0;
}
Feel free to share your thoughts or questions below. Happy coding! :D










