I was shown this JOI problem by Jasonwei08 today. The problem statement boils down to:
Given an array $$$A$$$ of $$$2^L$$$ integers, $$$1 \leq L \leq 20$$$, process $$$1 \leq Q \leq 10^6$$$ queries. For each query, consisting of a length-$$$L$$$ pattern of either 0, 1, or ?, report the sum of all $$$A_j$$$ where the binary representation of $$$j$$$ matches the pattern.
For example, given the array $$$10, 2, 3, 15, 0, 9, 12, 3$$$, the query $$$?1?$$$ would match the binary indices $$$010, 011, 110, 111$$$, which are $$$2, 3, 6, 7$$$ in decimal. The result would be $$$A_2 + A_3 + A_6 + A_7 = 33$$$.
Let's start with a brute force approach. Build a perfect binary tree of all prefixes of length up to $$$L$$$, and traverse it downwards, summing the values at the leaves:
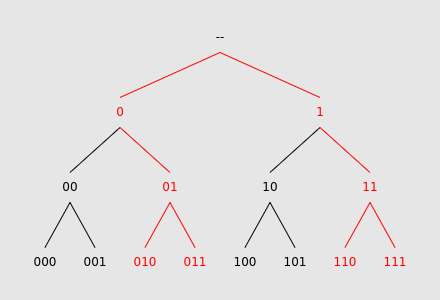
Notice that every time we "split", and take both children, the resulting subtrees are identical. We can use this to our advantage. Instead of subdividing into two separate searches, we can instead fold the two subtrees together, adding together the values at the leaves.
This optimization reduces the number of nodes traversed from $$$O(2^L)$$$ to $$$O(L)$$$, though processing each node isn't as simple anymore.
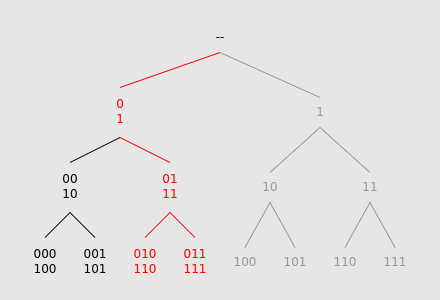
We can implement this by maintaining an initial array containing all of the values of the leaves, and at each tree-descent step, we create a new array by either:
- if we descend to only one child, cut the array in half and pick the appropriate side.
- if we split to both children, cut the array and overlay the two halves over each other, adding them together.
At the end, we obtain a length-one array whose only element is equal to the sum of all matching leaves.
This requires $$$O(2^L)$$$ space and time per search, which doesn't seem to be any better complexity-wise than brute force. However, we can now leverage another datastructure: a trie.
By building a trie out of all of the patterns, we can then run a downward search through the trie, at each step maintaining the array of remaining leaves. A depth-first search is ideal for this, as it guarantees that only one node at each depth can be processed at a time, and therefore provides a bound on memory usage.
Unfortunately, for this specific JOI task, the memory limit is too tight for a normal trie to work, even with very aggressive modifications. jay_jayjay suggested I sort and divide-and-conquer over the patterns as a sort of 'virtual trie', which worked!
(The intended approach to this task was in a very different direction, using SOS. Mine isn't even a very good one, I just thought the technique was cool.)
More generally, this works not only on binary strings, but on any pattern with a sufficiently low number of possible characters. It can also handle more complicated wildcards than ?, as long as subtrees can be efficiently folded together. However, it does require the full tree of strings to be stored in memory, limiting its applicability, unless some truly cursed sparse segtree magic happens...
That's about all for this weird little technique. I hadn't heard of it before, and neither had Jasonwei08, who seems to know every technique in existence, idk. So, I hope you enjoyed this, and maybe someday the perfect problem will come up where it can be used!











Thank you so much for sharing this technique with the community!!
Also, I do not know a lot of techniques, but I wish I do and I try to learn
Yayyyyy
nah I swear you know infinite techniques
i can confirm he does know infinite techniques, many more than me
orz idea, but how would you implement this? As in, how would you write a trie traversal that folds the tree?
Surprisingly, it wasn't very difficult. I stored $$$L+1$$$ arrays of size $$$2^L, 2^{L-1}, ...$$$, the biggest one initialized to $$$A$$$. Then, when depth-first searching the trie of queries, I cut/folded the current top-level array into the next one. So, $$$10,2,3,15,0,9,12,3$$$ would be left-cut into $$$10,2,3,15$$$, for example. Naturally at the deepest point of the dfs there would be a single value in the smallest array, and that would be the answer to the queries ending at that point in the trie.
Here's sort of what I mean:
It's a little confusing because the dfs in this situation is on the trie, not the binary sequences, which aren't represented in an explicit tree at all. The trie is traversed top-down, whereas the sequence tree is traversed bottom-up.
Also, I realize that 'folding' is a little misleading. It's more of an overlaying, as none of the children change order, as they might in a topological folding. I called it 'folding' because the way I was visualizing it was as if the leaves of the tree were a strip of paper and I were manipulating it to make different sections overlap.
Damn, that's smart as hell. So this entire trie traversal would end up being something like O(L*2^L) right?
Something like that. Theoretically if the trie traversal goes through every possible pattern, it works out to something like $$$2^L + 2^{L-1} \times 3 + 2^{L-2} \times 3^2 + \dots + 2 \times 3^{L-1} + 3^L$$$, because each node in the trie can have three children. But there is a bound on $$$Q$$$, the number of patterns, so I think we get something considerably closer to $$$L \times 2^L$$$.
Either way, it pretty comfortably passed under time limit. :P
Auto comment: topic has been updated by iframe_ (previous revision, new revision, compare).
This sounds like an abstracted version of SOS DP: https://codeforces.me/blog/entry/45223 Or maybe I am misunderstanding the difference.
I think I see what you mean — a pattern $$$P$$$ composed of
0s and?s will match all binary sequences that are a subset of the binary string $$$P'$$$ formed by replacing all the?in $$$P$$$ with1. So, SOS can be seen as sort of similar to my approach.However, in SOS we compute the subset sum of every sequence. In my case there were too many patterns to construct, and so the cut-and-fold approach intentionally only builds the patterns it needs to.
Also, cut-and-fold is theoretically able to support more complicated types of patterns. I don't believe SOS has an equivalent to patterns of
0,1, and wildcard?. An even more extreme example is sequences of decimal digits, where the characterEstands as a wildcard for any even digit, andOfor any odd digit. Maybe SOS can be adapted to support this; I'm not sure.Good connection, though! (And a helpful reminder that I should look more in-depth into SOS :p)
Yeah I think all of these things are things you can do through extension on SOS.
To handle wildcard, essentially we add a new "digit" to every position that depends on every other digit. This sort of transforms the original linear dependence in SOS dp to a tree
Normal: a -> b -> c
Now: a -> b and a -> c
Some very messy code that does this: (in base 3, 0 encodes wildcard, 1 is a '0', 2 is a '1'): ~~~~~ int div = 1; for(int i{}; i < n; ++i){ for(int m = amt-1; m >= 0; --m){ if((m/div)%3 == 0){ int lower = m — (m/div)*div; dp[m] += dp[(m/div + 1)*div + lower]; dp[m] += dp[(m/div + 2)*div + lower]; } } div *= 3; } ~~~~~
This idea that SOS dp works on trees of implications allows this to be used for the second example you also posed.
Theoretically, it could be used for dags?? but that would get very messy very quickly I think.
I think I see what you're getting at. If I'm understanding correctly, your code functions somewhat along the lines of this?
This is indeed fairly similar to the cut-and-fold approach, though it doesn't perform the folding step, and 'branches out' to every leaf instead.
When using SOS in this way, every possible DP state needs to be computed. In the task I was using cut-and-fold for, this requires storing $$$3^{20}$$$ states. Not only does this far exceed the memory limit, but the time limit as well.
Writing it as a memoized function can get around this but will add an extra log factor. This memory issue is precisely the reason why I fold together the tree instead of branching.
Processing a DAG shouldn't be that bad. I think you just need to ensure that each 'parent state' is processed before each 'child state', which can be achieved by arranging them in toposorted order, similarly to how you reordered the states
0,1,?such that the wildcard came first.I see I see, that makes sense. Thanks!
Auto comment: topic has been updated by iframe_ (previous revision, new revision, compare).
iframe orz
Jasonwei08 common orz moment
nou
iframe orz
nou
alter orz ifrm orz